stepcpncfamounts
Cash flow amounts and times for bonds and stepped coupons
Syntax
Description
Examples
This example generates stepped cash flows for three different bonds, all paying interest semiannually. The life span of the bonds is about 18–19 years each:
Bond A has two conversions, but the first one occurs on the settlement date and immediately expires.
Bond B has three conversions, with conversion dates exactly on the coupon dates.
Bond C has three conversions, with some conversion dates not on the coupon dates. It has the longest maturity. This case illustrates that only cash flows for full periods after conversion dates are affected, as illustrated here:
The following table illustrates the interest-rate characteristics of this bond portfolio.

Define the bond specifications.
Settle = datenum('02-Aug-1992'); ConvDates = [datenum('02-Aug-1992'), datenum('15-Jun-2003'),... nan; datenum('15-Jun-1997'), datenum('15-Jun-2001'),... datenum('15-Jun-2005'); datenum('14-Jun-1997'), datenum('14-Jun-2001'),... datenum('14-Jun-2005')]; Maturity = [datenum('15-Jun-2010'); datenum('15-Jun-2010'); datenum('15-Jun-2011')]; CouponRates = [0.075 0.08875 0.0925 nan; 0.075 0.08875 0.0925 0.1; 0.025 0.05 0.0750 0.1]; Basis = 1; Period = 2; EndMonthRule = 1; Face = 100;
Use stepcpncfamounts to compute cash flows and timings.
[CFlows, CDates, CTimes] = stepcpncfamounts(Settle, Maturity, ConvDates, CouponRates)
CFlows = 3×39
-1.1639 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 104.6250 NaN NaN
-0.9836 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.4375 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 4.6250 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 105.0000 NaN NaN
-0.3279 1.2500 1.2500 1.2500 1.2500 1.2500 1.2500 1.2500 1.2500 1.2500 2.5000 2.5000 2.5000 2.5000 2.5000 2.5000 2.5000 2.5000 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 3.7500 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 5.0000 105.0000
CDates = 3×39
727778 727913 728095 728278 728460 728643 728825 729008 729191 729374 729556 729739 729921 730104 730286 730469 730652 730835 731017 731200 731382 731565 731747 731930 732113 732296 732478 732661 732843 733026 733208 733391 733574 733757 733939 734122 734304 NaN NaN
727778 727913 728095 728278 728460 728643 728825 729008 729191 729374 729556 729739 729921 730104 730286 730469 730652 730835 731017 731200 731382 731565 731747 731930 732113 732296 732478 732661 732843 733026 733208 733391 733574 733757 733939 734122 734304 NaN NaN
727778 727913 728095 728278 728460 728643 728825 729008 729191 729374 729556 729739 729921 730104 730286 730469 730652 730835 731017 731200 731382 731565 731747 731930 732113 732296 732478 732661 732843 733026 733208 733391 733574 733757 733939 734122 734304 734487 734669
CTimes = 3×39
0 0.7377 1.7377 2.7377 3.7377 4.7377 5.7377 6.7377 7.7377 8.7377 9.7377 10.7377 11.7377 12.7377 13.7377 14.7377 15.7377 16.7377 17.7377 18.7377 19.7377 20.7377 21.7377 22.7377 23.7377 24.7377 25.7377 26.7377 27.7377 28.7377 29.7377 30.7377 31.7377 32.7377 33.7377 34.7377 35.7377 NaN NaN
0 0.7377 1.7377 2.7377 3.7377 4.7377 5.7377 6.7377 7.7377 8.7377 9.7377 10.7377 11.7377 12.7377 13.7377 14.7377 15.7377 16.7377 17.7377 18.7377 19.7377 20.7377 21.7377 22.7377 23.7377 24.7377 25.7377 26.7377 27.7377 28.7377 29.7377 30.7377 31.7377 32.7377 33.7377 34.7377 35.7377 NaN NaN
0 0.7377 1.7377 2.7377 3.7377 4.7377 5.7377 6.7377 7.7377 8.7377 9.7377 10.7377 11.7377 12.7377 13.7377 14.7377 15.7377 16.7377 17.7377 18.7377 19.7377 20.7377 21.7377 22.7377 23.7377 24.7377 25.7377 26.7377 27.7377 28.7377 29.7377 30.7377 31.7377 32.7377 33.7377 34.7377 35.7377 36.7377 37.7377
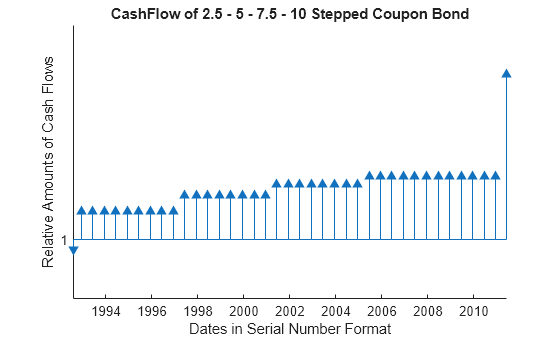
Visualize the third bond's cash flows (2.5 - 5 - 7.5 - 10) using the cfplot function.
cfplot(CDates(3,:),CFlows(3,:)); xlabel('Dates in Serial Number Format') ylabel('Relative Amounts of Cash Flows') title('CashFlow of 2.5 - 5 - 7.5 - 10 Stepped Coupon Bond')
Input Arguments
Settlement date, specified either as a scalar or
NSTP-by-1 vector using serial date numbers or
date character vectors.
Settle must be earlier than Maturity.
Data Types: double | char
Maturity date, specified as a scalar or an
NSTP-by-1 vector using serial date numbers or
date character vectors that represent the maturity date for each bond.
Data Types: double | char | string | datetime
Conversion dates, specified as a
NSTP-by-max(NCONV) matrix using serial date
numbers or date character vectors containing conversion dates after
Settle. The size of the matrix is equal to the number of
instruments by the maximum number of conversions. Fill unspecified entries with
NaN.
Data Types: double | char
Bond coupon rate, specified as an
NSTP-by-max(NCONV+1) matrix containing coupon
rates for each bond in the portfolio in decimal form. The matrix size is equal to the
number of instruments by maximum number of conversions + 1. First column of this matrix
contains rates applicable between Settle and the first conversion
date (date in the first column of ConvDates). Fill unspecified
entries with NaN
ConvDates has the same number of rows as
CouponRates to reflect the same number of bonds. However,
ConvDates has one less column than
CouponRates. This situation is illustrated by
Settle---------ConvDate1-----------ConvDate2------------Maturity
Rate1 Rate2 Rate3Data Types: double
(Optional) Coupons per year, specified as an
NSTP-by-1 vector. Values for
Period are 1, 2,
3, 4, 6, and
12.
Data Types: double
(Optional) Day-count basis of each instrument, specified as an
NSTP-by-1 vector.
0 = actual/actual
1 = 30/360 (SIA)
2 = actual/360
3 = actual/365
4 = 30/360 (PSA)
5 = 30/360 (ISDA)
6 = 30/360 (European)
7 = actual/365 (Japanese)
8 = actual/actual (ICMA)
9 = actual/360 (ICMA)
10 = actual/365 (ICMA)
11 = 30/360E (ICMA)
12 = actual/365 (ISDA)
13 = BUS/252
For more information, see Basis.
Data Types: double
(Optional) End-of-month rule flag for generating dates when
Maturity is an end-of-month date for a month having 30 or fewer
days, specified for each bond as a nonnegative integer [0,
1] using a NSTP-by-1 vector.
0= Ignore rule, meaning that a payment date is always the same numerical day of the month.1= Set rule on, meaning that a payment date is always the last actual day of the month.
Data Types: logical
(Optional) Face value, specified for each bond as an
NSTP-by-1 vector of nonnegative face
values.
Data Types: double
Output Arguments
Cash flow amounts, returned as a vector where the first entry in each row vector is the (negative) accrued interest due at settlement. If no accrued interest is due, the first column is zero.
Cash flow dates, returned as vector in serial date number form. At least two columns are always present: one for settlement and one for maturity.
Time factor for the SIA semiannual price/yield conversion, returned as a vector. The
SIA semi-annual price/yield conversion is DiscountFactor = (1 +
Yield/2).^(-TFactor). Time factors are in units of semiannual coupon
periods. For ISMA conventions: DiscountFactor = (1 +
Yield).^(-TFactor). Time factors are in units of annual coupon periods. In
computing time factors, use SIA actual/actual conventions for all time factor calculations.
Note
For bonds with fixed coupons, use cfamounts. If you use a fixed-coupon bond with
stepcpncfamounts, MATLAB® software generates an error.
More About
A stepped coupon is a type of bond or fixed-income security that features a coupon rate that increases (or "steps up") at predetermined intervals over the life of the bond.
The stepped coupon structure is designed to provide investors with higher interest payments as time progresses, making it attractive in environments where interest rates are expected to rise.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)