Arithmétique à virgule fixe

Addition et soustraction

L’addition de nombres à virgule fixe nécessite que les points binaires des opérandes soient alignés. On effectue ensuite l’addition en utilisant l’arithmétique binaire de façon à ce qu'aucun nombre autre que 0 ou 1 ne soit utilisé.

Par exemple, soit l’addition de 010010,1 (18,5) avec 0110,110 (6,75) :

$\begin{matrix} \begin{array}{r} \underline{\begin{matrix} 010010.1 \\ + 0110.110 \end{matrix}} \\ 011001.010 \end{array} & \begin{array}{l} (18.5) \\ (6.75) \\ (25.25) \end{array} \end{matrix}$

La soustraction à virgule fixe s’effectue de manière équivalente à l’addition en utilisant la valeur du complément à deux pour les valeurs négatives. Pour effectuer la soustraction, il faut procéder à une extension de signe des opérandes pour qu’ils aient la même longueur. Si, par exemple, vous devez soustraire 0110,110 (6,75) de 010010,1 (18,5) :

$\begin{matrix} \underline{\begin{matrix} 010010.100 \\ - 0110.110 \end{matrix}} & \begin{matrix} (18.5) \\ (6.75) \end{matrix} \end{matrix}$

La fimath globale par défaut a une valeur de 1 (vrai) pour la propriété CastBeforeSum. Ceci permet de convertir par cast les opérandes dans le type de données de la somme avant l'opération d’addition. Ainsi, il est inutile d’effectuer un autre changement lors de l’addition pour aligner les points binaires.

Si CastBeforeSum a une valeur de 0 (faux), les opérandes sont ajoutés en conservant toute la précision. La somme est quantifiée après l’addition.

Multiplication

La multiplication de nombres à virgule fixe en complément à deux est directement analogue à la multiplication décimale classique, avec la différence notable que les résultats intermédiaires doivent subir une extension de signe afin que leurs côtés gauches s’alignent avant que vous ne les ajoutiez.

Par exemple, soit la multiplication de 10,11 (-1,25) par 011 (3) :

Types de données utilisés pour la multiplication

Les diagrammes suivants montrent les types de données utilisés pour la multiplication à virgule fixe avec Fixed-Point Designer™. Ces diagrammes illustrent les différences entre les types de données utilisés pour la multiplication réel-réel, complexe-réel, et complexe-complexe.

Multiplication réel-réel. Les diagrammes suivants montrent les types de données utilisés par la toolbox pour la multiplication de deux nombres réels. Le software donne le résultat de cette opération dans le type de données du produit, qui est régi par la propriété ProductMode de l’objet fimath.

Multiplication réel-complexe. Le diagramme suivant montre les types de données utilisés par la toolbox pour la multiplication d‘un nombre réel et d’un nombre complexe à virgule fixe. Les multiplications réel-complexe et complexe-réel sont équivalentes. Le software donne le résultat de cette opération dans le type de données du produit, qui est régi par la propriété ProductMode de l’objet fimath :

Multiplication complexe-complexe. Le diagramme suivant montre la multiplication de deux nombres complexes à virgule fixe. Le software donne le résultat de cette opération dans le type de données de la somme, qui est régi par la propriété SumMode de l’objet fimath. Le type de données du produit intermédiaire est déterminé par la propriété ProductMode de l’objet fimath.

Lorsque la propriété CastBeforeSum de l’objet fimath est true, les casts en type de données de somme sont présents après les multiplicateurs dans le diagramme précédent. En code C, ceci est équivalent à

acc=ac;
acc-=bd;

pour le soustracteur, et à

acc=ad;
acc+=bc;

pour l’additionneur, où acc est l’accumulateur. Lorsque la propriété CastBeforeSum est false, les casts ne sont pas présents, et les données restent dans le type de données produit avant les opérations de soustraction et d’addition.

Multiplication avec fimath

Soit, dans les exemples suivants :

F = fimath('ProductMode','FullPrecision',...
'SumMode','FullPrecision');
T1 = numerictype('WordLength',24,'FractionLength',20);
T2 = numerictype('WordLength',16,'FractionLength',10);

Réel*réel. La longueur du mot et la longueur de la partie fractionnaire du résultat z sont respectivement égales à la somme des longueurs de mot et des longueurs des parties fractionnaires des multiplicandes. Ceci est dû au réglage sur FullPrecision des propriétés SumMode et ProductMode de l’objet fimath :

P = fipref;
P.FimathDisplay = 'none';
x = fi(5,T1,F)

x = 

     5

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10,T2,F)

y = 

    10

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

    50

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Réel*Complexe. La longueur du mot et la longueur de la partie fractionnaire du résultat z sont respectivement égales à la somme des longueurs de mot et des longueurs des parties fractionnaires des multiplicandes. Ceci est dû au réglage sur FullPrecision des propriétés SumMode et ProductMode de l’objet fimath :

x = fi(5,T1,F)

x = 

     5

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10+2i,T2,F)

y = 

  10.0000 + 2.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

  50.0000 +10.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Complexe*Complexe. Comme la multiplication complexe-complexe comporte une addition en plus d’une multiplication, la longueur de mot du résultat en précision complète possède un bit de plus que la somme des longueurs de mot des multiplicandes :

x = fi(5+6i,T1,F)

x = 

   5.0000 + 6.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10+2i,T2,F)

y = 

  10.0000 + 2.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y

z = 

  38.0000 +70.0000i

          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 41
        FractionLength: 30

Arithmétique modulaire

Les maths binaires sont basées sur l’arithmétique modulaire. L’arithmétique modulaire utilise uniquement un ensemble fini de nombres, réintégrant à l’intérieur de l’ensemble les résultats des calculs qui tombent en dehors de cet ensemble.

Par exemple, l’horloge que nous utilisons couramment tous les jours utilise l’arithmétique modulo 12. Dans ce système, les nombres ne peuvent être que les nombres de 1 à 12. C’est pourquoi, dans ce système d’« horloge », 9 plus 9 égale 6. Un cercle de nombres permet de visualiser cela plus facilement :

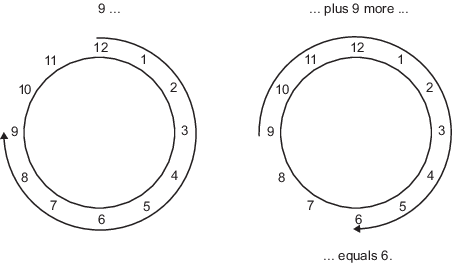
De la même manière, les maths binaires ne peuvent utiliser que les nombres 0 et 1, et tous les résultats arithmétiques qui tombent en dehors de cette plage sont réintégrés au « cercle » sous forme de 0 ou de 1.

Complément à deux

Le complément à deux est une manière d’interpréter un nombre binaire. Dans le complément à deux, les nombres positifs commencent toujours par un 0 et les nombres négatifs par un 1. Si le bit de gauche d’un nombre en complément à deux est 0, la valeur est obtenue en calculant la valeur binaire standard du nombre. Si le bit de gauche d’un nombre en complément à deux est 1, la valeur est obtenue en supposant que le bit le plus à gauche est négatif, puis en calculant la valeur binaire standard du nombre. Par exemple,

$\begin{array}{l} 01 = (0 + 2^{0}) = 1 \\ 11 = ((- 2^{1}) + (2^{0})) = (- 2 + 1) = - 1 \end{array}$

Pour calculer le négatif d’un nombre binaire en utilisant le complément à deux,

Prenez le complément à un, ou « inversez les bits ».
Ajoutez un 2^(-FL) en utilisant les maths binaires, où FL est la longueur de la partie fractionnaire.
Ignorez les bits s’étendant au-delà de la longueur de mot originale.

Par exemple, supposons que vous vouliez prendre le négatif de 11010 (-6). Prenez d’abord le complément à un du nombre, ce qui revient à inverser les bits :

$11010 \to 00101$

Ensuite, ajoutez un 1, en convertissant tous les nombres en 0 ou 1 :

$\begin{array}{l} \underline{\begin{array}{r} 00101 \\ + 1 \end{array}} \\ \begin{matrix} 00110 & (6) \end{matrix} \end{array}$

Casts

L’objet fimath vous permet de préciser le type de données et l’échelle des sommes et produits intermédiaires avec les propriétés SumMode et ProductMode. Il est important de garder à l’esprit les ramifications de chaque cast lorsque vous établissez les propriétés SumMode et ProductMode. Selon le type de données que vous sélectionnez, un overflow et/ou un arrondi peuvent survenir. Les deux exemples suivants montrent des cas où overflow et arrondi peuvent survenir.

Remarque

Pour d’autres exemples de casting (conversion de type), voir Cast fi Objects.

Casting d’un type de données plus court vers un type de données plus long

Prenons le cast d’un nombre différent de zéro, représenté par un type de données à 4 bits avec deux bits pour la fraction, en un type de données à 8 bits avec sept bits pour la fraction :

Comme le montre le diagramme, les bits source sont décalés vers la gauche de manière à ce que la virgule binaire corresponde à la position de la virgule binaire de destination. Le bit de source le plus élevé « sort » du nombre, ce qui peut provoquer un overflow, et le résultat peut saturer ou avoir à être réintégrer (wrap). Les bits vides à l’extrémité basse du type de données de destination sont comblés par des 0 ou des 1 :

S’il n’y a pas d'overflow, les bits vides sont comblés par des 0.
S’il y a une réintégration (wrapping), les bits vides sont comblés par des 0.
S’il y a saturation,
- les bits vides d’un nombre positif sont comblés par des 1.
- les bits vides d’un nombre négatif sont comblés par des 0.

On constate que même avec le cast d’un type de données plus court vers un type de données plus long, un overflow peut survenir. Ceci peut se produire lorsque la longueur de la partie entière du type de données source (dans ce cas deux) est supérieure à la longueur de la partie entière du type de données de destination (dans ce cas un). De la même manière, l’arrondi peut être nécessaire même lors du cast d’un type de données plus court vers un type de données plus long, si le type de données de destination et la mise à l’échelle ont moins de bits pour la fraction que la source.

Casting d’un type de données plus long vers un type de données plus court

Prenons le cast d’un nombre différent de zéro, représenté par un type de données à 8 bits avec sept bits pour la fraction, en un type de données à 4 bits avec deux bits pour la fraction :

Comme le montre le diagramme, les bits source sont décalés vers la droite de manière à ce que la virgule binaire corresponde à la position de la virgule binaire de destination. Étant donné qu’il n’y a pas de valeur pour le bit de poids le plus fort issu de la source, il faut utiliser une extension de signe pour remplir la partie entière du type de données de destination. L’extension de signe est l'addition de bits qui ont la valeur du bit de poids le plus fort à l’extrémité supérieure d’un nombre en complément à deux ; l’extension de signe ne change pas la valeur du nombre binaire. Les cinq bits de l’extrémité basse de la source ne rentrent pas dans la longueur de la partie fractionnaire de la destination. Le résultat est arrondi, d’où une perte possible de précision.

Dans ce cas, même si le cast s’effectue d’un type de données plus long vers un type de données plus court, tous les bits de la partie entière sont conservés. Réciproquement, une précision complète peut être conservée même lors du cast en type de données plus court, tant que la longueur de la partie fractionnaire du type de données de destination est identique ou supérieure à la longueur de la partie fractionnaire du type de données source. Dans ce cas, cependant, des bits sont perdus à l'extrémité gauche du résultat, et un overflow peut se produire.

Le cas le plus défavorable se produit lorsque la longueur de la partie entière et la longueur de la partie fractionnaire du type de données de destination sont inférieures à celles du type de données source et de l’échelle. Dans ce cas, on peut avoir un overflow et une perte de précision.