Normalized Reciprocal HDL Optimized

Computes normalized reciprocal using CORDIC algorithm and generates optimized HDL code

• 

Libraries:
Fixed-Point Designer HDL Support / Math Operations

Description

The Normalized Reciprocal HDL Optimized block computes the normalized reciprocal of u, returned as y and e such that 0.5 < |y| ≤ 1 and 2^ey = 1/u.

• If u = 0 and u is a fixed-point or scaled-double data type, then y = 1 – eps(y) and e = 2^nextpow2(w) – w + f, where w is the word length of u and f is the fraction length of u.

• If u = 0 and u is a floating-point data type, then y = Inf and e = 1.

Examples

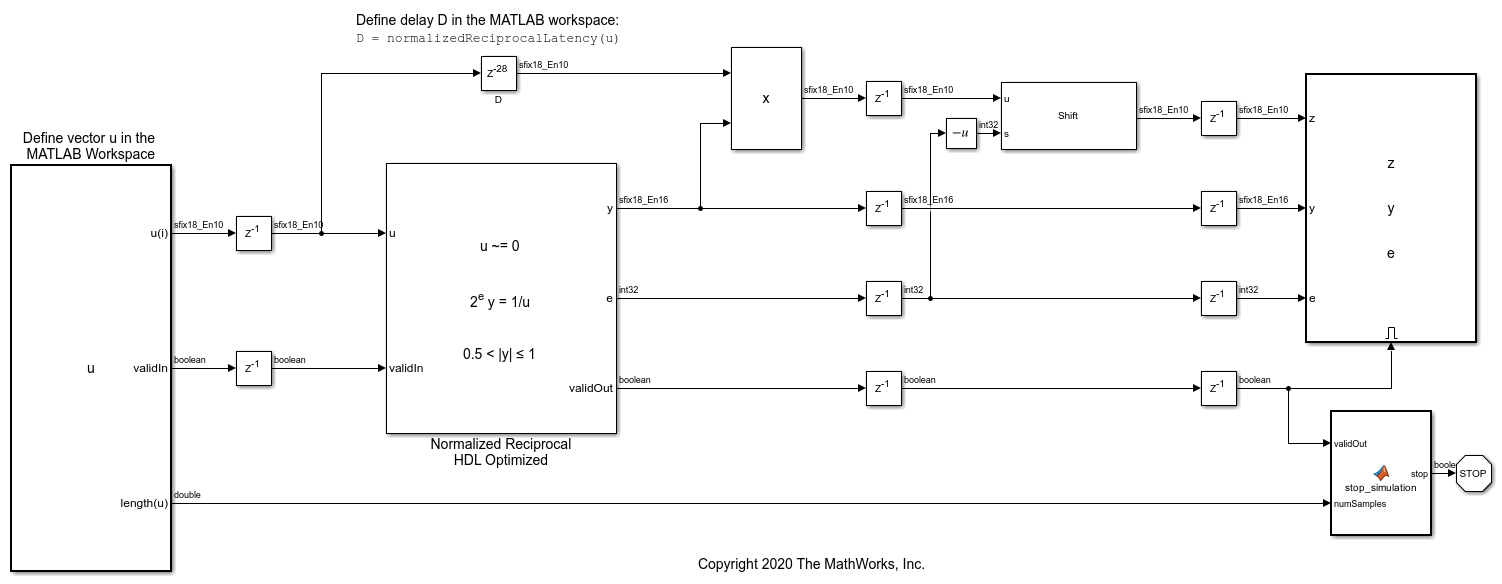
How to Use HDL Optimized Normalized Reciprocal

How and when to use the normalizedReciprocal function and the Normalized Reciprocal HDL Optimized block to compute the normalized reciprocal of an input.

• Open Script

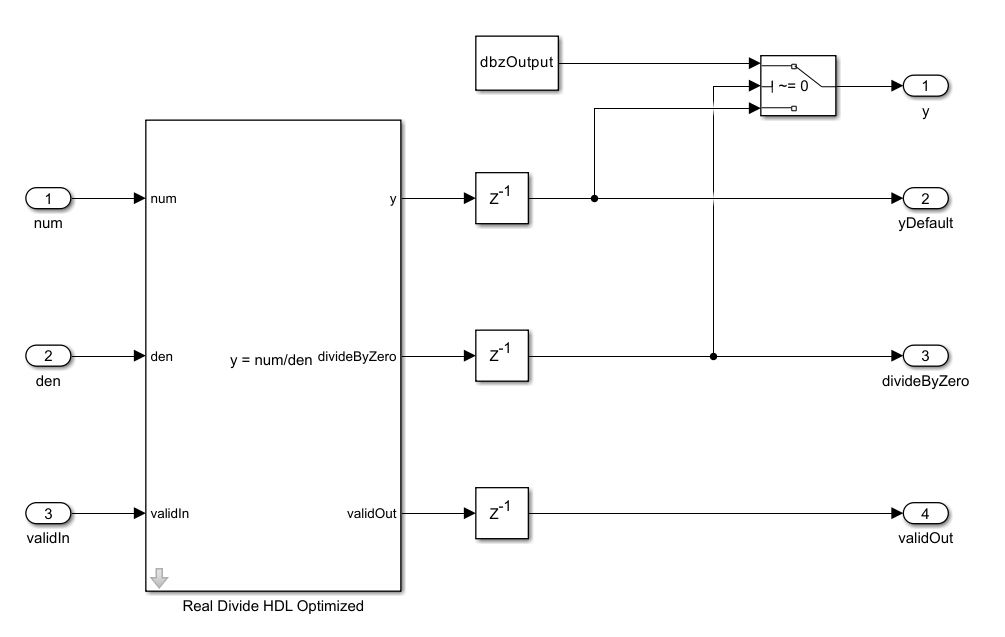
Customize Output Value of Real Divide HDL Optimized Block When Denominator Is Zero

Use the divideByZero port to customize the value of the block output when division by zero occurs.

• Open Live Script

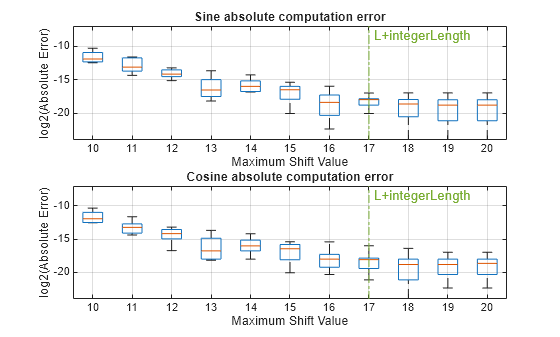
How to Set CORDIC Input Word Length and Maximum Shift Value to Achieve Desired Precision

Provides a starting point for the input data type and number of iterations or maximum shift value required for the CORDIC algorithm to achieve a desired accuracy.

• Open Live Script

Ports

Input

u — Value to take normalized reciprocal of

real scalar

Value to take the normalized reciprocal of, specified as a real scalar.

Slope-bias representation is not supported for fixed-point data types.

Data Types: single | double | fixed point

validIn — Whether input is valid

Boolean scalar

Whether input is valid, specified as a Boolean scalar. This control signal indicates when the data from the u input port is valid. When this value is 1 (true), the block captures the value at the u input port. When this value is 0 (false), the block ignores the input samples.

Data Types: Boolean

Output

y — Normalized reciprocal

scalar

Normalized reciprocal that satisfies 0.5 < |y| ≤ 1 and 2^ey = 1/u, returned as a scalar.

• If the input at port u is a signed fixed-point or scaled-double data type with word length w, then y is a signed fixed-point or scaled-double data type with word length w and fraction length w – 2.

• If the input at port u is an unsigned fixed-point or scaled-double data type with word length w, then y is an unsigned fixed-point or scaled-double data type with word length w and fraction length w – 1.

• If the input at port u is a double, then y is a double.

• If the input at port u is a single, the y is a single.

Data Types: single | double | fixed point

e — Exponent

integer scalar

Exponent that satisfies 0.5 < |y| ≤ 1 and 2^ey = 1/u, returned as an integer scalar.

Data Types: int32

divideByZero — Whether value at output is the result of division by zero

Boolean scalar

Since R2024b

Whether the values at the y and e output ports are the result of a division by zero operation, returned as a Boolean scalar. When the value of this signal is 1 (true), the corresponding output values at the y and e ports are the result of division by zero. When the value of this signal is 0 (false), the corresponding output values at the y and e ports are the result of division by a non-zero value.

Whether the divisor u is zero, returned as a Boolean scalar. When the value of this signal is 1 (true), the input at the u port is zero, resulting in a divide by zero operation. When the value of this signal is 0 (false), the input at the u port is a non-zero value.

Dependencies

• To enable this port, select the Show divide by zero port parameter.

Tips

• See Division by Zero Behavior for a description of the default divide by zero behavior.

Data Types: Boolean

validOut — Whether output data is valid

Boolean scalar

Whether the output data is valid, returned as a Boolean scalar. When the value of this control signal is 1 (true), the block has successfully computed the outputs at ports y and e. When this value is 0 (false), the output data is not valid.

Data Types: Boolean

Parameters

Show divide by zero port — Whether to show the divideByZero port

off (default) | on

Since R2024b

Select this parameter to show the divideByZero port.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	dbzPort
Values:	0 (false) (default) | 1 (true)
Data Types:	logical

Example: set_param(gcb,"dbzPort",1)

Automatically select CORDIC maximum shift value based on input word length — Automatically select CORDIC maximum shift value based on input word length

on (default) | off

Since R2024b

Automatically select CORDIC maximum shift value based on input word length. When this parameter is selected, the default CORDIC maximumShiftValue is equal to wl - 1, where wl = u.WordLength + ~issigned(u).

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	autoMaximumShiftVal
Values:	on (default) | off
Data Types:	char | string

Example: set_param(gcb,"autoMaximumShiftVal","off")

CORDIC maximum shift value — Maximum shift value of hyperbolic vectoring CORDIC

wl - 1 (default) | 10 | positive integer-valued scalar

Since R2024b

Maximum shift value of hyperbolic vectoring CORDIC, specified as a positive integer-valued scalar. The default value for this parameter is wl - 1, where wl = u.WordLength + ~issigned(u).

Dependencies

To enable this parameter, deselect the Automatically select CORDIC maximum shift value based on input word length parameter.

Tips

See Customizable Pipelining for more information.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	maximumShiftValue
Values:	10 (default) | positive integer-valued scalar
Data Types:	char | string

Example: set_param(gcb,"maximumShiftValue","10")

Number of iterations per pipeline register — Number of CORDIC iterations to perform per pipeline stage

1 (default) | positive integer-valued scalar

Since R2024b

Number of CORDIC iterations to perform per pipeline stage, specified as a positive integer-valued scalar.

Tips

• See Customizable Pipelining for more information.

• See How to Interface with the Normalized Reciprocal HDL Optimized Block and Hardware Resource Utilization for more information and examples showing how this parameter impacts latency and hardware resource utilization.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

To get the block parameter value programmatically, use the get_param function.

Parameter:	nIterPerReg
Values:	1 (default) | positive integer-valued scalar
Data Types:	char | string

Example: set_param(gcb,"nIterPerReg","2")

Tips

• The behavior of the Normalized Reciprocal HDL Optimized block is equivalent to the normalizedReciprocal function. When the data type of the input is fixed point with binary-point scaling, the function and block provide bit-exact results.

Algorithms

CORDIC

CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations (see References). The CORDIC algorithm eliminates the need for explicit multipliers. Using CORDIC, you can calculate various functions such as sine, cosine, arcsine, arccosine, arctangent, and vector magnitude. You can also use this algorithm for divide, square root, hyperbolic, and logarithmic functions.

The precision of the CORDIC algorithm is a function of the data type used and the maximum shift value or number of iterations of the CORDIC kernel. Using a data type with a larger word length and performing more iterations of the CORDIC algorithm can reduce the numeric error of the result. However, doing so also increases the latency of the computation and the utilizes more hardware resources. For more information, see How to Set CORDIC Input Word Length and Maximum Shift Value to Achieve Desired Precision.

How to Interface with the Normalized Reciprocal HDL Optimized Block

Because of its fully pipelined nature, the Normalized Reciprocal HDL Optimized block is able to accept input data on any cycle, including consecutive clock cycles. To send input data to the block, the validIn signal must be true. When the block has finished the computation and is ready to send the output, it will change validOut to true for one clock cycle. For inputs set of consecutive cycles, validOut will also be set to true on consecutive cycles.

The latency is defined from the input to the corresponding output. The latency depends on the input data type, as summarized in the table.

Input Type	Latency
Fixed point or scaled double fi	ceil((nextpow2(wl) + maximumShiftValue)/nIterPerReg) + 1 where wl = u.WordLength + ~issigned(u) and maximumShiftValue = wl - 1 or user-specified value.
Floating point	0

Customizable Pipelining

The Normalized Reciprocal HDL Optimized block uses fully-pipelined architecture that implements iterative normalization and a CORDIC-based division algorithm. If the input u is a fixed-point or scaled double data type, the block uses multiple pipeline stages for computation. If the input is a signed data type, the normalization requires nextpow2(u.WordLength) iterations. The number of CORDIC iterations depends on the value of the CORDIC maximum shift value parameter. A larger word length can provide higher resolution, but requires more iterations to process. The Normalized Reciprocal HDL Optimized block can perform multiple iterations per pipeline stage. This results in lower latency at the cost of a longer critical path in the generated HDL code.

For example, if the word length of the input u is 18, then normalization requires 5 iterations. If the Automatically select CORDIC maximum shift value based on input word length parameter is selected, the CORDIC maximum shift value is 18 - 1 = 17 and requires 17 iterations. The total number of iterations is 5 + 17 = 22 and the latency of the block is ceil((total number of iterations)/nIterPerReg) + 1. If the number of iterations per pipeline register is set to 1, then the block latency is 23; if the number of iterations per pipeline register is set to 2, then the block latency is 12; etc. If the number of iterations per pipeline register is greater than the total number of required iterations, the block performs all iterations in one pipeline stage and the total latency is minimized to 2.

Hardware Resource Utilization

This block supports HDL code generation using the Simulink^® HDL Workflow Advisor. For an example, see HDL Code Generation and FPGA Synthesis from Simulink Model (HDL Coder) and Implement Digital Downconverter for FPGA (DSP HDL Toolbox).

This example data was generated by synthesizing the block on a Xilinx^® Zynq^®-7000 xc7z045 SoC. The synthesis tool was Vivado^® v2023.1.2.

The following synthesis results show the effect of the Number of iterations per pipeline register parameter on the latency and hardware resource utilization.

nIterPerReg = 1

These parameters were used for synthesis:

• Input data type: sfix18_en10

• Automatically select CORDIC maximum shift value based on input word length: on

• Number of iterations per pipeline register: 1

• Target frequency: 500 MHz

• Latency for this configuration: 23

Resource	Usage	Available	Utilization (%)
Slice LUTs	586	218600	0.27
Slice Registers	703	437200	0.16
DSPs	0	900	0.00
Block RAM Tile	0	545	0.00
URAM	0	0

	Value
Requirement	2 ns (500 MHz)
Data Path Delay	1.74 ns
Slack	0.109 ns
Clock Frequency	528.82 MHz

nIterPerReg = 2

These parameters were used for synthesis:

• Input data type: sfix18_en10

• Automatically select CORDIC maximum shift value based on input word length: on

• Number of iterations per pipeline register: 2

• Target frequency: 300 MHz

• Latency for this configuration: 12

Resource	Usage	Available	Utilization (%)
Slice LUTs	470	218600	0.22
Slice Registers	374	437200	0.09
DSPs	0	900	0.00
Block RAM Tile	0	545	0.00
URAM	0	0

	Value
Requirement	3.3333 ns (300 MHz)
Data Path Delay	2.65 ns
Slack	0.676 ns
Clock Frequency	376.32 MHz

nIterPerReg = 3

These parameters were used for synthesis:

• Input data type: sfix18_en10

• Automatically select CORDIC maximum shift value based on input word length: on

• Number of iterations per pipeline register: 3

• Target frequency: 200 MHz

• Latency for this configuration: 9

Resource	Usage	Available	Utilization (%)
Slice LUTs	451	218600	0.21
Slice Registers	281	437200	0.06
DSPs	0	900	0.00
Block RAM Tile	0	545	0.00
URAM	0	0

	Value
Requirement	5 ns (200 MHz)
Data Path Delay	3.863 ns
Slack	1.13 ns
Clock Frequency	258.40 MHz

References

[1] Volder, Jack E. “The CORDIC Trigonometric Computing Technique.” IRE Transactions on Electronic Computers. EC-8, no. 3 (Sept. 1959): 330–334.

[2] Andraka, Ray. “A Survey of CORDIC Algorithm for FPGA Based Computers.” In Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays, 191–200. https://dl.acm.org/doi/10.1145/275107.275139.

[3] Walther, J.S. “A Unified Algorithm for Elementary Functions.” In Proceedings of the May 18-20, 1971 Spring Joint Computer Conference, 379–386. https://dl.acm.org/doi/10.1145/1478786.1478840.

[4] Schelin, Charles W. “Calculator Function Approximation.” The American Mathematical Monthly, no. 5 (May 1983): 317–325. https://doi.org/10.2307/2975781.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

Slope-bias representation is not supported for fixed-point data types.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

General
ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
In R2024b: FlattenHierarchy	Remove PWM Reference Generator block hierarchy from generated HDL code. The default is inherit. See also FlattenHierarchy (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Restrictions

Supports fixed-point data types only.

Version History

Introduced in R2020a

R2024b: Custom pipelining, improved latency and resource utilization, optional divide by zero port

Several improvements have been made to the Normalized Reciprocal HDL Optimized block:

• Custom pipelining is supported via the new CORDIC maximum shift value and Number of iterations per pipeline register parameters.

• The latency of this block has been reduced. Latency depends on the specified data type and pipeline configuration. See How to Interface with the Normalized Reciprocal HDL Optimized Block for more information.

• HDL resource utilization has been further optimized to require fewer hardware resources. See Hardware Resource Utilization for example synthesis results.

• An optional divideByZero port has been added to output a flag when the corresponding output is a result of division by zero.