NumericTypeScope
Determine fixed-point data type
Description
The NumericTypeScope object provides information about the
dynamic range of your data. The scope provides a visual representation of the dynamic range of
your data in the form of a log2 histogram.
Creation
Syntax
Description
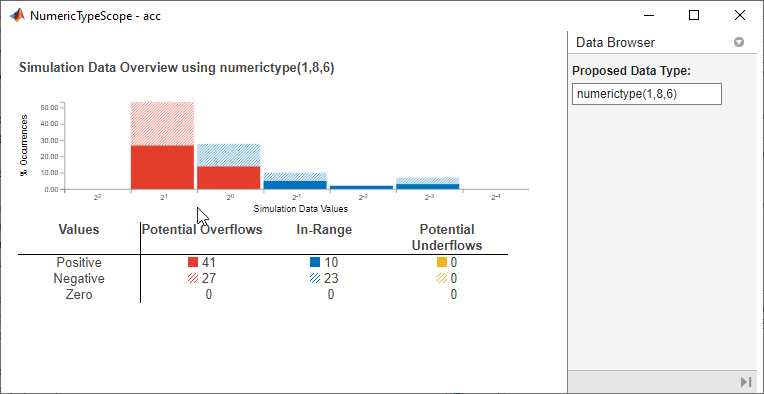
The NumericTypeScope window visualizes the dynamic range of a
fi object in a log2 histogram. Bit weights appear
along the x-axis of the histogram and the percentage of occurrences
along the y-axis. Each bin of the histogram corresponds to a bit in the
binary word. For example, 20 corresponds to the first integer bit in the binary word, and 2-1 corresponds to the first fractional bit in the binary word.
The NumericTypeScope identifies potential overflows and underflows
based on the current data type. The scope indicates values that may cause overflow or
underflow, or are in range of the data type by color-coding the histogram bars as
follows:
Blue — Histogram bin contains values that are in range of the current data type.
Red — Histogram bin contains values that may cause overflow.
Yellow — Histogram bin contains values that may cause underflow.
The table below the histogram breaks down each category of values by their signed value.
The Data Browser pane displays the current fixed-point data type as the Proposed Data Type. You can change the data type by entering a value directly in this box.