Minimisation contrainte à l'aide de l'algorithme génétique
Cet exemple montre comment minimiser une fonction objectif soumise à des contraintes et des limites d'inégalité non linéaire à l'aide de l'algorithme génétique.
Problème de minimisation sous contrainte
Pour ce problème, la fonction objectif à minimiser est une fonction simple d'une variable 2D x.
simple_objective(x) = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
Cette fonction est connue sous le nom de « cam », comme décrit dans L.C.W. Dixon et G.P. Szego [1].
De plus, le problème comporte des contraintes et des limites non linéaires.
x(1)*x(2) + x(1) - x(2) + 1.5 <= 0 (nonlinear constraint) 10 - x(1)*x(2) <= 0 (nonlinear constraint) 0 <= x(1) <= 1 (bound) 0 <= x(2) <= 13 (bound)
Coder la fonction fitness
Créez un fichier MATLAB nommé simple_objective.m contenant le code suivant :
type simple_objectivefunction y = simple_objective(x) %SIMPLE_OBJECTIVE Objective function for PATTERNSEARCH solver % Copyright 2004 The MathWorks, Inc. x1 = x(1); x2 = x(2); y = (4-2.1.*x1.^2+x1.^4./3).*x1.^2+x1.*x2+(-4+4.*x2.^2).*x2.^2;
Les solveurs tels que ga acceptent une seule entrée x, où x a autant d'éléments que le nombre de variables du problème. La fonction objectif calcule la valeur scalaire de la fonction objectif et la renvoie dans son argument de sortie unique y.
Coder la fonction de contrainte
Créez un fichier MATLAB nommé simple_constraint.m contenant le code suivant :
type simple_constraintfunction [c, ceq] = simple_constraint(x)
%SIMPLE_CONSTRAINT Nonlinear inequality constraints.
% Copyright 2005-2007 The MathWorks, Inc.
c = [1.5 + x(1)*x(2) + x(1) - x(2);
-x(1)*x(2) + 10];
% No nonlinear equality constraints:
ceq = [];
La fonction de contrainte calcule les valeurs de toutes les contraintes d'inégalité et d'égalité et renvoie respectivement les vecteurs c et ceq. La valeur de c représente les contraintes d’inégalité non linéaire que le solveur tente de rendre inférieures ou égales à zéro. La valeur de ceq représente les contraintes d’égalité non linéaires que le solveur tente de rendre égales à zéro. Cet exemple n'a pas de contraintes d'égalité non linéaire, donc ceq = []. Pour plus de détails, voir Nonlinear Constraints.
Minimiser en utilisant ga
Spécifiez la fonction objectif comme un handle de fonction.
ObjectiveFunction = @simple_objective;
Spécifiez les limites du problème.
lb = [0 0]; % Lower bounds ub = [1 13]; % Upper bounds
Spécifiez la fonction de contrainte non linéaire comme un handle de fonction.
ConstraintFunction = @simple_constraint;
Spécifiez le nombre de variables du problème.
nvars = 2;
Appelez le solveur en demandant le point optimal x et la valeur de la fonction au point optimal fval.
rng default % For reproducibility [x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub,ConstraintFunction)
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
x = 1×2
0.8122 12.3103
fval = 9.1268e+04
Ajouter une visualisation
Pour observer la progression du solveur, spécifiez des options qui sélectionnent deux fonctions de tracé. La fonction de tracé gaplotbestf trace la meilleure valeur de fonction objectif à chaque itération, et la fonction de tracé gaplotmaxconstr trace la violation de contrainte maximale à chaque itération. Définissez ces deux fonctions de tracé dans un cell array. Affichez également des informations sur la progression du solveur dans la fenêtre de commande en définissant l'option Display sur 'iter'.
options = optimoptions("ga",'PlotFcn',{@gaplotbestf,@gaplotmaxconstr}, ... 'Display','iter');
Exécutez le solveur, y compris l’argument options.
[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ...
ConstraintFunction,options)Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2524 91986.8 7.796e-09 0
2 4986 94678.2 0 0
3 10362 96473.7 0 0
4 16243 91270.1 0.0009897 0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
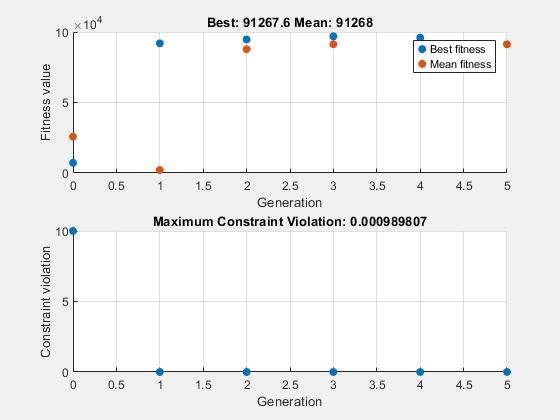
x = 1×2
0.8123 12.3104
fval = 9.1270e+04
Avec l'affichage itératif, ga fournit des détails sur le type de problème et les opérateurs de création, de croisement, de mutation et de sélection.
Les contraintes non linéaires obligent ga à résoudre de nombreux sous-problèmes à chaque itération. Comme le montrent les graphiques et l’affichage itératif, le processus de résolution comporte peu d’itérations. Cependant, la colonne Func-count dans l'affichage itératif montre de nombreuses évaluations de fonctions par itération.
Le solveur ga gère les contraintes et les limites linéaires différemment des contraintes non linéaires. Toutes les contraintes et limites linéaires sont satisfaites tout au long de l’optimisation. Cependant, ga peut ne pas satisfaire toutes les contraintes non linéaires à chaque génération. Si ga converge vers une solution, les contraintes non linéaires seront satisfaites à cette solution.
ga utilise les fonctions de mutation et de croisement pour produire de nouveaux individus à chaque génération. La manière dont ga satisfait les contraintes linéaires et bornées est d'utiliser des fonctions de mutation et de croisement qui ne génèrent que des points réalisables. Par exemple, dans l'appel précédent à ga, la fonction de mutation par défaut (pour les problèmes sans contraintes) mutationgaussian ne satisfait pas les contraintes linéaires et donc ga utilise la fonction mutationadaptfeasible par défaut. Si vous fournissez une fonction de mutation personnalisée, cette fonction personnalisée doit uniquement générer des points réalisables par rapport aux contraintes linéaires et bornées. Toutes les fonctions de croisement de la boîte à outils génèrent des points qui satisfont les contraintes et les limites linéaires.
Cependant, lorsque votre problème contient des contraintes entières, ga garantit que toutes les itérations satisfont aux limites et aux contraintes linéaires. Cette faisabilité se produit pour tous les opérateurs de mutation, de croisement et de création, à une faible tolérance près.
Fournir un point de départ
Pour accélérer le solveur, vous pouvez fournir une population initiale dans l'option InitialPopulationMatrix. ga utilise la population initiale pour démarrer son optimisation. Spécifiez un vecteur de ligne ou une matrice où chaque ligne représente un point de départ.
X0 = [0.8 12.5]; % Start point (row vector) options.InitialPopulationMatrix = X0; [x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ... ConstraintFunction,options)
Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2500 91769.6 0 0
2 4962 97536.4 0 0
3 7412 91268.4 0.00098 0
4 9862 91268.1 0.0009893 0
5 12312 91267.9 0.0009943 0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
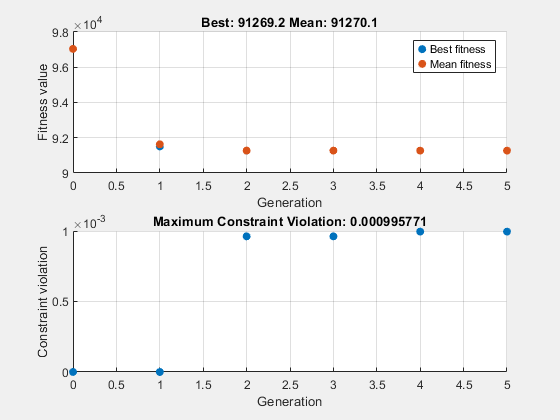
x = 1×2
0.8122 12.3103
fval = 9.1268e+04
Dans ce cas, fournir un point de départ ne modifie pas substantiellement la progression du solveur.
Références
[1] Dixon, L. C. W., et G .P. Szego (éd.). Towards Global Optimisation 2. North-Holland : Elsevier Science Ltd., Amsterdam, 1978.