Cette page a été traduite par traduction automatique. Cliquez ici pour voir la dernière version en anglais.

Optimisation globale et locale avec ga

À la recherche d'un minimum mondial

Parfois, l’objectif d’une optimisation est de trouver le minimum ou le maximum global d’une fonction, c’est-à-dire un point où la valeur de la fonction est plus petite ou plus grande à tout autre point de l’espace de recherche. Cependant, les algorithmes d’optimisation renvoient parfois un minimum local, c’est-à-dire un point où la valeur de la fonction est plus petite qu’aux points proches, mais éventuellement plus grande qu’à un point éloigné de l’espace de recherche. L'algorithme génétique peut parfois surmonter cette déficience avec les bons réglages.

À titre d’exemple, considérons la fonction suivante.

$$f(x)=\{\begin{array}{ll}-\exp \left(-{\left(\frac{x}{100}\right)}^2\right)& forx\le 100,\\ -\exp (-1)+(x-100)(x-102)& forx>100.\end{array}$$

Tracez la fonction.

t = -10:.1:103;
for ii = 1:length(t)
    y(ii) = two_min(t(ii));
end
plot(t,y)

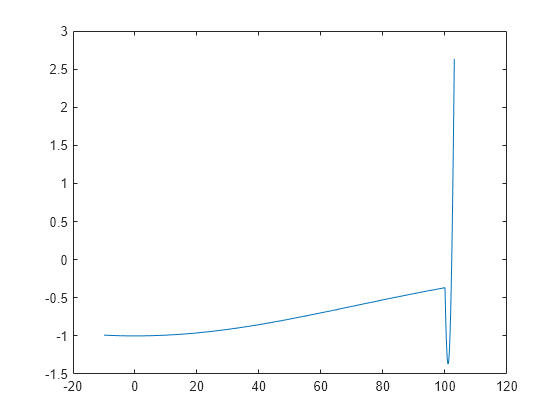
La fonction a deux minima locaux, l'un à $$x=0$$, où la valeur de la fonction est –1, et l'autre à $$x=101$$, où la valeur de la fonction est $$–1–1/e$$. Comme cette dernière valeur est plus petite, le minimum global se produit à $$x=101$$.

Exécutez ga en utilisant les paramètres par défaut

Le code de la fonction d'aide two_min se trouve à la fin de cet exemple. Exécutez ga avec les paramètres par défaut pour minimiser la fonction two_min. Utilisez la fonction d'aide gaplot1drange (incluse à la fin de cet exemple) pour tracer la plage de la population ga à chaque itération.

rng default % For reproducibility
options = optimoptions('ga','PlotFcn',@gaplot1drange);
[x,fval] = ga(@two_min,1,[],[],[],[],[],[],[],options)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

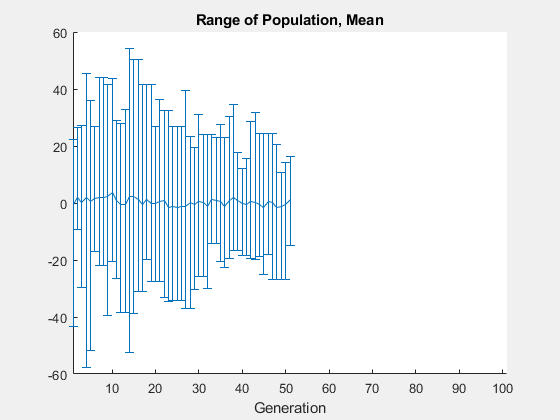
x = 
-0.0688

fval = 
-1.0000

L'algorithme génétique renvoie un point très proche du minimum local à $$x=0$$. Notez que tous les individus se situent entre –60 et 60. La population n'explore jamais les points proches du minimum global à $$x=101$$.

Augmenter la portée initiale

Une façon de permettre à l’algorithme génétique d’explorer une gamme plus large de points, c’est-à-dire d’augmenter la diversité des populations, est d’augmenter la gamme initiale. La plage initiale ne doit pas nécessairement inclure le point x = 101, mais elle doit être suffisamment grande pour que l’algorithme génère des individus proches de x = 101. Définissez l’option InitialPopulationRange sur [-10;90] et réexécutez le solveur.

options.InitialPopulationRange = [-10;90];
[x,fval] = ga(@two_min,1,[],[],[],[],[],[],[],options)

ga stopped because it exceeded options.MaxGenerations.

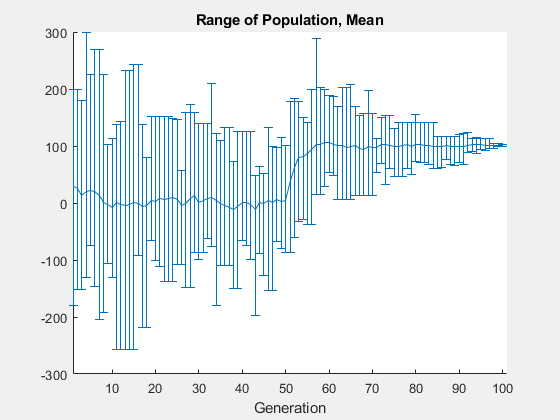
x = 
100.9783

fval = 
-1.3674

Cette fois, le graphique personnalisé montre un éventail beaucoup plus large d’individus. Il y a des individus proches de 101 dès le début, et la moyenne de la population commence à converger vers 101.

Fonctions d'assistance

Ce code crée la fonction d'assistance two_min.

function y = two_min(x)
if x <= 100
    y = -exp(-(x/100)^2);
else
    y = -exp(-1) + (x-100)*(x-102);
end
end

Ce code crée la fonction d'assistance gaplot1drange.

function state = gaplot1drange(options,state,flag)
%gaplot1drange Plots the mean and the range of the population.
%   STATE = gaplot1drange(OPTIONS,STATE,FLAG) plots the mean and the range
%   (highest and the lowest) of individuals (1-D only).  
%
%   Example:
%   Create options that use gaplot1drange
%   as the plot function
%     options = optimoptions('ga','PlotFcn',@gaplot1drange);

%   Copyright 2012-2014 The MathWorks, Inc.

if isinf(options.MaxGenerations) || size(state.Population,2) > 1
    title('Plot Not Available','interp','none');
    return;
end
generation = state.Generation;
score = state.Population;
smean = mean(score);
Y = smean;
L = smean - min(score);
U = max(score) - smean;

switch flag

    case 'init'
        set(gca,'xlim',[1,options.MaxGenerations+1]);
        plotRange = errorbar(generation,Y,L,U);
        set(plotRange,'Tag','gaplot1drange');
        title('Range of Population, Mean','interp','none')
        xlabel('Generation','interp','none')
    case 'iter'
        plotRange = findobj(get(gca,'Children'),'Tag','gaplot1drange');
        newX = [get(plotRange,'Xdata') generation];
        newY = [get(plotRange,'Ydata') Y];
        newL = [get(plotRange,'Ldata') L];
        newU = [get(plotRange,'Udata') U];       
        set(plotRange,'Xdata',newX,'Ydata',newY,'Ldata',newL,'Udata',newU);
end
end

Voir aussi

Rubriques

• What Is Global Optimization?
• Population Diversity
• Isolated Global Minimum