Cette page a été traduite par traduction automatique. Cliquez ici pour voir la dernière version en anglais.

Codage et minimisation d'une fonction fitness à l'aide de l'algorithme génétique

Ouvrir le live script

Cet exemple montre comment créer et minimiser une fonction fitness pour le solveur d'algorithme génétique ga en utilisant trois techniques :

  • Basique

  • Inclure des paramètres supplémentaires

  • Vectorisé pour plus de vitesse

Fonction fitness de base

La fonction fitness de base est la fonction de Rosenbrock, une fonction de test courante pour les optimiseurs. La fonction est une somme de carrés :

f(x)=100(x12-x2)2+(1-x1)2.

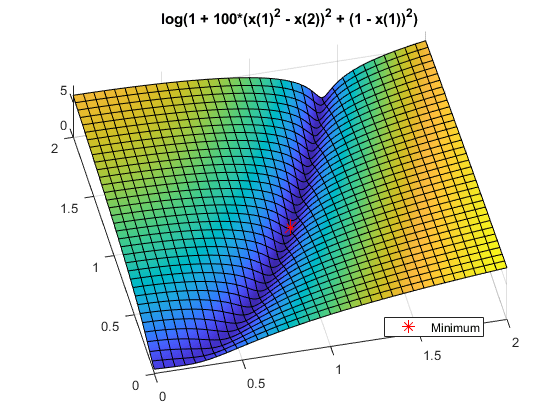
La fonction a une valeur minimale de zéro au point [1,1]. Étant donné que la fonction de Rosenbrock est assez raide, tracez le logarithme de un plus la fonction.

fsurf(@(x,y)log(1 + 100*(x.^2 - y).^2 + (1 - x).^2),[0,2])
title('log(1 + 100*(x(1)^2 - x(2))^2 + (1 - x(1))^2)')
view(-13,78)
hold on
h1 = plot3(1,1,0.1,'r*','MarkerSize',12);
legend(h1,'Minimum','Location','best');
hold off

Code d'une fonction fitness

Le fichier de fonction simple_fitness implémente la fonction de Rosenbrock.

type simple_fitness
function y = simple_fitness(x)
%SIMPLE_FITNESS fitness function for GA

%   Copyright 2004 The MathWorks, Inc. 

  y = 100 * (x(1)^2 - x(2)) ^2 + (1 - x(1))^2;

Une fonction fitness doit prendre une entrée x où x est un vecteur de lignes avec autant d'éléments que de variables dans le problème. La fonction fitness calcule la valeur de la fonction et renvoie cette valeur scalaire dans son seul argument de retour y.

Réduire à l'aide de ga

Pour minimiser la fonction fitness à l'aide de ga, transmettez un handle de fonction à la fonction fitness ainsi que le nombre de variables dans le problème. Pour que ga examine la région concernée, incluez les limites -3 <= x(i) <= 3. Transmettez les limites comme cinquième et sixième arguments après numberOfVariables. Pour les détails de la syntaxe ga, voir ga.

ga est un algorithme aléatoire. Pour la reproductibilité, définissez le flux de nombres aléatoires.

rng default % For reproducibility
FitnessFunction = @simple_fitness;
numberOfVariables = 2;
lb = [-3,-3];
ub = [3,3];
[x,fval] = ga(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub)
Optimization terminated: maximum number of generations exceeded.

x = 1×2

    1.5083    2.2781


fval = 0.2594

Le x renvoyé par le solveur est le meilleur point de la population finale calculé par ga. fval est la valeur de la fonction simple_fitness évaluée au point x. ga n'a pas trouvé de solution particulièrement bonne. Pour connaître les moyens d’améliorer la solution, voir Effets des options d'algorithmes génétiques.

Fonction Fitness avec paramètres supplémentaires

Parfois, votre fonction fitness comporte des paramètres supplémentaires qui agissent comme des constantes pendant l'optimisation. Par exemple, une fonction de Rosenbrock généralisée peut avoir des paramètres supplémentaires représentant les constantes 100 et 1 :

f(x,a,b)=a(x12-x2)2+(b-x1)2.

a et b sont des paramètres de la fonction fitness qui agissent comme des constantes pendant l'optimisation (ils ne sont pas modifiés dans le cadre de la minimisation). Le fichier parameterized_fitness.m implémente cette fonction fitness paramétrée.

type parameterized_fitness
function y = parameterized_fitness(x,p1,p2)
%PARAMETERIZED_FITNESS fitness function for GA

%   Copyright 2004 The MathWorks, Inc.        
 
y = p1 * (x(1)^2 - x(2)) ^2 + (p2 - x(1))^2;

Minimiser une fonction en utilisant des paramètres supplémentaires

Utilisez une fonction anonyme pour capturer les valeurs des arguments supplémentaires, à savoir les constantes a et b. Créez un handle de fonction FitnessFunction vers une fonction anonyme qui prend une entrée x et appelle parameterized_fitness avec x, a et b. La fonction anonyme contient les valeurs de a et b qui existent lorsque le handle de fonction est créé.

a = 100;
b = 1; % define constant values
FitnessFunction = @(x) parameterized_fitness(x,a,b);
[x,fval] = ga(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub)
Optimization terminated: maximum number of generations exceeded.

x = 1×2

    1.3198    1.7434


fval = 0.1025

Voir Passing Extra Parameters.

Fonction fitness vectorisée

Pour gagner en vitesse, vectorisez votre fonction fitness. Une fonction fitness vectorisée calcule la fitness d'un ensemble de points à la fois, ce qui permet généralement de gagner du temps par rapport à l'évaluation individuelle de ces points. Pour écrire une fonction fitness vectorisée, faites en sorte que votre fonction accepte une matrice, où chaque ligne de matrice représente un point, et faites en sorte que la fonction fitness renvoie un vecteur colonne de valeurs de fonction fitness.

Pour modifier le fichier de fonction parameterized_fitness en une forme vectorisée :

  • Changez chaque variable x(i) en x(:,i), c'est-à-dire le vecteur colonne de variables correspondant à x(i).

  • Remplacez chaque multiplication vectorielle * par .* et chaque exponentiation ^ par .^, indiquant que les opérations sont élément par élément. Il n'y a pas de multiplications vectorielles dans ce code, il suffit donc de changer les exposants.

type vectorized_fitness
function y = vectorized_fitness(x,p1,p2)
%VECTORIZED_FITNESS fitness function for GA

%   Copyright 2004-2010 The MathWorks, Inc.  

y = p1 * (x(:,1).^2 - x(:,2)).^2 + (p2 - x(:,1)).^2;

Cette version vectorisée de la fonction fitness prend une matrice x avec un nombre arbitraire de points, c'est-à-dire un nombre arbitraire de lignes, et renvoie un vecteur colonne y avec le même nombre de lignes que x.

Indiquez au solveur que la fonction fitness est vectorisée dans l'option 'UseVectorized'.

options = optimoptions(@ga,'UseVectorized',true);

Inclure les options comme dernier argument de ga.

VFitnessFunction = @(x) vectorized_fitness(x,100,1);
[x,fval] = ga(VFitnessFunction,numberOfVariables,[],[],[],[],lb,ub,[],options)
Optimization terminated: maximum number of generations exceeded.

x = 1×2

    1.6219    2.6334


fval = 0.3876

Quelle est la différence de vitesse ? Chronométrez l'optimisation avec et sans vectorisation.

tic
[x,fval] = ga(VFitnessFunction,numberOfVariables,[],[],[],[],lb,ub,[],options);
Optimization terminated: maximum number of generations exceeded.

v = toc;
tic
[x,fval] = ga(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub);
Optimization terminated: maximum number of generations exceeded.

nv = toc;
fprintf('Using vectorization took %f seconds. No vectorization took %f seconds.\n',v,nv)
Using vectorization took 0.153337 seconds. No vectorization took 0.212880 seconds.

Dans ce cas, l’amélioration par vectorisation n’a pas été grande, car le calcul de la fonction fitness prend très peu de temps. Cependant, pour les fonctions fitness plus chronophages, la vectorisation peut être utile. Voir Vectorize the Fitness Function.

Voir aussi

Rubriques