Cette page a été traduite par traduction automatique. Cliquez ici pour voir la dernière version en anglais.

ga

Trouver le minimum de fonction en utilisant un algorithme génétique

Syntaxe

x = ga(fun,nvars)

x = ga(fun,nvars,A,b)

x = ga(fun,nvars,A,b,Aeq,beq)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

x = ga(problem)

[x,fval] = ga(___)

[x,fval,exitflag,output] = ga(___)

[x,fval,exitflag,output,population,scores] = ga(___)

Description

x = ga(fun,nvars) trouve un minimum local non contraint, x, pour la fonction objectif, fun. nvars est la dimension (nombre de variables de conception) de fun.

Remarque

Passing Extra Parameters explique comment passer des paramètres supplémentaires à la fonction objectif et aux fonctions de contrainte non linéaire, si nécessaire.

x = ga(fun,nvars,A,b) trouve un minimum local x à fun, soumis aux inégalités linéaires A*x ≤ b. ga évalue le produit matriciel A*x comme si x était transposé (A*x').

x = ga(fun,nvars,A,b,Aeq,beq) trouve un minimum local x à fun, sous réserve des égalités linéaires Aeq*x = beq et A*x ≤ b. (Définissez A=[] et b=[] si aucune inégalité linéaire n'existe.) ga évalue le produit matriciel Aeq*x comme si x était transposé (Aeq*x').

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub) définit un ensemble de limites inférieures et supérieures sur les variables de conception, x, de sorte qu'une solution soit trouvée dans la plage lb ≤ x ≤ ub. (Définissez Aeq=[] et beq=[] si aucune égalité linéaire n’existe.)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon) soumet la minimisation aux contraintes définies dans nonlcon. La fonction nonlcon accepte x et renvoie les vecteurs C et Ceq, représentant respectivement les inégalités et égalités non linéaires. ga minimise les fun tels que C(x) ≤ 0 et Ceq(x) = 0. (Définissez lb=[] et ub=[] si aucune limite n'existe.)

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,options) minimise avec les paramètres d'optimisation par défaut remplacés par des valeurs dans options. (Définissez nonlcon=[] si aucune contrainte non linéaire n’existe.) Créez options en utilisant optimoptions.

x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon) ou x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options) nécessite que les variables répertoriées dans intcon prennent des valeurs entières.

Remarque

Lorsqu'il y a des contraintes d'entier, ga n'accepte pas les contraintes d'égalité non linéaires, uniquement les contraintes d'inégalité non linéaires.

x = ga(problem) trouve le minimum pour problem, une structure décrite dans problem.

[x,fval] = ga(___), pour tous les arguments en entrée précédents, renvoie également fval, la valeur de la fonction fitness à x.

[x,fval,exitflag,output] = ga(___) renvoie également exitflag, un entier identifiant la raison pour laquelle l'algorithme s'est terminé, et output, une structure qui contient la sortie de chaque génération et d'autres informations sur les performances de l'algorithme.

[x,fval,exitflag,output,population,scores] = ga(___) renvoie également une matrice population, dont les lignes sont la population finale, et un vecteur scores, les scores de la population finale.

Exemples

Optimiser une fonction non lisse à l'aide de ga

Le fichier ps_example.m est inclus lorsque vous exécutez cet exemple. Tracez la fonction.

xi = linspace(-6,2,300);
yi = linspace(-4,4,300);
[X,Y] = meshgrid(xi,yi);
Z = ps_example([X(:),Y(:)]);
Z = reshape(Z,size(X));
surf(X,Y,Z,'MeshStyle','none')
colormap 'jet'
view(-26,43)
xlabel('x(1)')
ylabel('x(2)')
title('ps\_example(x)')

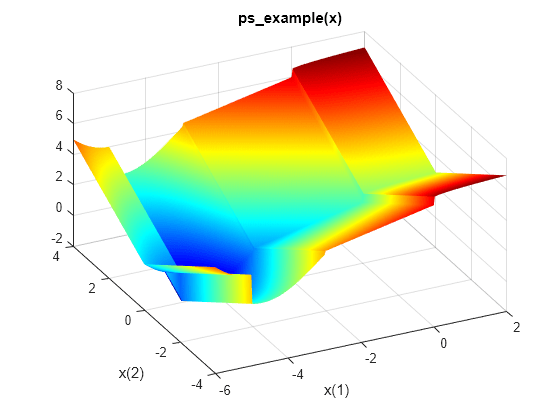
Trouvez le minimum de cette fonction en utilisant ga.

rng default % For reproducibility
x = ga(@ps_example,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6793   -0.0860

Minimiser une fonction non lisse avec des contraintes linéaires

Utilisez l'algorithme génétique pour minimiser la fonction ps_example sur la région x(1) + x(2) >= 1 et x(2) <= 5 + x(1). Cette fonction est incluse lorsque vous exécutez cet exemple.

Tout d’abord, convertissez les deux contraintes d’inégalité sous la forme matricielle A*x <= b. En d'autres termes, récupérez les variables x du côté gauche de l'inégalité et rendez les deux inégalités inférieures ou égales :

-x(1) -x(2) <= -1

-x(1) + x(2) <= 5

A = [-1,-1;
    -1,1];
b = [-1;5];

Résolvez le problème contraint en utilisant ga.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    0.9990    0.0000

Les contraintes sont satisfaites dans la limite de la valeur par défaut de la tolérance de contrainte, 1e-3. Pour voir cela, calculez A*x' - b, qui devrait avoir des composantes négatives.

disp(A*x' - b)

    0.0010
   -5.9990

Minimiser une fonction non lisse avec des contraintes d'égalité et d'inégalité linéaires

Utilisez l'algorithme génétique pour minimiser la fonction ps_example sur la région x(1) + x(2) >= 1 et x(2) == 5 + x(1). Cette fonction est incluse lorsque vous exécutez cet exemple.

Tout d’abord, convertissez les deux contraintes sous la forme matricielle A*x <= b et Aeq*x = beq. En d'autres termes, récupérez les variables x du côté gauche des expressions et transformez l'inégalité en forme inférieure ou égale :

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Résolvez le problème contraint en utilisant ga.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -2.0005    2.9995

Vérifiez que les contraintes sont satisfaites dans la limite de la valeur par défaut de ConstraintTolerance, 1e-3.

disp(A*x' - b)

   1.0000e-03

disp(Aeq*x' - beq)

   8.5897e-09

Optimiser avec des contraintes et des limites linéaires

Utilisez l'algorithme génétique pour minimiser la fonction ps_example sur la région x(1) + x(2) >= 1 et x(2) == 5 + x(1). La fonction ps_example est incluse lorsque vous exécutez cet exemple. De plus, définissez les limites 1 <= x(1) <= 6 et -3 <= x(2) <= 8.

Tout d’abord, convertissez les deux contraintes linéaires sous la forme matricielle A*x <= b et Aeq*x = beq. En d'autres termes, récupérez les variables x du côté gauche des expressions et transformez l'inégalité en forme inférieure ou égale :

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Définissez les limites lb et ub.

lb = [1 -3];
ub = [6 8];

Résolvez le problème contraint en utilisant ga.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,lb,ub)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

    1.0000    6.0000

Vérifiez que les contraintes linéaires sont satisfaites dans la limite de la valeur par défaut de ConstraintTolerance, 1e-3.

disp(A*x' - b)

   -6.0000

disp(Aeq*x' - beq)

  -7.9765e-08

Optimiser avec des contraintes non linéaires à l'aide de ga

Utilisez l'algorithme génétique pour minimiser la fonction ps_example sur la région $2{\mathit{x}}_1^2+{\mathit{x}}_2^2\le 3$ et $$(x_1+1{)}^2=(x_2/2{)}^4$$. La fonction ps_example est incluse lorsque vous exécutez cet exemple.

Pour ce faire, utilisez la fonction ellipsecons.m qui renvoie la contrainte d’inégalité dans la première sortie, c, et la contrainte d’égalité dans la deuxième sortie, ceq. La fonction ellipsecons est incluse lorsque vous exécutez cet exemple. Examinez le code ellipsecons.

type ellipsecons

function [c,ceq] = ellipsecons(x)

c = 2*x(1)^2 + x(2)^2 - 3;
ceq = (x(1)+1)^2 - (x(2)/2)^4;

Inclure un handle de fonction pour ellipsecons comme argument nonlcon.

nonlcon = @ellipsecons;
fun = @ps_example;
rng default % For reproducibility
x = ga(fun,2,[],[],[],[],[],[],nonlcon)

Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -0.9766    0.0362

Vérifiez que les contraintes non linéaires sont satisfaites à x. Les contraintes sont satisfaites lorsque c ≤ 0 et ceq = 0 dans la valeur par défaut de ConstraintTolerance, 1e-3.

[c,ceq] = nonlcon(x)

c = 
-1.0911

ceq = 
5.4645e-04

Minimiser une fonction avec des options n'utilisant pas les valeurs par défaut

Utilisez l'algorithme génétique pour minimiser la fonction ps_example sur la région x(1) + x(2) >= 1 et x(2) == 5 + x(1) en utilisant une tolérance de contrainte inférieure à la valeur par défaut. La fonction ps_example est incluse lorsque vous exécutez cet exemple.

Tout d’abord, convertissez les deux contraintes sous la forme matricielle A*x <= b et Aeq*x = beq. En d'autres termes, récupérez les variables x du côté gauche des expressions et transformez l'inégalité en forme inférieure ou égale :

-x(1) -x(2) <= -1

-x(1) + x(2) == 5

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;

Pour obtenir une solution plus précise, définissez une tolérance de contrainte de 1e-6. Et pour surveiller la progression du solveur, définissez une fonction de tracé.

options = optimoptions('ga','ConstraintTolerance',1e-6,'PlotFcn', @gaplotbestf);

Résolvez le problème de minimisation.

rng default % For reproducibility
fun = @ps_example;
x = ga(fun,2,A,b,Aeq,beq,[],[],[],options)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

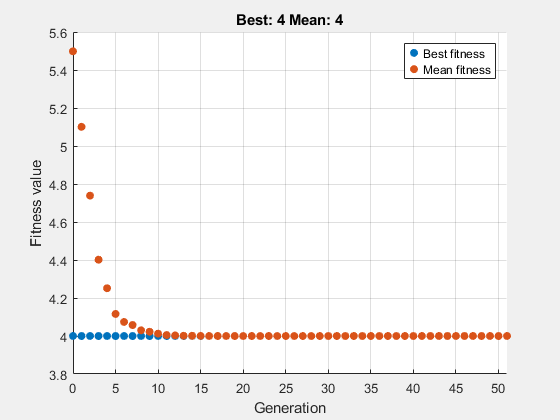
x = 1×2

   -2.0000    3.0000

Vérifiez que les contraintes linéaires sont satisfaites à 1e-6 près.

disp(A*x' - b)

   9.9809e-07

disp(Aeq*x' - beq)

  -7.3589e-08

Minimiser une fonction non linéaire avec des contraintes entières

Utilisez l'algorithme génétique pour minimiser la fonction ps_example sous la contrainte que x(1) est un entier. Cette fonction est incluse lorsque vous exécutez cet exemple.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
x = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

Obtenir la solution et la valeur de la fonction

Utiliser l’algorithme génétique pour minimiser un problème non linéaire contraint par des nombres entiers. Obtenez à la fois l’emplacement du minimum et la valeur minimale de la fonction. La fonction objectif, ps_example, est incluse lorsque vous exécutez cet exemple.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon)

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = 
-1.8344

Comparez ce résultat à la solution du problème sans contraintes.

[x,fval] = ga(fun,2)

ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2

   -4.6906   -0.0078

fval = 
-1.9918

Obtenir des informations de diagnostic

Utilisez l'algorithme génétique pour minimiser la fonction ps_example contrainte d'avoir une valeur entière x(1). La fonction ps_example est incluse lorsque vous exécutez cet exemple. Pour comprendre la raison pour laquelle le solveur s'est arrêté et comment ga a recherché un minimum, obtenez les résultats exitflag et output. Tracez également la valeur minimale observée de la fonction objectif à mesure que le solveur progresse.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
options = optimoptions('ga','PlotFcn', @gaplotbestf);
[x,fval,exitflag,output] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon,options)

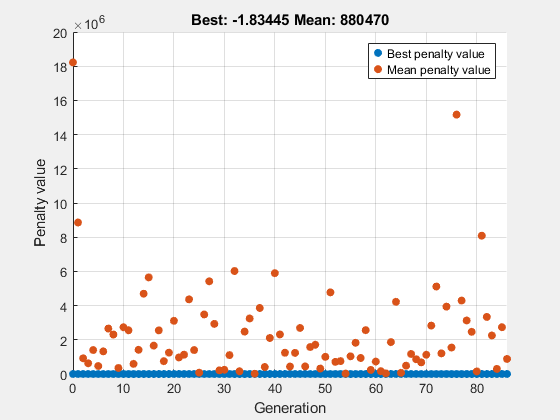
ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

x = 1×2

   -5.0000   -0.0834

fval = 
-1.8344

exitflag = 
1

output = struct with fields:
      problemtype: 'integerconstraints'
         rngstate: [1x1 struct]
      generations: 86
        funccount: 3311
          message: 'ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and ...'
    maxconstraint: 0
       hybridflag: []

Obtenir la population finale et les scores

Utilisez l'algorithme génétique pour minimiser la fonction ps_example contrainte d'avoir une valeur entière x(1). La fonction ps_example est incluse lorsque vous exécutez cet exemple. Obtenir toutes les sorties, y compris la population finale et le vecteur de scores.

intcon = 1;
rng default % For reproducibility
fun = @ps_example;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = [];
[x,fval,exitflag,output,population,scores] = ga(fun,2,A,b,Aeq,beq,lb,ub,nonlcon,intcon);

ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and 
the constraint violation is less than options.ConstraintTolerance.

Examinez les 10 premiers membres de la population finale et leurs scores correspondants. Notez que x(1) est une valeur entière pour tous ces membres de la population. L'algorithme entier ga génère uniquement des populations réalisables en nombres entiers.

disp(population(1:10,:))

   1.0e+03 *

   -0.0050   -0.0001
   -0.0050   -0.0001
   -1.6420    0.0027
   -1.5070    0.0010
   -0.4540    0.0104
   -0.2530   -0.0011
   -0.1210   -0.0003
   -0.1040    0.1314
   -0.0140   -0.0010
    0.0160   -0.0002

disp(scores(1:10))

   1.0e+06 *

   -0.0000
   -0.0000
    2.6798
    2.2560
    0.2016
    0.0615
    0.0135
    0.0099
    0.0001
    0.0000

Arguments d'entrée

fun — Fonction objectif

handle de fonction | nom de la fonction

Fonction objectif, spécifiée comme un handle de fonction ou un nom de fonction. Écrivez la fonction objectif pour accepter un vecteur de ligne de longueur nvars et renvoyer une valeur scalaire.

Lorsque l'option 'UseVectorized' est true, écrivez fun pour accepter une matrice pop par nvars, où pop est la taille de la population actuelle. Dans ce cas, fun renvoie un vecteur de la même longueur que pop contenant les valeurs de la fonction fitness. Assurez-vous que fun ne prend pas de taille particulière pour pop, puisque ga peut transmettre un seul membre d'une population même dans un calcul vectorisé.

Exemple : fun = @(x)(x-[4,2]).^2

Types de données : char | function_handle | string

nvars — Nombre de variables

entier positif

Nombre de variables, spécifié sous la forme d'un entier positif. Le solveur transmet des vecteurs de lignes de longueur nvars à fun.

Exemple : 4

Types de données : double

A — Contraintes d'inégalités linéaires

matrice réelle

Contraintes d'inégalités linéaires, spécifiées sous forme de matrice réelle. A est une matrice M par nvars, où M est le nombre d'inégalités.

A encode les inégalités linéaires M

A*x <= b,

où x est le vecteur colonne de nvars variables x(:), et b est un vecteur colonne avec M éléments.

Par exemple, pour préciser

x₁ + 2 x₂ ≤ 10
3 x₁ + 4 x₂ ≤ 20
5 x₁ + 6 x₂ ≤ 30,

donnez ces contraintes :

A = [1,2;3,4;5,6];
b = [10;20;30];

Exemple : Pour spécifier que la somme des variables de contrôle est égale à 1 ou moins, donnez les contraintes A = ones(1,N) et b = 1.

Types de données : double

b — Contraintes d'inégalités linéaires

vecteur réel

Contraintes d'inégalité linéaire, spécifiées comme un vecteur réel. b est un vecteur d'éléments M lié à la matrice A. Si vous passez b comme vecteur de ligne, les solveurs convertissent en interne b en vecteur de colonne b(:).

b encode les inégalités linéaires M

A*x <= b,

où x est le vecteur colonne de N variables x(:), et A est une matrice de taille M-par-N.

Par exemple, pour préciser

x₁ + 2 x₂ ≤ 10
3 x₁ + 4 x₂ ≤ 20
5 x₁ + 6 x₂ ≤ 30,

donnez ces contraintes :

A = [1,2;3,4;5,6];
b = [10;20;30];

Exemple : Pour spécifier que la somme des variables de contrôle est égale à 1 ou moins, donnez les contraintes A = ones(1,N) et b = 1.

Types de données : double

Aeq — Contraintes d'égalité linéaire

matrice réelle

Contraintes d'égalité linéaire, spécifiées sous forme de matrice réelle. Aeq est une matrice Me par nvars, où Me est le nombre d'égalités.

Aeq encode les égalités linéaires Me

Aeq*x = beq,

où x est le vecteur colonne de N variables x(:), et beq est un vecteur colonne avec Me éléments.

Par exemple, pour préciser

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

donnez ces contraintes :

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Exemple : Pour spécifier que la somme des variables de contrôle est égale à 1, donnez les contraintes Aeq = ones(1,N) et beq = 1.

Types de données : double

beq — Contraintes d'égalité linéaire

vecteur réel

Contraintes d'égalité linéaire, spécifiées comme un vecteur réel. beq est un vecteur d'éléments Me lié à la matrice Aeq. Si vous passez beq comme vecteur de ligne, les solveurs convertissent en interne beq en vecteur de colonne beq(:).

beq encode les égalités linéaires Me

Aeq*x = beq,

où x est le vecteur colonne de N variables x(:), et Aeq est une matrice de taille Meq-par-N.

Par exemple, pour préciser

x₁ + 2 x₂ + 3 x₃ = 10
2 x₁ + 4 x₂ + x₃ = 20,

donnez ces contraintes :

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Exemple : Pour spécifier que la somme des variables de contrôle est égale à 1, donnez les contraintes Aeq = ones(1,N) et beq = 1.

Types de données : double

lb — Limites inférieures

[] (par défaut) | vecteur ou tableau réel

Bornes inférieures, spécifiées sous la forme d'un vecteur réel ou d'un tableau de doubles. lb représente les bornes inférieures élément par élément dans lb ≤ x ≤ ub.

En interne, ga convertit un tableau lb en vecteur lb(:).

Exemple : lb = [0;-Inf;4] signifie x(1) ≥ 0, x(3) ≥ 4.

Types de données : double

ub — Limites supérieures

[] (par défaut) | vecteur ou tableau réel

Limites supérieures, spécifiées sous la forme d'un vecteur réel ou d'un tableau de doubles. ub représente les limites supérieures élément par élément dans lb ≤ x ≤ ub.

En interne, ga convertit un tableau ub en vecteur ub(:).

Exemple : ub = [Inf;4;10] signifie x(2) ≤ 4, x(3) ≤ 10.

Types de données : double

nonlcon — Contraintes non linéaires

handle de fonction | nom de la fonction

Contraintes non linéaires, spécifiées sous forme de handle de fonction ou de nom de fonction. nonlcon est une fonction qui accepte un vecteur ou un tableau x et renvoie deux tableaux, c(x) et ceq(x).

• c(x) est le tableau des contraintes d'inégalité non linéaires à x. ga tente de satisfaire

  c(x) <= 0

  pour toutes les entrées de c.

• ceq(x) est le tableau des contraintes d'égalité non linéaires à x. ga tente de satisfaire

  ceq(x) = 0

  pour toutes les entrées de ceq.

Par exemple,

x = ga(@myfun,4,A,b,Aeq,beq,lb,ub,@mycon)

où mycon est une fonction MATLAB^® telle que

function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.

Pour plus d'informations, voir Nonlinear Constraints.

Pour savoir comment utiliser les contraintes vectorisées, voir Vectorized Constraints.

Remarque

ga n'impose pas de contraintes non linéaires à satisfaire lorsque l'option PopulationType est définie sur 'bitString' ou 'custom'.

Si intcon n'est pas vide, la deuxième sortie de nonlcon (ceq) doit être une entrée vide ([]).

Pour plus d'informations sur la façon dont ga utilise nonlcon, voir Algorithmes de résolution de contraintes non linéaires pour algorithmes génétiques.

Types de données : char | function_handle | string

options — Options d'optimisation

sortie de optimoptions | structure

Options d'optimisation, spécifiées comme sortie de optimoptions ou d'une structure.

optimoptions masque les options répertoriées en italique. Voir Options that optimoptions Hides.

• Les valeurs dans {} indiquent la valeur par défaut.

• {}* représente la valeur par défaut lorsqu'il y a des contraintes linéaires, et pour MutationFcn également lorsqu'il y a des limites.

• I* indique la valeur par défaut pour les contraintes d'entiers ou indique des considérations spéciales pour les contraintes d'entiers.

• NM indique que l'option ne s'applique pas à gamultiobj.

Options pour ga et gamultiobj

Option	Description	Valeurs
ConstraintTolerance	Détermine la faisabilité par rapport aux contraintes non linéaires. De plus, max(sqrt(eps),ConstraintTolerance) détermine la faisabilité par rapport aux contraintes linéaires. Pour une structure d'options, utilisez TolCon.	Scalaire non négatif | {1e-3}
CreationFcn	Fonction qui crée la population initiale. Spécifier comme nom d'une fonction de création intégrée ou d'un handle de fonction. Voir Population Options.	{'gacreationuniform'} | {'gacreationlinearfeasible'}* | 'gacreationnonlinearfeasible' | {'gacreationuniformint'}I* pour ga | {'gacreationsobol'}I* pour gamultiobj | Fonction de création personnalisée
CrossoverFcn	Fonction que l'algorithme utilise pour créer des enfants issus de croisement. Spécifiez comme nom d'une fonction de croisement intégrée ou d'un handle de fonction. Voir Crossover Options.	{'crossoverscattered'} pour ga, {'crossoverintermediate'}* pour gamultiobj | {'crossoverlaplace'}I* | 'crossoverheuristic' | 'crossoversinglepoint' | 'crossovertwopoint' | 'crossoverarithmetic' | Fonction de croisement personnalisée
CrossoverFraction	La fraction de la population de la génération suivante, sans compter les enfants élites, que crée la fonction de croisement.	Scalaire non négatif | {0.8}
Display	Niveau d'affichage.	'off' | 'iter' | 'diagnose' | {'final'}
DistanceMeasureFcn	Fonction qui calcule la mesure de distance des individus. Spécifier comme nom d'une fonction de mesure de distance intégrée ou d'un handle de fonction. La valeur s'applique à la variable de décision ou à l'espace de conception (génotype) ou à l'espace de fonction (phénotype). La valeur par défaut 'distancecrowding' se trouve dans l'espace fonctionnel (phénotype). Pour gamultiobj uniquement. Voir Multiobjective Options. Pour une structure d'options, utilisez un handle de fonction, pas un nom.	{'distancecrowding'} signifie la même chose que {@distancecrowding,'phenotype'} | {@distancecrowding,'genotype'} | Fonction de distance personnalisée
EliteCount	NM Entier positif spécifiant combien d'individus de la génération actuelle sont assurés de survivre à la génération suivante. Non utilisé dans gamultiobj.	Entier non négatif | {ceil(0.05*PopulationSize)} | {0.05*(default PopulationSize)} pour les problèmes d'entiers mixtes
FitnessLimit	NM Si la fonction fitness atteint la valeur de FitnessLimit, l'algorithme s'arrête.	Scalaire | {-Inf}
FitnessScalingFcn	Fonction qui met à l'échelle les valeurs de la fonction fitness. Spécifiez comme nom d'une fonction de mise à l'échelle intégrée ou d'un handle de fonction. Option indisponible pour gamultiobj.	{'fitscalingrank'} | 'fitscalingshiftlinear' | 'fitscalingprop' | 'fitscalingtop' | Fonction de mise à l'échelle de la condition physique personnalisée
FunctionTolerance	L'algorithme s'arrête si la variation relative moyenne de la valeur de la meilleure fonction fitness sur MaxStallGenerations générations est inférieure ou égale à FunctionTolerance. Si StallTest est 'geometricWeighted', alors l'algorithme s'arrête si la variation relative moyenne pondérée est inférieure ou égale à FunctionTolerance. Pour gamultiobj, l'algorithme s'arrête lorsque la moyenne géométrique de la variation relative de la valeur de l'écart sur options.MaxStallGenerations générations est inférieure à options.FunctionTolerance, et l'écart final est inférieur à l'écart moyen sur les options.MaxStallGenerations générations passées. Voir gamultiobj Algorithm. Pour une structure d'options, utilisez TolFun.	Scalaire non négatif | {1e-6} pour ga, {1e-4} pour gamultiobj
HybridFcn	I* Fonction qui continue l'optimisation après la fin de ga. Spécifier comme un nom ou un handle de fonction. Alternativement, un cell array spécifiant la fonction hybride et ses options. Voir ga Hybrid Function. Pour gamultiobj, la seule fonction hybride est @fgoalattain. Voir gamultiobj Hybrid Function. Lorsque le problème comporte des contraintes entières, vous ne pouvez pas utiliser de fonction hybride. Voir Quand utiliser une fonction hybride.	Nom de la fonction ou handle | 'fminsearch' | 'patternsearch' | 'fminunc' | 'fmincon' | {[]} ou cell array 1 par 2 | {@solver, hybridoptions}, où solver = fminsearch, patternsearch, fminunc ou fmincon {[]}
InitialPenalty	NM I* Valeur initiale du paramètre de pénalité	Scalaire positif | {10}
InitialPopulationMatrix	Population initiale utilisée pour amorcer l'algorithme génétique. Contient jusqu'à PopulationSize lignes et N colonnes, où N est le nombre de variables. Vous pouvez transmettre une population partielle, c'est-à-dire une population contenant moins de PopulationSize lignes. Dans ce cas, l’algorithme génétique utilise CreationFcn pour générer les membres restants de la population. Voir Population Options. Pour une structure d'options, utilisez InitialPopulation.	Matrice | {[]}
InitialPopulationRange	Matrice ou vecteur spécifiant l'étendue des individus de la population initiale. S'applique à la fonction de création gacreationuniform. ga décale et met à l'échelle la plage initiale par défaut pour correspondre à toutes les limites finies. Pour une structure d'options, utilisez PopInitRange.	Matrice ou vecteur | {[-10;10]} pour les composants non bornés, {[-1e4+1;1e4+1]} pour les composants non bornés des problèmes à contraintes entières, {[lb;ub]} pour les composants bornés, avec la plage par défaut modifiée pour correspondre aux limites unilatérales
InitialScoresMatrix	Les scores initiaux sont utilisés pour déterminer la condition physique. Contient jusqu'à PopulationSize lignes et Nf colonnes, où Nf est le nombre de fonctions fitness (1 pour ga, supérieur à 1 pour gamultiobj). Vous pouvez transmettre une matrice de scores partiels, c'est-à-dire une matrice contenant moins de PopulationSize lignes. Dans ce cas, le solveur renseigne les scores lorsqu'il évalue les fonctions fitness. Pour une structure d'options, utilisez InitialScores.	Vecteur colonne pour objectif unique | matrice pour multi-objectifs | {[]}
MaxGenerations	Nombre maximal d'itérations avant l'arrêt de l'algorithme. Pour une structure d'options, utilisez Generations.	Entier non négatif |{100*numberOfVariables} pour ga, {200*numberOfVariables} pour gamultiobj
MaxStallGenerations	L'algorithme s'arrête si la variation relative moyenne de la valeur de la meilleure fonction fitness sur MaxStallGenerations générations est inférieure ou égale à FunctionTolerance. Si StallTest est 'geometricWeighted', alors l'algorithme s'arrête si la variation relative moyenne pondérée est inférieure ou égale à FunctionTolerance. Pour gamultiobj, l'algorithme s'arrête lorsque la moyenne géométrique de la variation relative de la valeur de l'écart sur options.MaxStallGenerations générations est inférieure à options.FunctionTolerance, et l'écart final est inférieur à l'écart moyen sur les options.MaxStallGenerations générations passées. Voir gamultiobj Algorithm. Pour une structure d'options, utilisez StallGenLimit.	Entier non négatif | {50} pour ga, {100} pour gamultiobj
MaxStallTime	NM L'algorithme s'arrête s'il n'y a pas d'amélioration de la fonction objectif pendant MaxStallTime secondes, comme mesuré par tic et toc. Pour une structure d'options, utilisez StallTimeLimit.	Scalaire positif | {Inf}
MaxTime	L'algorithme s'arrête après avoir fonctionné pendant MaxTime secondes, comme mesuré par tic et toc. Cette limite est appliquée après chaque itération, donc ga peut dépasser la limite lorsqu'une itération prend beaucoup de temps. Pour une structure d'options, utilisez TimeLimit.	Scalaire non négatif | {Inf}
MigrationDirection	Direction de la migration. Voir Migration Options.	'both' | {'forward'}
MigrationFraction	Scalaire de 0 à 1 spécifiant la fraction d'individus dans chaque sous-population qui migre vers une sous-population différente. Voir Migration Options.	Scalaire | {0.2}
MigrationInterval	Entier positif spécifiant le nombre de générations qui ont lieu entre les migrations d'individus entre sous-populations. Voir Migration Options.	Entier positif | {20}
MutationFcn	Fonction qui produit des enfants issus de mutation. Spécifier comme nom d'une fonction de mutation intégrée ou d'un handle de fonction. Voir Mutation Options.	{'mutationgaussian'} pour ga sans contraintes | {'mutationadaptfeasible'}* pour gamultiobj et pour ga avec contraintes | {'mutationpower'}I* | 'mutationpositivebasis' | 'mutationuniform' | Fonction de mutation personnalisée
NonlinearConstraintAlgorithm	Algorithme de contrainte non linéaire. Voir Algorithmes de résolution de contraintes non linéaires pour algorithmes génétiques. Option inchangeable pour gamultiobj. Pour une structure d'options, utilisez NonlinConAlgorithm.	{'auglag'} pour ga, {'penalty'} pour gamultiobj
OutputFcn	Fonctions que ga appelle à chaque itération. Spécifiez comme un handle de fonction ou un cell array de handles de fonction. Voir Output Function Options. Pour une structure d'options, utilisez OutputFcns.	Handle de fonction ou cell array de handles de fonction | {[]}
ParetoFraction	Scalaire de 0 à 1 spécifiant la fraction d'individus à conserver sur le premier front de Pareto tandis que le solveur sélectionne les individus des fronts supérieurs, pour gamultiobj uniquement. Voir Multiobjective Options.	Scalaire | {0.35}
PenaltyFactor	NM I* Paramètre de mise à jour de pénalité.	Scalaire positif | {100}
PlotFcn	Fonction qui trace les données calculées par l'algorithme. Spécifiez comme nom d'une fonction de tracé intégrée, d'un handle de fonction ou d'un cell array de noms prédéfinis ou de handles de fonction. Voir Plot Options. Pour une structure d'options, utilisez PlotFcns.	ga ou gamultiobj : {[]} | 'gaplotdistance' | 'gaplotgenealogy' | 'gaplotselection' | 'gaplotscorediversity' |'gaplotscores' | 'gaplotstopping' | 'gaplotmaxconstr' | Fonction de tracé personnalisée ga uniquement : 'gaplotbestf' | 'gaplotbestindiv' | 'gaplotexpectation' | 'gaplotrange' gamultiobj uniquement : 'gaplotpareto' | 'gaplotparetodistance' | 'gaplotrankhist' | 'gaplotspread'
PlotInterval	Entier positif spécifiant le nombre de générations entre les appels consécutifs aux fonctions de tracé.	Entier positif | {1}
PopulationSize	Taille de la population.	Entier positif | {50} lorsque numberOfVariables <= 5, {200} sinon | {min(max(10*nvars,40),100)} pour les problèmes d'entiers mixtes
PopulationType	Type de données de la population. Doit être 'doubleVector' pour les problèmes d'entiers mixtes.	'bitstring' | 'custom' | {'doubleVector'} la ga ignore toutes les contraintes lorsque PopulationType est défini sur 'bitString' ou 'custom'. Voir Population Options.
SelectionFcn	Fonction qui sélectionne les parents des enfants issus de croisement et issus de mutation. Spécifier comme nom d'une fonction de sélection intégrée ou d'un handle de fonction. gamultiobj utilise uniquement 'selectiontournament'.	{'selectionstochunif'} pour ga, {'selectiontournament'} pour gamultiobj | 'selectionremainder' | 'selectionuniform' | 'selectionroulette' | Fonction de sélection personnalisée
StallTest	Type de test d'arrêt NM.	'geometricWeighted' | {'averageChange'}
UseParallel	Calculez les fonctions fitness et de contraintes non linéaires en parallèle. Voir Vectorize and Parallel Options (User Function Evaluation) et How to Use Parallel Processing in Global Optimization Toolbox.	true | {false}
UseVectorized	Spécifie si les fonctions sont vectorisées. Voir Vectorize and Parallel Options (User Function Evaluation) et Vectorize the Fitness Function. Pour une structure d'options, utilisez Vectorized avec les valeurs 'on' ou 'off'.	true | {false}

Exemple : optimoptions('ga','PlotFcn',@gaplotbestf)

intcon — Variables de type entier

vecteur d'entiers positifs

Variables entières, spécifiées comme un vecteur d'entiers positifs prenant des valeurs de 1 à nvars. Chaque valeur dans intcon représente un composant x qui a une valeur entière.

Remarque

Lorsque intcon n'est pas vide, nonlcon doit renvoyer vide pour ceq. Pour plus d'informations sur la programmation en nombres entiers, voir Mixed Integer ga Optimization.

Exemple : Pour spécifier que les entrées paires dans x ont des valeurs entières, définissez intcon sur 2:2:nvars

Types de données : double

problem — Description du problème

structure

Description du problème, spécifiée sous la forme d'une structure contenant ces champs.

fitnessfcn	Fonctions fitness
nvars	Nombre de variables du design
Aineq	Matrice A pour les contraintes d'inégalités linéaires
Bineq	Vecteur b pour les contraintes d'inégalité linéaire
Aeq	Matrice Aeq pour les contraintes d'égalité linéaire
Beq	Vecteur beq pour les contraintes d'égalité linéaire
lb	Borne inférieure sur x
ub	Borne supérieure sur x
nonlcon	Fonctions de contrainte non linéaires
intcon	Indices des variables de type entier
rngstate	Champ pour réinitialiser l'état du générateur de nombres aléatoires
solver	'ga'
options	Options créées à l'aide de optimoptions ou d'une structure d'options

Vous devez spécifier les champs fitnessfcn, nvars et options. Le reste est facultatif pour ga.

Types de données : struct

Arguments de sortie

x — Solution

vecteur réel

Solution, renvoyée sous forme de vecteur réel. x est le meilleur point que ga a localisé au cours de ses itérations.

fval — Valeur de la fonction objectif lors de la solution

nombre réel

Valeur de la fonction objectif à la solution, renvoyée sous forme de nombre réel. Généralement, fval = fun(x).

exitflag — Raison pour laquelle ga s'est arrêté

entier

Raison pour laquelle ga s'est arrêté, renvoyée sous forme d'entier.

Exit Flag	Signification
1	Sans contraintes non linéaires — La variation cumulative moyenne de la valeur de la fonction fitness sur MaxStallGenerations générations est inférieure à FunctionTolerance et la violation de contrainte est inférieure à ConstraintTolerance.
	Avec des contraintes non linéaires — La magnitude de la mesure de complémentarité (voir Mesure de complémentarité) est inférieure à sqrt(ConstraintTolerance), le sous-problème est résolu en utilisant une tolérance inférieure à FunctionTolerance et la violation de contrainte est inférieure à ConstraintTolerance.
3	La valeur de la fonction fitness n'a pas changé en MaxStallGenerations générations et la violation de contrainte est inférieure à ConstraintTolerance.
4	L'ampleur du pas est inférieure à la précision de la machine et la violation de contrainte est inférieure à ConstraintTolerance.
5	La limite de fitness minimale FitnessLimit est atteinte et la violation de contrainte est inférieure à ConstraintTolerance.
0	Nombre maximal de générations MaxGenerations dépassé.
-1	Optimisation terminée par une fonction de sortie ou une fonction de tracé.
-2	Aucun point possible n'a été trouvé.
-4	La limite de temps de Stall Time MaxStallTime a été dépassée.
-5	Délai MaxTime dépassé.

Lorsqu'il existe des contraintes d'entier, ga utilise la valeur d'aptitude de pénalité au lieu de la valeur d'aptitude pour les critères d'arrêt.

output — Informations sur le processus d'optimisation

structure

Informations sur le processus d'optimisation, renvoyées sous forme de structure avec ces champs :

• problemtype — Type de problème, l'un des suivants :

  • 'unconstrained'

  • 'boundconstraints'

  • 'linearconstraints'

  • 'nonlinearconstr'

  • 'integerconstraints'

• rngstate — État du générateur de nombres aléatoires MATLAB, juste avant le démarrage de l'algorithme. Vous pouvez utiliser les valeurs de rngstate pour reproduire la sortie de ga. Voir Reproduce Results.

• generations — Nombre de générations calculées.

• funccount — Nombre d’évaluations de la fonction fitness.

• message — Raison pour laquelle l’algorithme s’est terminé.

• maxconstraint — Violation de contrainte maximale, le cas échéant.

• hybridflag — Exit flag de la fonction hybride. Concerne les options HybridFcn. Non applicable à gamultiobj.

population — Population finale

matrice

Population finale, renvoyée sous forme de matrice PopulationSize-par-nvars. Les lignes de population sont les individus.

scores — Résultats finaux

vecteur de colonne

Scores finaux, renvoyés sous forme de vecteur colonne.

• Pour les problèmes non entiers, les scores finaux sont les valeurs de la fonction fitness des lignes de population.

• Pour les problèmes entiers, les scores finaux sont les valeurs de fitness de pénalité des membres de la population. Voir Integer ga Algorithm.

En savoir plus

Mesure de complémentarité

Dans le solveur de contraintes non linéaires lagrangiennes augmentées, la mesure de complémentarité est la norme du vecteur dont les éléments sont c_iλ_i, où c_i est la violation de contrainte d'inégalité non linéaire et λ_i est le multiplicateur de Lagrange correspondant. Voir Algorithme génétique lagrangien augmenté.

Conseils

• Pour écrire une fonction avec des paramètres supplémentaires aux variables indépendantes qui peuvent être appelées par ga, voir Passing Extra Parameters.

• Pour les problèmes qui utilisent le type de population Double Vector (par défaut), ga n'accepte pas les fonctions dont les entrées sont de type complex. Pour résoudre des problèmes impliquant des données complexes, écrivez vos fonctions de manière à ce qu'elles acceptent des vecteurs réels, en séparant les parties réelles et imaginaires.

Algorithmes

Pour une description de l'algorithme génétique, voir Comment fonctionne l'algorithme génétique.

Pour une description de l'algorithme de programmation en nombres entiers mixtes, voir Integer ga Algorithm.

Pour une description des algorithmes de contraintes non linéaires, voir Algorithmes de résolution de contraintes non linéaires pour algorithmes génétiques.

Fonctionnalités alternatives

Application

La tâche Optimize du Live Editor fournit une interface visuelle pour ga.

Références

[1] Goldberg, David E., Genetic Algorithms in Search, Optimization & Machine Learning, Addison-Wesley, 1989.

[2] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds”, SIAM Journal on Numerical Analysis, Volume 28, Number 2, pages 545–572, 1991.

[3] A. R. Conn, N. I. M. Gould, and Ph. L. Toint. “A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds”, Mathematics of Computation, Volume 66, Number 217, pages 261–288, 1997.

Capacités étendues

Automatic Parallel Support

Accélérez le code en exécutant plusieurs calculs en parallèle avec Parallel Computing Toolbox™.

Pour exécuter en parallèle, définissez l'option 'UseParallel' sur true.

options = optimoptions('solvername','UseParallel',true)

Pour plus d'informations, voir How to Use Parallel Processing in Global Optimization Toolbox.

Historique des versions

Introduit avant R2006a

R2019b: ga effectue moins d'évaluations de la fonction fitnesss

Lorsque la fonction fitness est déterministe, ga ne réévalue pas la fonction fitness sur les individus d'élite (les meilleurs actuellement). Vous pouvez contrôler ce comportement en accédant au nouveau champ state.EvalElites et en le modifiant dans une fonction de sortie personnalisée ou une fonction de tracé personnalisée. De même, lorsque la population initiale comporte des membres en double, ga évalue chaque membre unique une seule fois. Vous pouvez contrôler ce comportement dans une fonction de sortie personnalisée ou une fonction de tracé personnalisée en accédant au nouveau champ state.HaveDuplicates et en le modifiant. Pour plus de détails, voir Custom Output Function for Genetic Algorithm ou Fonction de tracé personnalisée.

Pour plus de détails sur les deux nouveaux champs, voir The State Structure.

Voir aussi

gamultiobj | optimoptions | particleswarm | patternsearch | Optimize

Rubriques

• Algorithme génétique
• Commencer avec Global Optimization Toolbox
• Configuration du problème d'optimisation basé sur le solveur