Multiple Solutions
About Multiple Solutions
You obtain multiple solutions in an object by calling run with
the syntax
[x,fval,exitflag,output,manymins] = run(...);
manymins is a vector of solution objects; see GlobalOptimSolution. The manymins vector is in
order of objective function value, from lowest (best) to highest (worst). Each
solution object contains the following properties (fields):
X— a local minimumFval— the value of the objective function atXExitflag— the exit flag for the local solver (described in the local solver function reference page:fminconexitflag,fminuncexitflag,lsqcurvefitexitflag, orlsqnonlinexitflagOutput— an output structure for the local solver (described in the local solver function reference page:fminconoutput,fminuncoutput,lsqcurvefitoutput, orlsqnonlinoutputX0— a cell array of start points that led to the solution pointX
Note
manymins contains only those solutions corresponding to
positive local solver exit flags. If you want to collect all the local
solutions, not only the ones corresponding to positive exit flags, use the
@savelocalsolutions output function. See Output Functions for GlobalSearch and MultiStart.
There are several ways to examine the vector of solution objects:
In the MATLAB® Workspace panel. Double-click the solution object.

Using dot notation.
GlobalOptimSolutionproperties are capitalized. Use proper capitalization to access the properties.For example, to find the vector of function values, enter:
fcnvals = [manymins.Fval]
fcnvals = -1.0316 -0.2155 0
To get a cell array of all the start points that led to the lowest function value (the first element of
manymins), enter:smallX0 = manymins(1).X0;
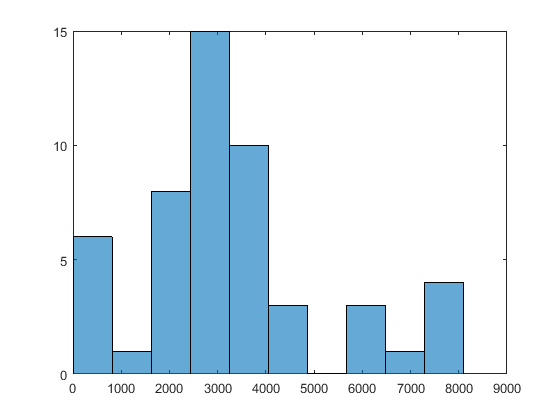
Plot some field values. For example, to see the range of resulting
Fval, enter:histogram([manymins.Fval],10)
This results in a histogram of the computed function values. (The figure shows a histogram from a different example than the previous few figures.)
Change the Definition of Distinct Solutions
You might find out, after obtaining multiple local solutions,
that your tolerances were not appropriate. You can have many more
local solutions than you want, spaced too closely together. Or you
can have fewer solutions than you want, with GlobalSearch or MultiStart clumping
together too many solutions.
To deal with this situation, run the solver again with different
tolerances. The XTolerance and FunctionTolerance tolerances
determine how the solvers group their outputs into the GlobalOptimSolution vector.
These tolerances are properties of the GlobalSearch or MultiStart object.
For example, suppose you want to use the active-set algorithm
in fmincon to solve the problem in Example of Run with MultiStart. Further
suppose that you want to have tolerances of 0.01 for
both XTolerance and FunctionTolerance.
The run method groups local solutions whose objective
function values are within FunctionTolerance of
each other, and which are also less than XTolerance apart
from each other. To obtain the solution:
% Set the random stream to get exactly the same output % rng(14,'twister') ms = MultiStart('FunctionTolerance',0.01,'XTolerance',0.01); opts = optimoptions(@fmincon,'Algorithm','active-set'); sixmin = @(x)(4*x(1)^2 - 2.1*x(1)^4 + x(1)^6/3 ... + x(1)*x(2) - 4*x(2)^2 + 4*x(2)^4); problem = createOptimProblem('fmincon','x0',[-1,2],... 'objective',sixmin,'lb',[-3,-3],'ub',[3,3],... 'options',opts); [xminm,fminm,flagm,outptm,someminsm] = run(ms,problem,50);
MultiStart completed the runs from all start points. All 50 local solver runs converged with a positive local solver exit flag.
someminsm
someminsm =
1x5 GlobalOptimSolution
Properties:
X
Fval
Exitflag
Output
X0In this case, MultiStart generated five distinct
solutions. Here “distinct” means that the solutions
are more than 0.01 apart in either objective function value or location.