Tracer un front de Pareto 3D
Cet exemple montre comment tracer un front de Pareto pour trois objectifs. Chaque fonction objectif est la distance au carré à partir d'un point 3D particulier. Pour accélérer le calcul, écrivez chaque fonction objectif de manière vectorisée sous forme de produit scalaire. Pour obtenir un ensemble de solutions dense, utilisez 200 points sur le front de Pareto.
L'exemple montre d'abord comment obtenir le tracé à l'aide de la fonction de tracé intégrée 'psplotparetof'. Résolvez ensuite le même problème et obtenez le tracé en utilisant gamultiobj, ce qui nécessite des paramètres d’options légèrement différents. L'exemple montre comment obtenir des variables de solution pour un point particulier dans le diagramme de Pareto. L'exemple montre ensuite comment tracer les points directement, sans utiliser de fonction de tracé, et montre comment tracer une surface interpolée au lieu de points de Pareto.
fun = @(x)[dot(x - [1,2,3],x - [1,2,3],2), ... dot(x - [-1,3,-2],x - [-1,3,-2],2), ... dot(x - [0,-1,1],x - [0,-1,1],2)]; options = optimoptions('paretosearch','UseVectorized',true,'ParetoSetSize',200,... 'PlotFcn','psplotparetof'); lb = -5*ones(1,3); ub = -lb; rng default % For reproducibility [x,f] = paretosearch(fun,3,[],[],[],[],lb,ub,[],options);
Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
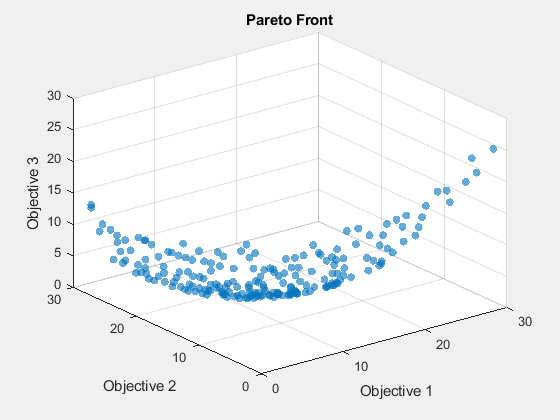
opts = optimoptions('gamultiobj',"PlotFcn","gaplotpareto","PopulationSize",200); [xg,fg] = gamultiobj(fun,3,[],[],[],[],lb,ub,[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

Ce graphique montre beaucoup moins de points que le graphique paretosearch. Résolvez à nouveau le problème en utilisant une population plus large.
opts.PopulationSize = 400; [xg,fg] = gamultiobj(fun,3,[],[],[],[],lb,ub,[],opts);
gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
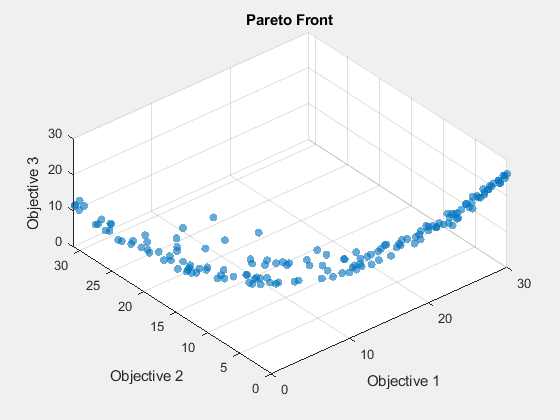
Modifiez l'angle de vue pour mieux correspondre au tracé psplotpareto.
view(-40,57)
Trouver un point de solution à l'aide des info-bulles
Sélectionnez un point dans le tracé à l’aide de l’outil Astuces de données.

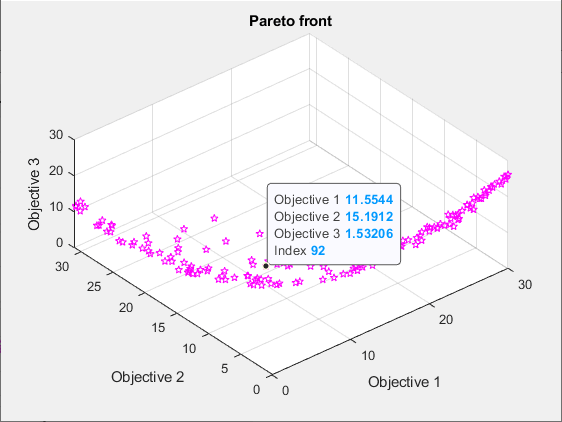
Le point représenté a l'index 92. Affichez le point xg(92,:) qui contient les variables de solution associées au point illustré.
disp(xg(92,:))
-0.2889 0.0939 0.4980
Évaluez les fonctions objectif à ce stade pour voir qu’elles correspondent aux valeurs affichées.
disp(fun(xg(92,:)))
11.5544 15.1912 1.5321
Créer un nuage de points en 3D
Tracez des points sur le front de Pareto en utilisant scatter3.
figure subplot(2,2,1) scatter3(f(:,1),f(:,2),f(:,3),'k.'); subplot(2,2,2) scatter3(f(:,1),f(:,2),f(:,3),'k.'); view(-148,8) subplot(2,2,3) scatter3(f(:,1),f(:,2),f(:,3),'k.'); view(-180,8) subplot(2,2,4) scatter3(f(:,1),f(:,2),f(:,3),'k.'); view(-300,8)
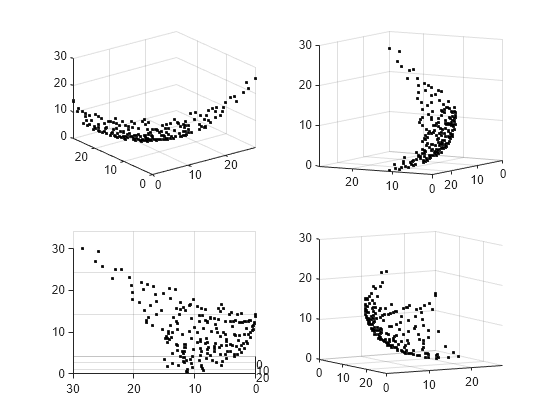
En faisant tourner le tracé de manière interactive, vous obtenez une meilleure vue de sa structure.
Graphique de surface interpolé
Pour voir le front de Pareto comme une surface, créez un interpolant dispersé.
figure F = scatteredInterpolant(f(:,1),f(:,2),f(:,3),'linear','none');
Pour tracer la surface résultante, créez un maillage dans l'espace x-y des valeurs les plus petites aux plus grandes. Tracez ensuite la surface interpolée.
sgr = linspace(min(f(:,1)),max(f(:,1))); ygr = linspace(min(f(:,2)),max(f(:,2))); [XX,YY] = meshgrid(sgr,ygr); ZZ = F(XX,YY);
Tracez les points de Pareto et la surface ensemble.
figure subplot(2,2,1) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off subplot(2,2,2) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off view(-148,8) subplot(2,2,3) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off view(-180,8) subplot(2,2,4) surf(XX,YY,ZZ,'LineStyle','none') hold on scatter3(f(:,1),f(:,2),f(:,3),'k.'); hold off view(-300,8)
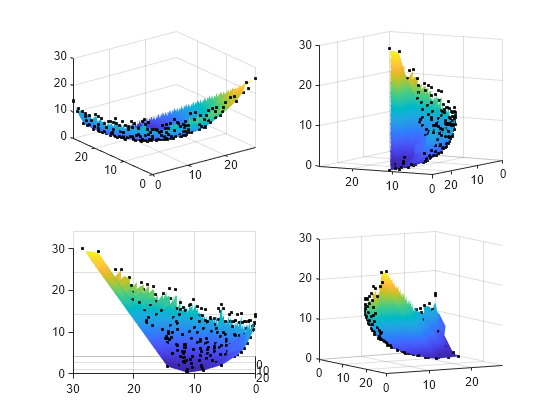
En faisant tourner le tracé de manière interactive, vous obtenez une meilleure vue de sa structure.
Tracer un ensemble de Pareto dans un espace de variables de contrôle
Vous pouvez obtenir un tracé des points sur l'ensemble de Pareto en utilisant la fonction de tracé 'psplotparetox'.
options.PlotFcn = 'psplotparetox';
[x,f] = paretosearch(fun,3,[],[],[],[],lb,ub,[],options);Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
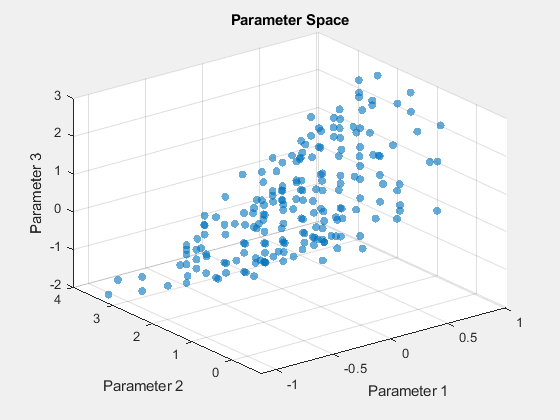
Vous pouvez également créer un nuage de points des valeurs x dans l’ensemble de Pareto.
figure subplot(2,2,1) scatter3(x(:,1),x(:,2),x(:,3),'k.'); subplot(2,2,2) scatter3(x(:,1),x(:,2),x(:,3),'k.'); view(-148,8) subplot(2,2,3) scatter3(x(:,1),x(:,2),x(:,3),'k.'); view(-180,8) subplot(2,2,4) scatter3(x(:,1),x(:,2),x(:,3),'k.'); view(-300,8)
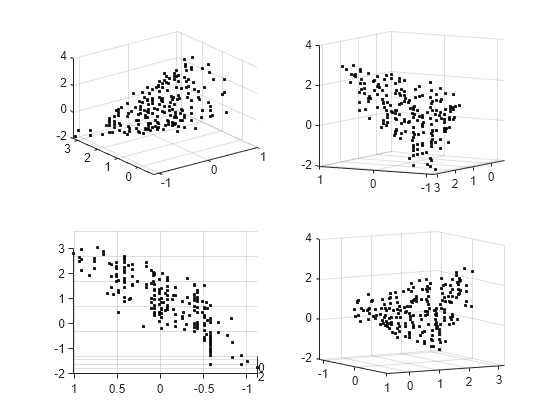
Cet ensemble n'a pas de surface transparente. En faisant tourner le tracé de manière interactive, vous obtenez une meilleure vue de sa structure.
Terrain parallèle
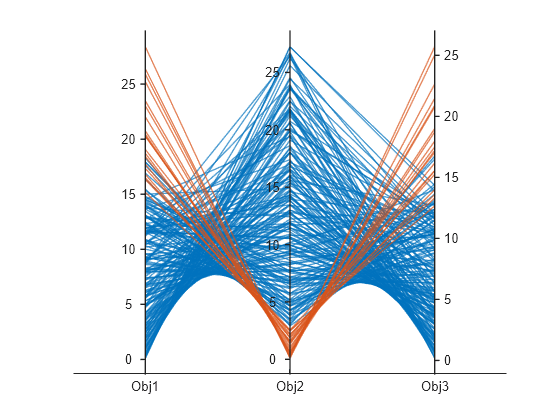
Vous pouvez tracer l'ensemble de Pareto à l'aide d'un tracé de coordonnées parallèles. Vous pouvez utiliser un tracé de coordonnées parallèles pour n’importe quel nombre de dimensions. Dans le graphique, chaque ligne colorée représente un point de Pareto et chaque variable de coordonnées est tracée sur une ligne verticale associée. Tracez les valeurs de la fonction objectif à l’aide de parellelplot.
figure p = parallelplot(f); p.CoordinateTickLabels =["Obj1";"Obj2";"Obj3"];
Coloriez les points de Pareto dans le dixième le plus bas des valeurs de Obj2.
minObj2 = min(f(:,2));
maxObj2 = max(f(:,2));
grpRng = minObj2 + 0.1*(maxObj2-minObj2);
grpData = f(:,2) <= grpRng;
p.GroupData = grpData;
p.LegendVisible = "off";