La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.
Transformer des données entre les domaines temporels et fréquentiels
System Identification Toolbox™ fournit des outils pour analyser les données et pour estimer et évaluer des modèles aussi bien dans les domaines temporel que fréquentiel. Pour utiliser des outils et des méthodes qui ne sont pas dans le même domaine que vos données mesurées, vous pouvez transformer vos données entre le domaine temporel et fréquentiel.
L’objet iddata stocke des données dans le domaine temporel ou dans le domaine fréquentiel.
Les données dans le domaine temporel sont composées d’une ou plusieurs variables d’entrée u(t) et d’une ou plusieurs variables de sortie y(t), échantillonnées en fonction du temps.
Les données dans le domaine fréquentiel sont composées soit de signaux transformés d’entrée et de sortie dans le domaine temporel, soit d’une réponse en fréquence du système échantillonnée en fonction de la fréquence variable indépendante.
Pour obtenir des informations détaillées sur la représentation de données dans le domaine temporel et dans le domaine fréquentiel dans MATLAB®, consultez Representing Data in MATLAB Workspace.
Vous pouvez transformer vos données d’un domaine à l’autre. Le tableau résume les commandes pour transformer les données entre les domaines temporels et fréquentiels. Pour plus d’informations sur les commandes, consultez les pages de référence sur les commandes correspondantes.
| Commande | Description | Exemple de syntaxe |
|---|---|---|
fft | Transformer des données dans le domaine temporel vers le domaine fréquentiel. Vous pouvez spécifier | Pour transformer l’objet f_data = fft(t_data,N) |
ifft | Transformer des données dans le domaine fréquentiel vers le domaine temporel. Les fréquences sont linéaires et espacées de manière égale. | Pour transformer l’objet t_data = ifft(f_data) |
Convertir des données iddata sous la forme d’une réponse en fréquence idfrd est un type d’estimation. Si vous souhaitez estimer la réponse en fréquence au moyen d’un objet iddata, consultez Transforming Between Frequency-Domain and Frequency-Response Data.
Transformer des données entre les domaines temporels et fréquentiels
Transformez des données du domaine temporel vers le domaine fréquentiel puis vers le domaine temporel, et comparez la performance estimée des modèles à partir des données originales et transformées.
Chargez et tracez les données dans le domaine temporel z1, contenant 300 échantillons.
load iddata1 z1 plot(z1)

Trouvez le pas d’échantillonnage Ts de z1.
Ts = z1.Ts
Ts = 0.1000
Le pas d’échantillonnage est de 0,1 s.
Transformez z1 dans le domaine fréquentiel.
z1f = fft(z1)
z1f =
Frequency domain data set with responses at 151 frequencies.
Frequency range: 0 to 31.416 rad/seconds
Sample time: 0.1 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
Data Properties
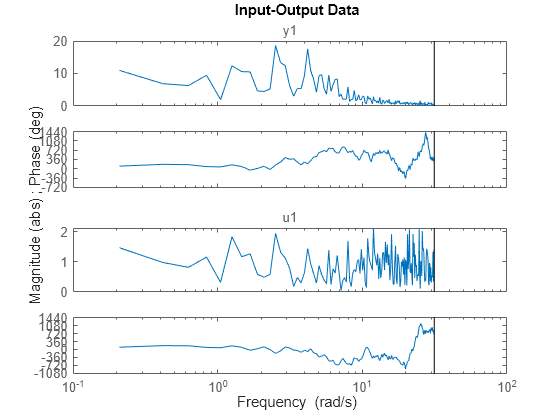
La plage de fréquences s’étend à 31,416 rad/s, ce qui est égal à la fréquence de Nyquist de pi/Ts.
Tracez les données dans le domaine fréquentiel.
plot(z1f)
Transformez z1f dans le domaine temporel et tracez les deux signaux dans le domaine temporel en même temps.
z1t = ifft(z1f)
z1t =
Time domain data set with 300 samples.
Sample time: 0.1 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
Data Properties
plot(z1t,z1)
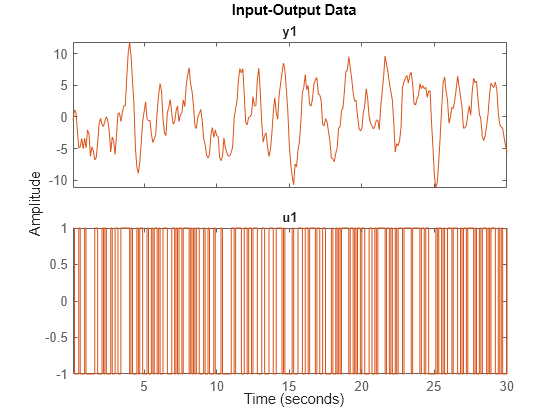
Les signaux s’alignent précisément.
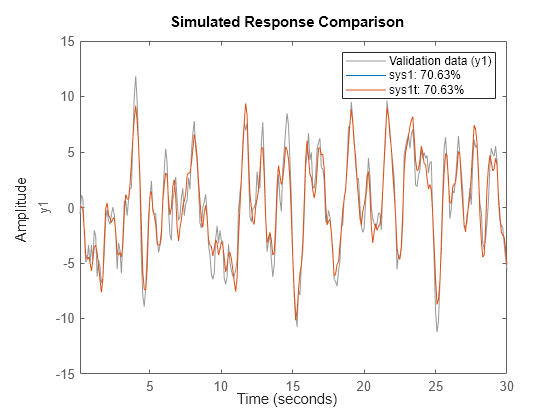
Estimez des modèles de représentation d’état de second ordre pour z1 et z1t.
sys1 = ssest(z1,2); sys1t = ssest(z1t,2); compare(z1,sys1,sys1t)
Estimez un modèle de représentation d’état pour z1f.
sys1f = ssest(z1f,2); compare(z1f,sys1f)
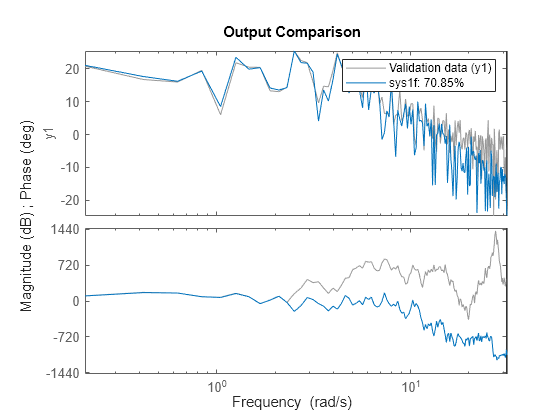
Les pourcentages d’ajustement pour les modèles dans le domaine temporel et dans le domaine fréquentiel sont similaires.
Voir aussi
fft | iddata | ifft | etfe | spa | spafdr