nufft
Nonuniform fast Fourier transform
Description
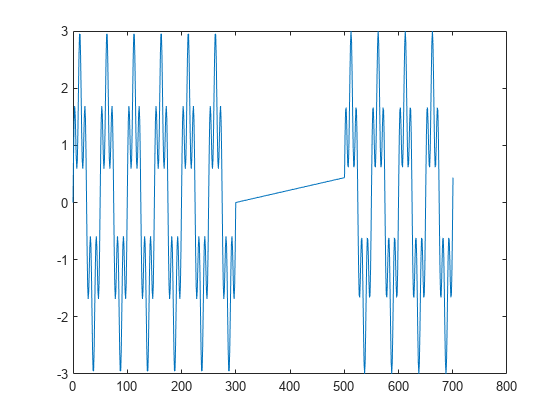
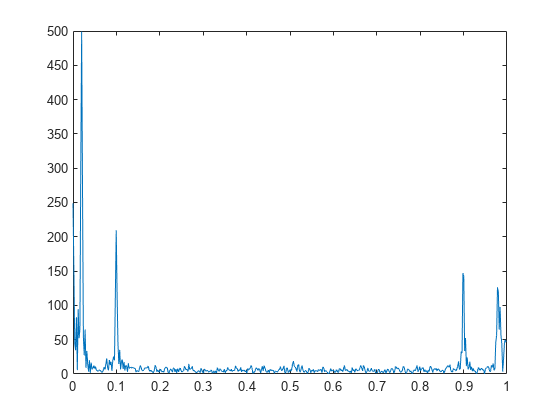
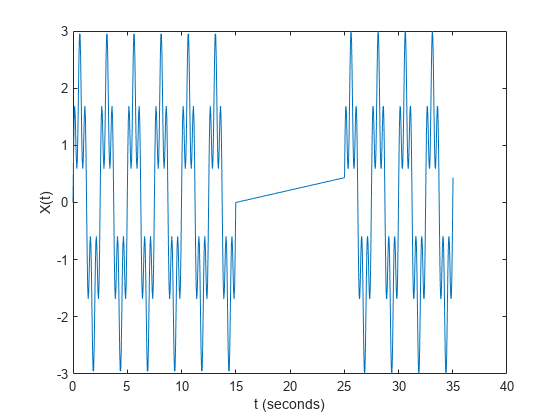
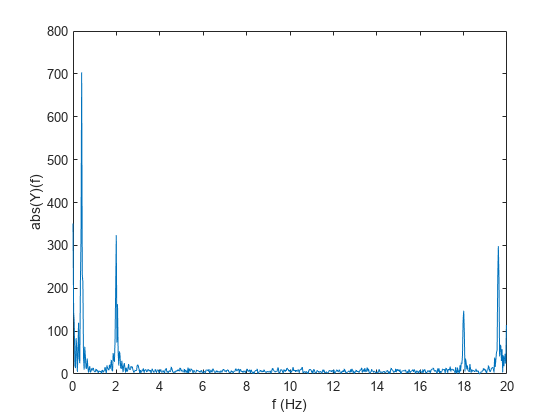
Y = nufft(X,t)X using the sample points
t.
If
Xis a vector, thennufftreturns the transform of the vector.If
Xis a matrix, thennuffttreats the columns ofXas vectors and returns the transform of each column.If
Xis a multidimensional array, thennuffttreats the values along the first array dimension whose size does not equal 1 as vectors and returns the transform of each vector.
Y = nufft(X)X, and is equivalent to
fft(X).
Examples
Input Arguments
More About
References
[1] Potter, Samuel F., Nail A. Gumerov, and Ramani Duraiswami. “Fast Interpolation of Bandlimited Functions.” In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 4516–20. New Orleans, LA: IEEE, 2017. https://doi.org/10.1109/ICASSP.2017.7953011.
[2] Dutt, A., and V. Rokhlin. “Fast Fourier Transforms for Nonequispaced Data.” SIAM Journal on Scientific Computing 14, no. 6 (November 1993): 1368–93. https://doi.org/10.1137/0914081.
Extended Capabilities
Version History
Introduced in R2020a