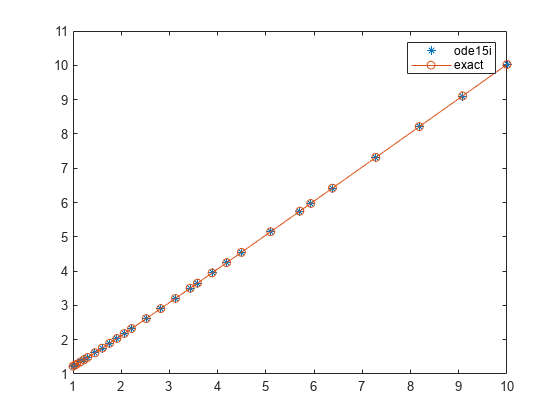
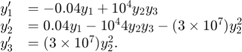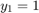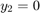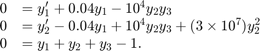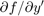ode15i
Solve fully implicit differential equations — variable order method
Syntax
Description
[ also
uses the integration settings defined by t,y] =
ode15i(odefun,tspan,y0,yp0,options)options,
which is an argument created using the odeset function.
For example, use the AbsTol and RelTol options
to specify absolute and relative error tolerances, or the Jacobian option
to provide the Jacobian matrix.
[ additionally
finds where functions of t,y,te,ye,ie]
= ode15i(odefun,tspan,y0,yp0,options)(t,y,y'), called event
functions, are zero. In the output, te is the time
of the event, ye is the solution at the time of
the event, and ie is the index of the triggered
event.
For each event function, specify whether the integration is
to terminate at a zero and whether the direction of the zero crossing
matters. Do this by setting the 'Events' property
to a function, such as myEventFcn or @myEventFcn,
and creating a corresponding function: [value,isterminal,direction]
= myEventFcn(t,y,yp).
For more information, see ODE Event Location.
sol = ode15i(___)deval to evaluate
the solution at any point on the interval [t0 tf].
You can use any of the input argument combinations in previous syntaxes.
Examples
Input Arguments
Output Arguments
Tips
Providing the Jacobian matrix to
ode15iis critical for reliability and efficiency. Alternatively, if the system is large and sparse, then providing the Jacobian sparsity pattern also assists the solver. In either case, useodesetto pass in the matrices using theJacobianorJPatternoptions.
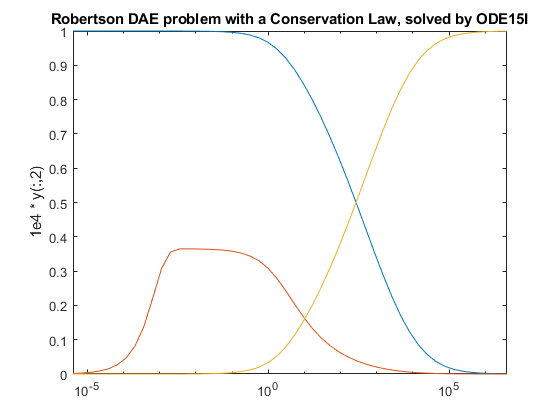
Algorithms
ode15i is a variable-step, variable-order
(VSVO) solver based on the backward differentiation formulas (BDFs)
of orders 1 to 5. ode15i is designed to be used
with fully implicit differential equations and index-1 differential
algebraic equations (DAEs). The helper function decic computes
consistent initial conditions that are suitable to be used with ode15i [1].
References
[1] Lawrence F. Shampine, “Solving 0 = F(t, y(t), y′(t)) in MATLAB,” Journal of Numerical Mathematics, Vol.10, No.4, 2002, pp. 291-310.
Version History
Introduced before R2006a