Control Quadruple-Tank Using Passivity-Based Nonlinear MPC
This example shows how to design a passivity-based controller for a quadruple-tank using nonlinear model predictive control (MPC).
Overview
The dynamics for a quadruple tank system can be written as in [1]:
,
where denotes the heights of the four tanks and denotes the flows of the two pumps. These dynamics are implemented in stateFcnQuadrupleTank.m.
The control objective is to select the flow of the pumps such that moves towards the equilibrium .
To enforce closed-loop stability, the controller includes a passivity constraint.
To define the passivity constraint, first define the state error vector:
.
As in [1], define the storage function as and take the derivative of to obtain the relationship:
.
This relationship means that, the system is passive from to . The relationship for the passivity input and the passivity output are described in the helper function getPassivityInputQuadrupleTank.m and getPassivityOutputQuadrupleTank.m.
To enforce closed-loop stability, define the passivity constraint as follows:
with .
For a nonlinear MPC controller, you define the passivity constraint by setting the Passivity property of the nonlinear MPC object.
Design Nonlinear MPC Controller
Create a nonlinear MPC object with four states, four outputs, and two inputs.
nlobj = nlmpc(4,4,2);
Zero weights are applied to one or more OVs because there are fewer MVs than OVs.
Specify the quadruple-tank dynamics function as the state function of the prediction model.
nlobj.Model.StateFcn = "stateFcnQuadrupleTank";The default cost function of a nonlinear MPC problem is a standard quadratic cost function. For this example, keep a quadratic cost function and specify nonzero weights for the first two output variables [1].
nlobj.Weights.OutputVariables = [0.1 0.1 0 0];
Specify the passivity property fields of the nonlinear MPC object.
nlobj.Passivity.EnforceConstraint = true; nlobj.Passivity.InputFcn = "getPassivityInputQuadrupleTank"; nlobj.Passivity.OutputFcn = "getPassivityOutputQuadrupleTank"; nlobj.Passivity.OutputPassivityIndex = 1;
Closed-Loop Simulation
Specify the initial conditions of the states.
x0 = [25;16;20;21];
Specify the equilibrium point for the quadruple-tank model.
xs = [28.1459,17.8230,18.3991,25.1192]'; us = [37,38]';
Open the Simulink® model.
mdl = "quadrupleTankNLMPC";
open_system(mdl)
Run the model.
sim(mdl);


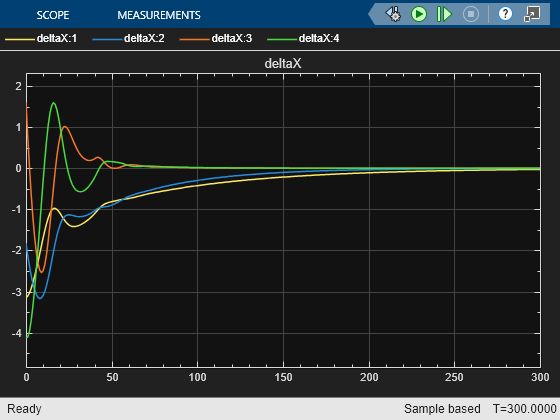
View the errors for the quadruple-tank states.
open_system(mdl + "/Quadruple-tank/state_error")
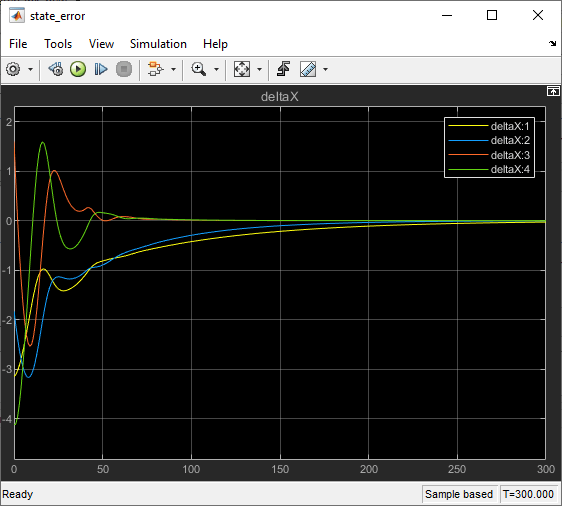
The errors go to zero and the closed-loop system is stable.
To view the performance of the nonlinear MPC controller without the passivity constraint, remove it from the controller.
nlobj.Passivity.EnforceConstraint = false;
Run the simulation.
sim(mdl);
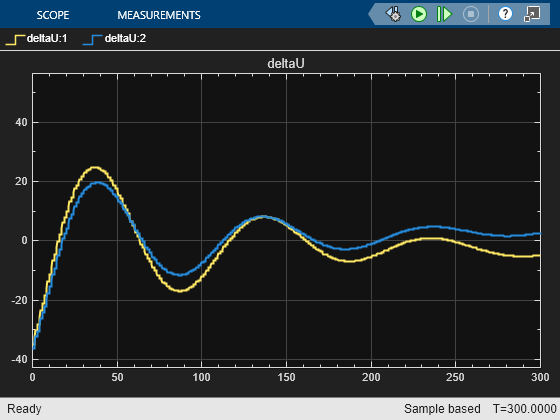

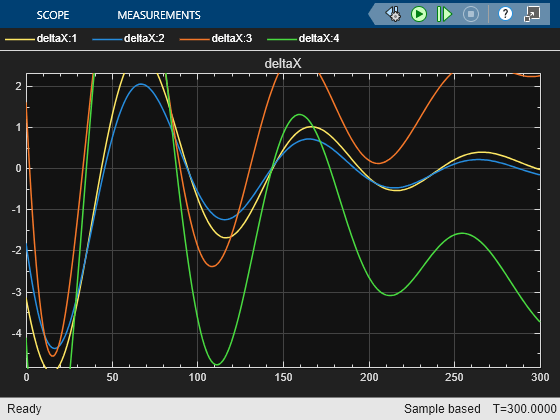

Without the passivity constraint, the closed-loop system becomes unstable with the same controller design parameters.
References
[1] Raff, Tobias, Christian Ebenbauer, and Frank Allgöwer. “Nonlinear Model Predictive Control: A Passivity-Based Approach.” In Assessment and Future Directions of Nonlinear Model Predictive Control, edited by Rolf Findeisen, Frank Allgöwer, and Lorenz T. Biegler, 358:151–62. Berlin, Heidelberg: Springer Berlin Heidelberg, 2007. https://doi.org/10.1007/978-3-540-72699-9_12.