Gain-Scheduled Implicit and Explicit MPC Control of Mass-Spring System
This example shows how to use a Multiple MPC Controllers block and a Multiple Explicit MPC Controllers block to implement a gain scheduled MPC control of a nonlinear plant.
System Description
The system is composed by two potentially colliding masses M1 and M2 connected to two springs k1 and k2 respectively. The collision is assumed completely inelastic. Mass M1 is pulled by a force F, which is the manipulated variable. The objective is to make mass M1's position y1 track a given reference r.
The dynamics are twofold: when the masses are detached, M1 moves freely. Otherwise, M1 and M2 move together. We assume that only M1 position and a contact sensor are available for feedback. The latter is used to trigger the switching of the MPC controllers. Note that the position and velocity of mass M2 are not directly controllable. Units are in MKS unless otherwise specified.
/-----\ k1 ||
F <--- | M1 |----/\/\/\-------------[|| wall
|| | |---/ ||
|| k2 \-/ /----\ ||
wall||]--/\/\/\-------------------| M2 | ||
|| \----/ ||
|| ||
----yeq2------------------ y1 ------ y2 ----------------yeq1----> y axisThe model is a simplified version of the model proposed in [1].
Model Parameters
M1 = 1; % mass #1 M2 = 5; % mass #2 k1 = 1; % spring #1 constant k2 = 0.1; % spring #2 onstant b1 = 0.3; % friction coefficient for spring #1 b2 = 0.8; % friction coefficient for spring #2 yeq1 = 10; % wall mount position for spring #1 yeq2 = -10; % wall mount position for spring #2
Plant Models
The state-space plant models for this examples have the following input and output signals:
States: Position and velocity of mass
M1Manipulated variable: Pulling force
FMeasured disturbance: Constant value of
1which calibrates the spring force to the correct valueMeasured output: Position of mass
M1
Define the state-space model of M1 when the masses are not in contact.
A1 = [0 1;-k1/M1 -b1/M1];
B1 = [0 0;-1/M1 k1*yeq1/M1];
C1 = [1 0];
D1 = [0 0];
sys1 = ss(A1,B1,C1,D1);
sys1 = setmpcsignals(sys1,'MD',2);
-->Assuming unspecified input signals are manipulated variables.
Define the state-space model when the two masses are in contact.
A2 = [0 1;-(k1+k2)/(M1+M2) -(b1+b2)/(M1+M2)];
B2 = [0 0;-1/(M1+M2) (k1*yeq1+k2*yeq2)/(M1+M2)];
C2 = [1 0];
D2 = [0 0];
sys2 = ss(A2,B2,C2,D2);
sys2 = setmpcsignals(sys2,'MD',2);
-->Assuming unspecified input signals are manipulated variables.
Design MPC Controllers
Specify the controllers sample time Ts, prediction horizon p, and control horizon m.
Ts = 0.2; p = 20; m = 1;
Design the first MPC controller, for the case when mass M1 is detached from M2.
MPC1 = mpc(sys1,Ts,p,m); MPC1.Weights.OV = 1;
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
Specify constraints on the manipulated variable.
MPC1.MV = struct('Min',0,'Max',30,'RateMin',-10,'RateMax',10);
Design the second MPC controller for the case when masses M1 and M2 are together.
MPC2 = mpc(sys2,Ts,p,m); MPC2.Weights.OV = 1;
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
Specify constraints on the manipulated variable.
MPC2.MV = struct('Min',0,'Max',30,'RateMin',-10,'RateMax',10);
Simulate Gain Scheduled MPC in Simulink
Simulate gain-scheduled MPC control using the Multiple MPC Controllers block, which switches between MPC1 and MPC2. Open and configure the model.
y1initial = 0; % Initial position of M1 y2initial = 10; % Initial position of M2 mdl = 'mpc_switching'; open_system(mdl)
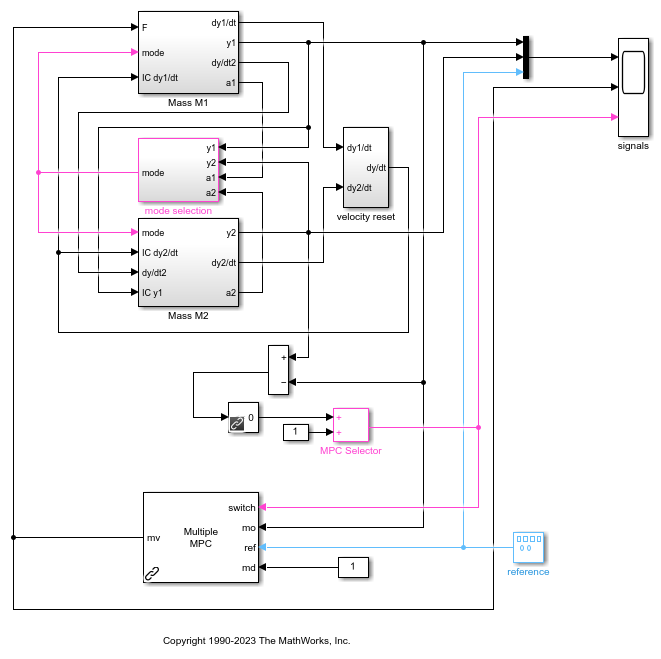
The mode selection block outputs a mode signal which selects the right system dynamics (mass M2 either disengaged or engaged) depending on the relative position and acceleration of both masses. The Multiple MPC controller block uses the MPC Selector signal, which depends on the relative mass position, to switch between the two controllers given as parameters.
Simulate the model.
open_system([mdl '/signals'])
sim(mdl)
MPC1saved = MPC1;
MPC2saved = MPC2;
-->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output. -->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output. -->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output.
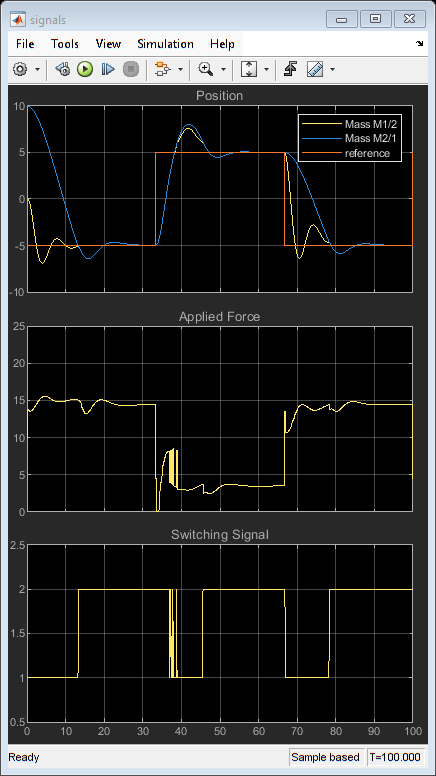
Using two controllers provides satisfactory performance under all conditions.
Repeat Simulation Using MPC1 Only
Repeat the simulation assuming that the masses are never in contact; that is, using only controller MPC1.
MPC1 = MPC1saved; MPC2 = MPC1saved; sim(mdl)
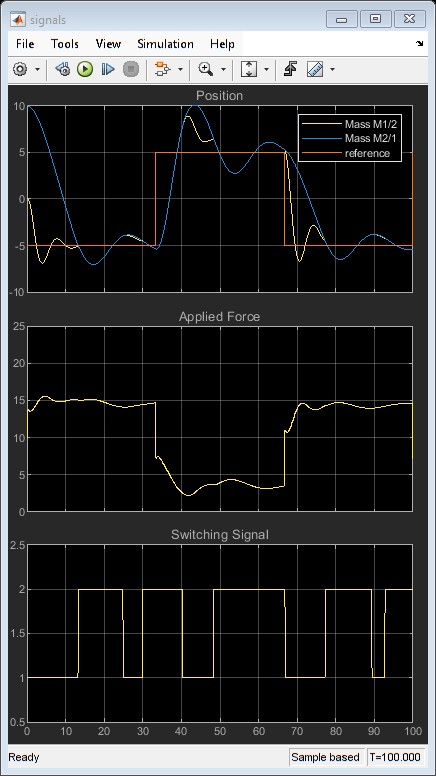
In this case, performance degrades whenever the two masses join.
Repeat Simulation Using MPC2 Only
Repeat the simulation assuming that the masses are always in contact; that is, using only controller MPC2.
MPC1 = MPC2saved; MPC2 = MPC2saved; sim(mdl)
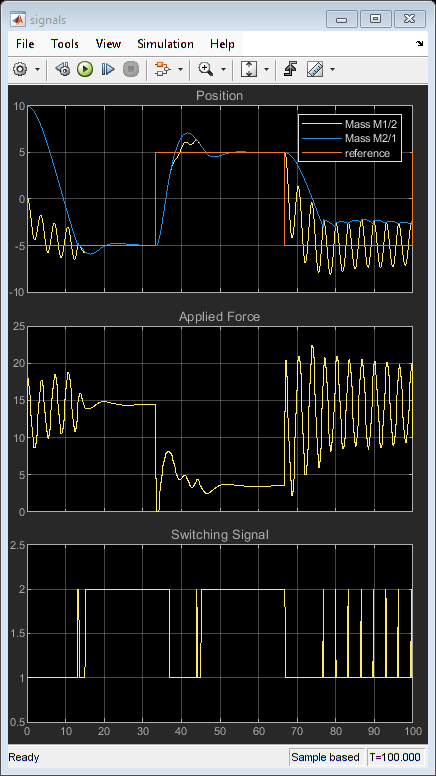
In this case, performance degrades when the masses separate, causing the controller to apply excessive force.
bdclose(mdl);
Design Explicit MPC Controllers
To reduce online computational effort, you can create an explicit MPC controller for each operating condition, and implement gain-scheduled explicit MPC control using the Multiple Explicit MPC Controllers block. To create an explicit MPC controller, first define the operating ranges for the controller states, input signals, and reference signals.
To get the controller input and output disturbance models, use getindist and getoutdist, respectively. There is no input disturbance model, while the output disturbance model has one state.
size(getindist(MPC1saved)) size(getoutdist(MPC1saved))
State-space model with 0 outputs, 0 inputs, and 0 states. State-space model with 1 outputs, 1 inputs, and 1 states.
To display the controller initial states, use mpcstate.
mpcstate(MPC1saved)
MPCSTATE object with fields
Plant: [0 0]
Disturbance: 0
Noise: [1×0 double]
LastMove: 0
Covariance: [3×3 double]
Create an explicit MPC range object using the corresponding traditional controller, MPC1.
range = generateExplicitRange(MPC1saved);
Specify the ranges for the controller states. Both MPC1 and MPC2 contain states for:
The position and velocity of mass
M1The integrator from the default output disturbance model
range.State.Min(:) = [-10;-8;-3]; range.State.Max(:) = [10;8;3];
When possible, use your knowledge of the plant to define the state ranges. Setting the range of a state variable is sometimes difficult when the state does not correspond to a physical parameter. In that case, multiple runs of open-loop plant simulation with typical reference and disturbance signals, including model mismatches, are recommended to collect data that reflect the ranges of the states.
Note that if at run time one of these independent variables falls outside of its range, the controller returns an error status and sets the manipulated variables to their last values. Therefore, it is important that you do not underestimate these ranges.
For this system, you can activate the optional est.state outport of the Multiple MPC Controllers block, and view the estimated states using a scope. When simulating the controller responses, use a reference signal that covers the expected operating range.
Define the range for the reference signal. Select a reference range that is smaller than the M1 position range.
range.Reference.Min = -8; range.Reference.Max = 8;
Specify the manipulated variable range using the defined MV constraints.
range.ManipulatedVariable.Min = 0; range.ManipulatedVariable.Max = 30;
Define the range for the measured disturbance signal. Since the measured disturbance is constant, specify a small range around the constant value, 1.
range.MeasuredDisturbance.Min = 0.9; range.MeasuredDisturbance.Max = 1.1;
Create an explicit MPC controller that corresponds to MPC1 using the specified range object.
expMPC1 = generateExplicitMPC(MPC1saved,range);
Regions found / unexplored: 4/ 0
Create an explicit MPC controller that corresponds to MPC2. Since MPC1 and MPC2 operate over the same state and input ranges, and have the same constraints, you can use the same range object.
expMPC2 = generateExplicitMPC(MPC2saved,range);
Regions found / unexplored: 5/ 0
In general, the explicit MPC ranges of different controllers may not match. For example, the controllers may have different constraints or state ranges. In such cases, create a separate explicit MPC range object for each controller.
Validate Explicit MPC Controllers
It is good practice to validate the performance of each explicit MPC controller before implementing gain-scheduled explicit MPC. For example, to compare the performance of MPC1 and expMPC1, simulate the closed-loop response of each controller using sim.
r = [zeros(30,1); 5*ones(160,1); -5*ones(160,1)]; [Yimp,Timp,Uimp] = sim(MPC1saved,350,r,1); [Yexp,Texp,Uexp] = sim(expMPC1,350,r,1);
-->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output.
Compare the plant output and manipulated variable sequences for the two controllers.
figure subplot(2,1,1) plot(Timp,Yimp,'b-',Texp,Yexp,'r--') grid on xlabel('Time (s)') ylabel('Output') title('Explicit MPC Validation') legend('Implicit MPC','Explicit MPC') subplot(2,1,2) plot(Timp,Uimp,'b-',Texp,Uexp,'r--') grid on ylabel('MV') xlabel('Time (s)')
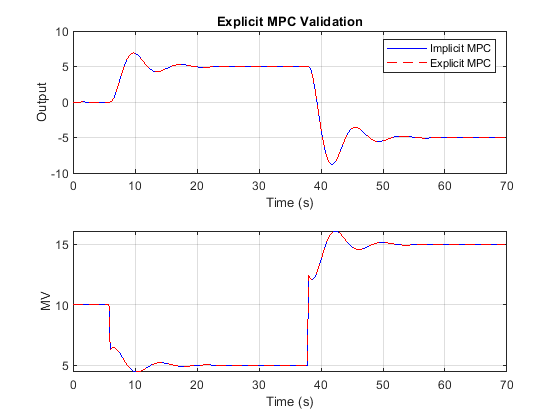
The closed-loop responses and manipulated variable sequences of the implicit and explicit controllers match. Similarly, you can validate the performance of expMPC2 against that of MPC2.
If the responses of the implicit and explicit controllers do not match, adjust the explicit MPC ranges, and create a new explicit MPC controller.
Simulate Gain-Scheduled Explicit MPC
To implement gain-scheduled explicit MPC control, replace the Multiple MPC Controllers block with the Multiple Explicit MPC Controllers block.
expModel = 'mpc_switching_explicit';
open_system(expModel)
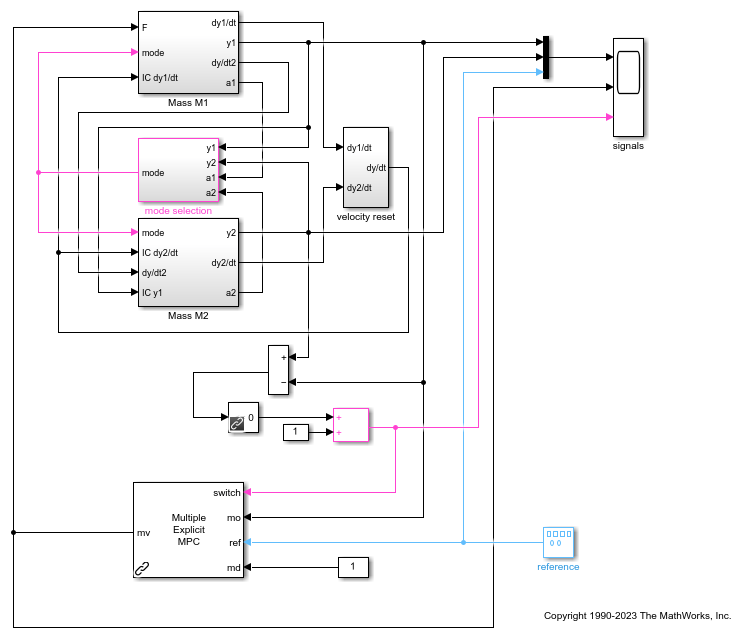
To view the simulation results, open the signals scope.
open_system([expModel '/signals']) % Run the simulation. sim(expModel)
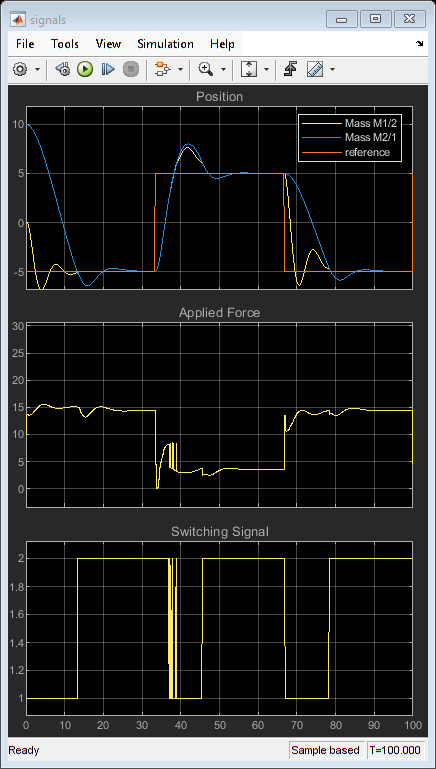
The gain-scheduled explicit MPC controllers provide the same performance as the gain-scheduled implicit MPC controllers.
References
[1] A. Bemporad, S. Di Cairano, I. V. Kolmanovsky, and D. Hrovat, "Hybrid modeling and control of a multibody magnetic actuator for automotive applications," in Proc. 46th IEEE® Conf. on Decision and Control, New Orleans, LA, 2007.
bdclose(expModel)
See Also
Functions
Objects
mpc|mpcstate|mpcmoveopt