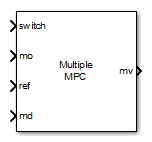
Multiple MPC Controllers
Simulate switching between multiple implicit MPC controllers
Libraries:
Model Predictive Control Toolbox
Description
At each control instant the Multiple MPC Controllers block receives the current measured plant output, reference, and measured plant disturbance (if any). In addition, it receives a switching signal that selects the active controller from a list of candidate MPC controllers designed at different operating points within the operating range. The active controller then solves a quadratic program to determine the optimal plant manipulated variables for the current input signals.
The Multiple MPC Controllers block enables you to achieve better control
when operating conditions change. Using available measurements, you can detect the current
operating region at run time and choose the appropriate active controller via the
switch input port. Switching controllers for different operating regions
is a common approach to solving nonlinear control problems using linear control
techniques.
To improve efficiency, inactive controllers do not compute optimal control moves. However, to provide bumpless transfer between controllers, the inactive controllers continue to perform state estimation.
The Multiple MPC Controllers block lacks several optional features found in the MPC Controller block, as follows:
You cannot disable optimization. One controller must always be active.
You cannot initiate a controller design from within the block dialog box; that is, there is no Design button. Design all candidate controllers before configuring the Multiple MPC Controllers block.
Similarly, there is no Review button. Instead, use the
reviewcommand or the MPC Designer app.You cannot update custom constraints on linear combinations of inputs and outputs at run time.
Both the Multiple MPC Controllers block and the Adaptive MPC Controller block enable your control system to adapt to changing operating conditions at run time. The following table lists the advantages of using each block.
| Block | Adaptive MPC Controller | Multiple MPC Controllers |
|---|---|---|
| Adaptation approach | Update prediction model for a single controller as operating conditions change | Switch between multiple controllers designed for different operating regions |
| Advantages |
|
|
Examples
Gain-Scheduled Implicit and Explicit MPC Control of Mass-Spring System
Implement gain-scheduled MPC control of a nonlinear plant using the Multiple MPC Controllers block and Multiple Explicit MPC Controllers block.
Gain-Scheduled MPC Control of Nonlinear Chemical Reactor
Control a nonlinear chemical reactor using a gain-scheduled model predictive controller as the reactor transitions from one operating condition to another.
Ports
Input
Required Inputs
Plant output reference values, specified as a row vector signal or matrix signal.
To use the same reference values across the prediction horizon, connect ref to a row vector signal with Ny elements, where Ny is the number of output variables. Each element specifies the reference for an output variable.
To vary the references over the prediction horizon (previewing) from time k+1 to time k+p, connect ref to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the references for one prediction horizon step. If you specify fewer than p rows, the final references are used for the remaining steps of the prediction horizon.
Use the switch input port to select the active controller. The switch input signal must be a scalar integer from 1 to Nc, where Nc is the number of specified candidate controllers. At each control instant, this signal designates the active controller. A switch value of 1 corresponds to the first entry in the cell array of candidate controllers, a value of 2 corresponds to the second controller, and so on.
If the switch signal is outside of the range 1 to Nc, the block retains the previous controller output.
Measured output signals, specified as a vector signal. The candidate controllers use the measured plant outputs to improve their state estimates.
All candidate controllers must use the same state estimation option, either default or custom. If your candidate controllers use default state estimation, you must connect the measured plant outputs to the mo input port. If your candidate controllers use custom state estimation, you must connect the estimated plant state signal to the x[k|k] input port.
Dependencies
To enable this port, clear the Use custom state estimation instead of using the built-in Kalman filter parameter.
Custom state estimate, specified as a vector signal. The candidate controllers use the connected state estimates instead of estimating the states using the built-in estimator. Use custom state estimates when an alternative estimation technique is considered superior to the built-in estimator or when the states are fully measurable.
All candidate controllers must use the same state estimation option, either default or custom. If your candidate controllers use custom state estimation, you must connect current state estimates to the x[k|k] input port. If your candidate controllers use default state estimation, you must connect the measured outputs to the mo input port.
When you use custom state estimation, all candidate controllers must have the same dimensions. All candidate controllers must use the same state definitions (number and order of states) for their respective plant, disturbance, and measurement noise models.
Dependencies
To enable this port, select the Use custom state estimation instead of using the built-in Kalman filter parameter.
Additional Inputs
If your controller prediction model has measured disturbances you must enable this port and connect to it a row vector or matrix signal.
To use the same measured disturbance values across the prediction horizon, connect md to a row vector signal with Nmd elements, where Nmd is the number of manipulated variables. Each element specifies the value for a measured disturbance.
To vary the disturbances over the prediction horizon (previewing) from time k to time k+p, connect md to a matrix signal with Nmd columns and up to p+1 rows. Here, k is the current time and p is the prediction horizon. Each row contains the disturbances for one prediction horizon step. If you specify fewer than p+1 rows, the final disturbances are used for the remaining steps of the prediction horizon.
Dependencies
To enable this port, select the Measured disturbances parameter.
Control signals used in the plant at the previous control interval, specified as a vector signal of length Nmv, where Nmv is the number of manipulated variables. All candidate controllers use this signal to update their controller state estimates at each control interval. This helps minimize bumpless transfer when the driving controller is switched. Using this input also improves state estimation accuracy when the manipulated variables (MV) vector used in the plant differs from the MV vector calculated by the block, for example, due to signal saturation or an override condition.
Controller state estimation assumes that the MV vector is piecewise constant. Therefore, at time tk, the ext.mv value must be the effective MV vector between times tk–1 and tk. For example, if the MVs are actually varying over this interval, you might supply the time-averaged value evaluated at time tk.
Note
Connect ext.mv to the MV signals actually applied to the plant in the previous control interval. Typically, these MV signals are the values generated by the driving controller block, though this is not always the case. If the controller block is not driving the plant, then feeding the actual control signal to ext.mv can also help achieve bumpless transfer when the controller is switched back online.
Using this option when the controller is driving the plant can cause an algebraic loop in the Simulink® model, since there is direct feedthrough from the ext.mv input to the mv outport. To prevent such algebraic loops, insert a Memory block or Unit Delay block.
For an example that uses the external manipulated variable input port for bumpless transfer, see Switch Controller Online and Offline with Bumpless Transfer.
Dependencies
To enable this port, select the External manipulated variable parameter.
Online Constraints
To specify run-time minimum output variable constraints, enable this input port. If
this port is disabled, the block uses the lower bounds specified in the
OutputVariables.Min property of its mpc controller object. If an output variable has no lower bound specified
in the controller object, then at run time the block ignores the corresponding connected
signal.
To change the bounds over the prediction horizon from time k+1 to time k+p, connect ymin to a matrix signal with Ny columns and up to p rows. Here, Ny is the number of plant outputs, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one output variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the ymin signal corresponds
to the ith plant output, and replaces the
OutputVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar OutputVariables(i).Min in the mpc
object (a constant bound for the ith plant output to be applied
to all prediction steps)
| ymin Dimension | Replacement Behavior |
|---|---|
| Scalar ymin (single output, constant bound) | ymin replaces the constant bound defined in
OutputVariables(i).Min. |
| Column vector ymin (single output, time-varying bound) | ymin replaces the constant bound defined in
OutputVariables(i).Min with a time-varying
bound. |
| Row vector ymin (multiple outputs, constant bounds) | The ith element of ymin
replaces the constant bound defined in
OutputVariables(i).Min. |
| Matrix ymin (multiple outputs, time-varying bounds) | The ith column of ymin
replaces the constant bound defined in
OutputVariables(i).Min with a time-varying
bound. |
Vector OutputVariables(i).Min in the mpc
object (a time-varying bound for the ith plant output with
different values at different prediction steps)
| ymin Dimension | Replacement Behavior |
|---|---|
| Scalar ymin (single output, constant bound) | ymin replaces the first finite entry
in OutputVariables.Min and the remaining entries
in OutputVariables.Min shift up or down with the same
amount of displacement to retain the profile defined by the original
OutputVariables.Min vector. |
| Column vector ymin (single output, time-varying bound) | ymin replaces the time-varying bound defined in
OutputVariables(i).Min, and the original bound
profile is discarded. |
| Row vector ymin (multiple outputs, constant bounds) | The ith element of ymin
replaces the first finite entry
in OutputVariables(i).Min and the remaining
entries in OutputVariables(i).Min shift up or down
with the same amount of displacement to retain the profile defined by
the original OutputVariables(i).Min vector. |
| Matrix ymin (multiple outputs, time-varying bounds). | The ith column of ymin
replaces the time-varying bound defined in
OutputVariables(i).Min, and the original bound
profile is discarded. |
Dependencies
To enable this port, select the Lower OV limits parameter.
To specify run-time maximum output variable constraints, enable this input port. If
this port is disabled, the block uses the upper bounds specified in the
OutputVariables.Max property of its mpc controller object. If an output variable has no upper bound specified
in the controller object, then at run time the block ignores the corresponding connected
signal.
To change the bounds over the prediction horizon from time k+1 to time k+p, connect ymax to a matrix signal with Ny columns and up to p rows. Here, Ny is the number of plant outputs, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one output variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the ymax signal corresponds
to the ith plant output, and replaces the
OutputVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar OutputVariables(i).Max in the mpc
object (a constant bound for the ith plant output to be applied
to all prediction steps)
| ymax Dimension | Replacement Behavior |
|---|---|
| Scalar ymax (single output, constant bound) | ymax replaces the constant bound defined in
OutputVariables(i).Max. |
| Column vector ymax (single output, time-varying bound) | ymax replaces the constant bound defined in
OutputVariables(i).Max with a time-varying
bound. |
| Row vector ymax (multiple outputs, constant bounds) | The ith element of ymax
replaces the constant bound defined in
OutputVariables(i).Max. |
| Matrix ymax (multiple outputs, time-varying bounds) | The ith column of ymax
replaces the constant bound defined in
OutputVariables(i).Max with a time-varying
bound. |
Vector OutputVariables(i).Max in the mpc
object (a time-varying bound for the ith plant output with
different values at different prediction steps)
| ymax Dimension | Replacement Behavior |
|---|---|
| Scalar ymax (single output, constant bound) | ymax replaces the first finite entry
in OutputVariables.Max and the remaining entries
in OutputVariables.Max shift up or down with the same
amount of displacement to retain the profile defined by the original
OutputVariables.Max vector. |
| Column vector ymax (single output, time-varying bound) | ymax replaces the time-varying bound defined in
OutputVariables(i).Max, and the original bound
profile is discarded. |
| Row vector ymax (multiple outputs, constant bounds) | The ith element of ymax
replaces the first finite entry
in OutputVariables(i).Max and the remaining
entries in OutputVariables(i).Max shift up or down
with the same amount of displacement to retain the profile defined by
the original OutputVariables(i).Max vector. |
| Matrix ymax (multiple outputs, time-varying bounds). | The ith column of ymax
replaces the time-varying bound defined in
OutputVariables(i).Max, and the original bound
profile is discarded. |
Dependencies
To enable this port, select the Upper OV limits parameter.
To specify run-time minimum manipulated variable constraints, enable this input port.
If this port is disabled, the block uses the lower bounds specified in the
ManipulatedVariables.Min property of its mpc controller object. If a manipulated variable has no lower bound
specified in the controller object, then at run time the block ignores the corresponding
connected signal.
To change the bounds over the prediction horizon from time k to time k+p-1, connect umin to a matrix signal with Nmv columns and up to p rows. Here, Nmv is the number of manipulated variables, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one manipulated variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the umin signal corresponds
to the ith manipulated variable, and replaces the
ManipulatedVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar ManipulatedVariables(i).Min in the mpc
object (a constant bound for the ith manipulated variable to be
applied to all prediction steps)
| umin Dimension | Replacement Behavior |
|---|---|
| Scalar umin (single output, constant bound) | umin replaces the constant bound defined in
ManipulatedVariables(i).Min. |
| Column vector umin (single output, time-varying bound) | umin replaces the constant bound defined in
ManipulatedVariables(i).Min with a time-varying
bound. |
| Row vector umin (multiple outputs, constant bounds) | The ith element of umin
replaces the constant bound defined in
ManipulatedVariables(i).Min. |
| Matrix umin (multiple outputs, time-varying bounds) | The ith column of umin
replaces the constant bound defined in
ManipulatedVariables(i).Min with a time-varying
bound. |
Vector ManipulatedVariables(i).Min in the mpc
object (a time-varying bound for the ith manipulated variable
with different values at different prediction steps)
| umin Dimension | Replacement Behavior |
|---|---|
| Scalar umin (single output, constant bound) | umin replaces the first finite entry
in ManipulatedVariables.Min and the remaining
entries in ManipulatedVariables.Min shift up or down
with the same amount of displacement to retain the profile defined by
the original ManipulatedVariables.Min vector. |
| Column vector umin (single output, time-varying bound) | umin replaces the time-varying bound defined in
ManipulatedVariables(i).Min, and the original
bound profile is discarded. |
| Row vector umin (multiple outputs, constant bounds) | The ith component of umin
replaces the first finite entry
in ManipulatedVariables(i).Min and the remaining
entries in ManipulatedVariables(i).Min shift up or
down with the same amount of displacement to retain the profile defined
by the original ManipulatedVariables(i).Min
vector. |
| Matrix umin (multiple outputs, time-varying bounds). | The ith column of umin
replaces the time-varying bound defined in
ManipulatedVariables(i).Min, and the original
bound profile is discarded. |
Dependencies
To enable this port, select the Lower MV limits parameter.
To specify run-time maximum manipulated variable constraints, enable this input port.
If this port is disabled, the block uses the upper bounds specified in the
ManipulatedVariables.Max property of its mpc controller object. If a manipulated variable has no upper bound
specified in the controller object, then at run time the block ignores the corresponding
connected signal.
To change the bounds over the prediction horizon from time k to time k+p-1, connect umax to a matrix signal with Nmv columns and up to p rows. Here, Nmv is the number of manipulated variables, k is the current time, and p is the prediction horizon. Each row contains the bounds for one prediction horizon step. If you specify fewer than p rows, the bounds in the final row apply for the remainder of the prediction horizon. If there is only one manipulated variable, and a vector signal with no more than p entries is connected, then these entries are used across the prediction horizon.
The ith column of the umax signal corresponds
to the ith manipulated variable, and replaces the
ManipulatedVariables(i).Max property of the mpc object at run time. The replacement behavior depends on the dimensions
of both variables.
Scalar ManipulatedVariables(i).Max in the mpc
object (a constant bound for the ith manipulated variable to be
applied to all prediction steps)
| umax Dimension | Replacement Behavior |
|---|---|
| Scalar umax (single output, constant bound) | umax replaces the constant bound defined in
ManipulatedVariables(i).Max. |
| Column vector umax (single output, time-varying bound) | umax replaces the constant bound defined in
ManipulatedVariables(i).Max with a time-varying
bound. |
| Row vector umax (multiple outputs, constant bounds) | The ith element of umax
replaces the constant bound defined in
ManipulatedVariables(i).Max. |
| Matrix umax (multiple outputs, time-varying bounds) | The ith column of umax
replaces the constant bound defined in
ManipulatedVariables(i).Max with a time-varying
bound. |
Vector ManipulatedVariables(i).Max in the mpc
object (a time-varying bound for the ith manipulated variable
with different values at different prediction steps)
| umax Dimension | Replacement Behavior |
|---|---|
| Scalar umax (single output, constant bound) | umax replaces the first finite entry
in ManipulatedVariables.Max and the remaining
entries in ManipulatedVariables.Max shift up or down
with the same amount of displacement to retain the profile defined by
the original ManipulatedVariables.Max vector. |
| Column vector umax (single output, time-varying bound) | umax replaces the time-varying bound defined in
ManipulatedVariables(i).Max, and the original
bound profile is discarded. |
| Row vector umax (multiple outputs, constant bounds) | The ith element of umax
replaces the first finite entry
in ManipulatedVariables(i).Max and the remaining
entries in ManipulatedVariables(i).Max shift up or
down with the same amount of displacement to retain the profile defined
by the original ManipulatedVariables(i).Max
vector. |
| Matrix umax (multiple outputs, time-varying bounds). | The ith column of umax
replaces the time-varying bound defined in
ManipulatedVariables(i).Max, and the original
bound profile is discarded. |
Dependencies
To enable this port, select the Upper MV limits parameter.
Online Tuning Weights
To specify run-time output variable tuning weights, enable this input port. If this port is disabled, the block uses the tuning weights specified in the Weights.OutputVariables property of its controller object. These tuning weights penalize deviations from output references.
If the MPC controller object uses constant output tuning weights over the prediction horizon, you can specify only constant output tuning weights at runtime. Similarly, if the MPC controller object uses output tuning weights that vary over the prediction horizon, you can specify only time-varying output tuning weights at runtime.
To use constant tuning weights over the prediction horizon, connect y.wt to a row vector signal with Ny elements, where Ny is the number of outputs. Each element specifies a nonnegative tuning weight for an output variable. For more information on specifying tuning weights, see Tune Weights.
To vary the tuning weights over the prediction horizon from time k+1 to time k+p, connect y.wt to a matrix signal with Ny columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.
Dependencies
To enable this port, select the OV weights parameter.
To specify run-time manipulated variable tuning weights, enable this input port. If
this port is disabled, the block uses the tuning weights specified in the
Weights.ManipulatedVariables property of its controller object.
These tuning weights penalize deviations from MV targets.
If the MPC controller object uses constant manipulated variable tuning weights over the prediction horizon, you can specify only constant manipulated variable tuning weights at runtime. Similarly, if the MPC controller object uses manipulated variable tuning weights that vary over the prediction horizon, you can specify only time-varying manipulated variable tuning weights at runtime.
To use the same tuning weights over the prediction horizon, connect u.wt to a row vector signal with Nmv elements, where Nmv is the number of manipulated variables. Each element specifies a nonnegative tuning weight for a manipulated variable. For more information on specifying tuning weights, see Tune Weights.
To vary the tuning weights over the prediction horizon from time k to time k+p-1, connect u.wt to a matrix signal with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.
Dependencies
To enable this port, select the MV weights parameter.
To specify run-time manipulated variable rate tuning weights, enable this input port. If this port is disabled, the block uses the tuning weights specified in the Weights.ManipulatedVariablesRate property of its controller object. These tuning weights penalize large changes in control moves.
If the MPC controller object uses constant manipulated variable rate tuning weights over the prediction horizon, you can specify only constant manipulated variable tuning rate weights at runtime. Similarly, if the MPC controller object uses manipulated variable rate tuning weights that vary over the prediction horizon, you can specify only time-varying manipulated variable rate tuning weights at runtime.
To use the same tuning weights over the prediction horizon, connect du.wt to a row vector signal with Nmv elements, where Nmv is the number of manipulated variables. Each element specifies a nonnegative tuning weight for a manipulated variable rate. For more information on specifying tuning weights, see Tune Weights.
To vary the tuning weights over the prediction horizon from time k to time k+p-1, connect du.wt to a matrix signal with Nmv columns and up to p rows. Here, k is the current time and p is the prediction horizon. Each row contains the tuning weights for one prediction horizon step. If you specify fewer than p rows, the tuning weights in the final row apply for the remainder of the prediction horizon. For more information on varying weights over the prediction horizon, see Setting Time-Varying Weights and Constraints with MPC Designer.
Dependencies
To enable this port, select the MVRate weights parameter.
To specify a run-time slack variable tuning weight, enable this input port and connect a scalar signal. If this port is disabled, the block uses the tuning weight specified in the Weights.ECR property of its controller object.
The slack variable tuning weight has no effect unless your controller object defines soft constraints whose associated ECR values are nonzero. If there are soft constraints, increasing the ecr.wt value makes these constraints relatively harder. The controller then places a higher priority on minimizing the magnitude of the predicted worst-case constraint violation.
Dependencies
To enable this port, select the ECR weight parameter.
Output
Required Output
Optimal manipulated variable control action, output as a column vector signal of length Nmv, where Nmv is the number of manipulated variables. The Multiple MPC Controllers block passes the output of the active controller to the mv output port.
If the solver of the active controller converges to a local optimum solution (qp.status is positive), then mv contains the optimal solution.
If the solver fails (qp.status is negative), then mv remains at its most recent successful solution; that is, the controller output freezes.
If the solver reaches the maximum number of iterations without finding an optimal
solution (qp.status is zero) and the
Optimization.UseSuboptimalSolution property of the active
controller is:
true, then mv contains the suboptimal solutionfalse, then mv then mv remains at its most recent successful solution
Additional Outputs
Objective function cost, output as a nonnegative scalar signal. The cost quantifies the degree to which the controller has achieved its objectives. The cost value is calculated using the scaled MPC cost function in which every term is offset-free and dimensionless.
The cost value is only meaningful when the qp.status output is nonnegative.
Dependencies
To enable this port, select the Optimal cost parameter.
Optimization status of the active controller, output as an integer signal.
If the active controller solves the QP problem for a given control interval, the qp.status output returns the number of QP solver iterations used in computation. This value is a finite, positive integer and is proportional to the time required for the calculations. Therefore, a large value means a relatively slow block execution for this time interval.
The QP solver can fail to find an optimal solution for the following reasons:
qp.status =
0— The QP solver cannot find a solution within the maximum number of iterations specified in thempcobject. In this case, if theOptimizer.UseSuboptimalSolutionproperty of the active controller isfalse, the block holds its mv output at the most recent successful solution. Otherwise, it uses the suboptimal solution found during the last solver iteration.qp.status =
-1— The QP solver detects an infeasible QP problem. See Monitoring Optimization Status to Detect Controller Failures for an example where a large, sustained disturbance drives the output variable outside its specified bounds. In this case, the block holds its mv output at the most recent successful solution.qp.status =
-2— The QP solver has encountered numerical difficulties in solving a severely ill-conditioned QP problem. In this case, the block holds its mv output at the most recent successful solution.
In a real-time application, you can use qp.status to set an alarm or take other special action.
Dependencies
To enable this port, select the Optimization status parameter.
Estimated controller states of the active controller, output as a vector signal. The estimated states include the plant, disturbance, and noise model states.
Dependencies
To enable this port, select the Estimated controller states parameter.
Optimal Sequences
Optimal manipulated variable sequence, returned as a matrix signal with p+1 rows and Nmv columns, where p is the prediction horizon and Nmv is the number of manipulated variables.
The first p rows of mv.seq contain the calculated optimal manipulated variable values from current time k to time k+p-1. The first row of mv.seq contains the current manipulated variable values (output mv). Since the controller does not calculate optimal control moves at time k+p, the final two rows of mv.seq are identical.
Dependencies
To enable this port, select the Optimal control sequence parameter.
Optimal prediction model state sequence, returned as a matrix signal with p+1 rows and Nx columns, where p is the prediction horizon and Nx is the number of states.
The first row of x.seq contains the current estimated state values, either from the built-in state estimator or from the custom state estimation block input x[k|k]. The next p rows of x.seq contain the calculated optimal state values from time k+1 to time k+p.
Dependencies
To enable this port, select the Optimal state sequence parameter.
Optimal output variable sequence, returned as a matrix signal with p+1 rows and Ny columns, where p is the prediction horizon and Ny is the number of output variables.
The first p rows of y.seq contain the calculated optimal output values from current time k to time k+p-1. The first row of y.seq is computed based on the current estimated states and the current measured disturbances (first row of input md). Since the controller does not calculate optimal output values at time k+p, the final two rows of y.seq are identical.
Dependencies
To enable this port, select the Optimal output sequence parameter.
Parameters
Candidate controllers, specified as one of the following:
The specified array must contain at least two candidate controllers. The first entry in the cell array is the controller that corresponds to a switch input value of 1, the second corresponds to a switch input value of 2, and so on.
Programmatic Use
Block Parameter:
mpcobjs |
| Type: string, character vector, cell array of strings, cell array of character vectors |
Default:
"" |
Initial states for the candidate controllers, specified as one of the following:
Cell array of
mpcstateobjects.Cell array of strings or a cell array of character vectors, where each element is the name of an
mpcstateobject in the MATLAB workspace.{[],[],...},{'[]','[]',...}, or{"[]","[]",...}— Use the nominal condition defined inModel.Nominalproperty of each candidate controller as its initial state.
Use this parameter make the controller states reflect the true plant environment at
the start of your simulation to the best of your knowledge. This initial states can
differ from the nominal states defined in the mpc objects.
If custom state estimation is enabled, the block ignores Cell Array of Initial Controller States parameter.
Programmatic Use
Block Parameter:
x0s |
| Type: string, character vector, cell array of strings, cell array of character vectors |
Default:
"" |
General Tab
If your controller has measured disturbances, you must select this parameter to add the md output port to the block.
Programmatic Use
Block Parameter: md_inport_multiple |
| Type: string, character vector |
Values: "off", "on" |
Default: "on" |
Select this parameter to add the ext.mv input port to the block.
Programmatic Use
Block Parameter: mv_inport_multiple |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the mv.target input port to the block.
Programmatic Use
Block Parameter:
uref_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the cost output port to the block.
Programmatic Use
Block Parameter:
return_cost_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the qp.status output port to the block.
Programmatic Use
Block Parameter:
return_qpstatus_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the est.state output port to the block.
Programmatic Use
Block Parameter: return_state_multiple |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Select this parameter to add the mv.seq output port to the block.
Programmatic Use
Block Parameter:
return_mvseq_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the x.seq output port to the block.
Programmatic Use
Block Parameter:
return_xseq_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the y.seq output port to the block.
Programmatic Use
Block Parameter:
return_ovseq_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to remove the mo input port and add the x[k|k] input port.
Programmatic Use
Block Parameter: state_inport_multiple |
| Type: string, character vector |
Values: "off", "on" |
Default: "off" |
Online Features Tab
Select this parameter to add the ymin input port to the block.
Programmatic Use
Block Parameter:
ymin_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the ymax input port to the block.
Programmatic Use
Block Parameter:
ymax_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the umin input port to the block.
Programmatic Use
Block Parameter:
umin_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the umax input port to the block.
Programmatic Use
Block Parameter:
umax_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the E, F, G, and S input ports to the block.
Programmatic Use
Block Parameter:
cc_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the y.wt input port to the block.
Programmatic Use
Block Parameter:
ywt_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the u.wt input port to the block.
Programmatic Use
Block Parameter:
uwt_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the du.wt input port to the block.
Programmatic Use
Block Parameter:
duwt_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Select this parameter to add the ecr.wt input port to the block.
Programmatic Use
Block Parameter:
rhoeps_inport_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Others Tab
Specify the block data type of the manipulated variables as one of the following:
double— Double-precision floating pointsingle— Single-precision floating pointIf you are implementing the block on a single-precision target, specify the output data type as
single.data type expression— An expression that evaluates to eitherdoubleorsingle. For more information see Control Data Types of Signals (Simulink).
Programmatic Use
Block Parameter:
BlockDataType_multiple |
| Type: string, character vector |
Values:
"double", "single", data type
expression |
Default: "double" |
Select this parameter to inherit the sample time of the parent subsystem as the block sample time. Doing so allows you to conditionally execute this block inside Function-Call Subsystem (Simulink) or Triggered Subsystem (Simulink) blocks. For an example, see Using MPC Controller Block Inside Function-Call and Triggered Subsystems.
Note
You must execute Function-Call Subsystem or Triggered Subsystem blocks at the sample rate of the controller. Otherwise, you can see unexpected results for two reasons.
The first element of the MV rate vector (which is the difference between the current and the last value of the manipulated variable) is normally weighted and constrained assuming that the last MV value occurred in the past at the sample time specified in the MPC object, and when the block is executed with a different sample rate, this assumption no longer holds.
The built-in Kalman estimator uses the sample time specified in the MPC object to provide an estimation of the current state to the MPC optimization problem, so when the block is executed with a different sample time, the estimated state is no longer correct.
If you clear this parameter (default), the sample time of the block is inherited from the controller object.
To view the sample time of a block, in the Simulink model window, on the Debug tab, under Information Overlays, select either colors or Text. For more information, see View Sample Time Information (Simulink).
Programmatic Use
Block Parameter:
SampleTimeInherited_multiple |
| Type: string, character vector |
Values:
"off", "on" |
Default:
"off" |
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.
Version History
Introduced in R2008bThe signal dimensions of the mv.seq output port of the
Multiple MPC Controllers block have changed. Previously, this signal was a
p-by-Nmv matrix, where
p is the prediction horizon and
Nmv is the number of manipulated variables. Now,
mv.seq is a
(p+1)-by-Nmv matrix, where
row p+1 duplicates row p.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)