Lane Following Using Nonlinear Model Predictive Control

This example shows how to design a lane-following controller using the Nonlinear Model Predictive Controller block. In this example, you:

1. Design a nonlinear MPC controller (NLMPC) for lane following.

2. Compare the performance of NLMPC with adaptive MPC.

Introduction

A lane-following system is a control system that keeps the vehicle traveling along the center line of a highway lane, while maintaining a user-set velocity. The lane-following scenario is depicted in the following figure.

A lane-following system manipulates both the longitudinal acceleration and front steering angle of the vehicle to:

• Keep the lateral deviation 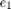and relative yaw angle 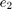small.

• Keep the longitudinal velocity close to a driver set velocity.

• Balance the above two goals when they cannot be met simultaneously.

In a separate example of lane keeping assist, it is assumed that the longitudinal velocity is constant. For more information, see Lane Keeping Assist System Using Model Predictive Control. This restriction is relaxed in this example because the longitudinal acceleration varies in this MIMO control system.

Another example augments a lane-following system with spacing control, where a safe distance from a detected lead car is also maintained. For more information, see Lane Following Control with Sensor Fusion and Lane Detection (Automated Driving Toolbox).

Overview of Simulink Model

Open the Simulink® model.

mdl = 'LaneFollowingNMPC';
open_system(mdl)

This model contains four main components:

1. Vehicle Dynamics: Apply the bicycle mode of lateral vehicle dynamics, and approximate the longitudinal dynamics using a time constant .

2. Sensor Dynamics: Approximate a sensor such as a camera to calculate the lateral deviation and relative yaw angle.

3. Lane Following Controller: Simulate nonlinear MPC and adaptive MPC.

4. Curvature Previewer: Detect the curvature at the current time step and the curvature sequence over the prediction horizon of the MPC controller.

The vehicle dynamics and sensor dynamics are discussed in more detail in Adaptive Cruise Control with Sensor Fusion (Automated Driving Toolbox). This example applies the same model for vehicle and sensor dynamics.

Parameters of Vehicle Dynamics and Road Curvature

The necessary Vehicle Dynamics and Road Curvature parameters are defined using the LaneFollowingUsingNMPCData script which is a PreLoadFcn callback of the model.

Design Nonlinear Model Predictive Controller

The continuous-time prediction model for NLMPC has the following state and output equations. The state equations are defined in LaneFollowingStateFcn.

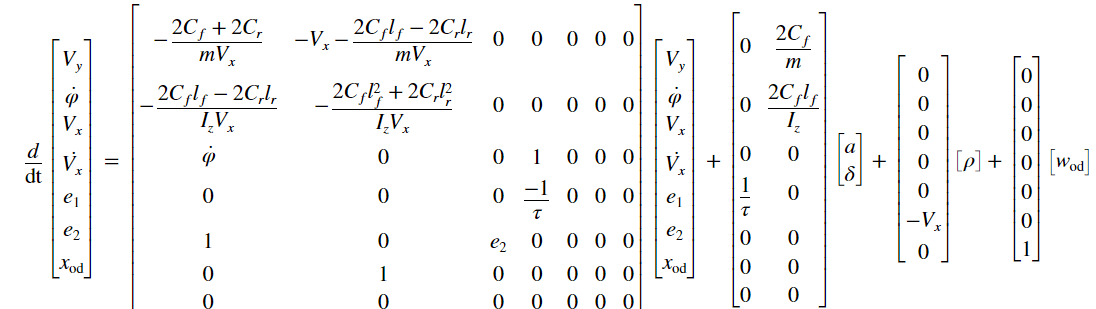
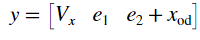
The prediction model includes an unmeasured disturbance (UD) model. The UD model describes what type of unmeasured disturbance NLMPC expects to encounter and reject in the plant. In this example, the UD model is an integrator with its input assumed to be white noise. Its output is added to the relative yaw angle. Therefore, the controller expects a random step-like unmeasured disturbance occurring at the relative yaw angle output and is prepared to reject it when it happens.

Create a nonlinear MPC controller with a prediction model that has seven states, three outputs, and two inputs. The model has two MV signals: acceleration and steering. The product of the road curvature and the longitudinal velocity is modeled as a measured disturbance, and the unmeasured disturbance is modeled by white noise.

nlobj = nlmpc(7,3,'MV',[1 2],'MD',3,'UD',4);

Zero weights are applied to one or more OVs because there are fewer MVs than OVs.

Specify the controller sample time, prediction horizon, and control horizon.

nlobj.Ts = Ts;
nlobj.PredictionHorizon = 10;
nlobj.ControlHorizon = 2;

Specify the state function for the nonlinear plant model and its Jacobian.

nlobj.Model.StateFcn = @(x,u) LaneFollowingStateFcn(x,u);
nlobj.Jacobian.StateFcn = @(x,u) LaneFollowingStateJacFcn(x,u);

Specify the output function for the nonlinear plant model and its Jacobian. The output variables are:

• Longitudinal velocity

• Lateral deviation

• Sum of the yaw angle and yaw angle output disturbance

nlobj.Model.OutputFcn = @(x,u) [x(3);x(5);x(6)+x(7)];
nlobj.Jacobian.OutputFcn = @(x,u) [0 0 1 0 0 0 0;0 0 0 0 1 0 0;0 0 0 0 0 1 1];

Set the constraints for manipulated variables.

nlobj.MV(1).Min = -3;      % Maximum acceleration 3 m/s^2
nlobj.MV(1).Max = 3;       % Minimum acceleration -3 m/s^2
nlobj.MV(2).Min = -1.13;   % Minimum steering angle -65
nlobj.MV(2).Max = 1.13;    % Maximum steering angle 65

Set the scale factors.

nlobj.OV(1).ScaleFactor = 15;   % Typical value of longitudinal velocity
nlobj.OV(2).ScaleFactor = 0.5;  % Range for lateral deviation
nlobj.OV(3).ScaleFactor = 0.5;  % Range for relative yaw angle
nlobj.MV(1).ScaleFactor = 6;    % Range of steering angle
nlobj.MV(2).ScaleFactor = 2.26; % Range of acceleration
nlobj.MD(1).ScaleFactor = 0.2;  % Range of Curvature

Specify the weights in the standard MPC cost function. The third output, yaw angle, is allowed to float because there are only two manipulated variables to make it a square system. In this example, there is no steady-state error in the yaw angle as long as the second output, lateral deviation, reaches 0 at steady state.

nlobj.Weights.OutputVariables = [1 1 0];

Penalize acceleration change more for smooth driving experience.

nlobj.Weights.ManipulatedVariablesRate = [0.3 0.1];

Validate prediction model functions at an arbitrary operating point using the validateFcns command. At this operating point:

• x0 contains the state values.

• u0 contains the input values.

• ref0 contains the output reference values.

• md0 contains the measured disturbance value.

x0 = [0.1 0.5 25 0.1 0.1 0.001 0.5];
u0 = [0.125 0.4];
ref0 = [22 0 0];
md0 = 0.1;
validateFcns(nlobj,x0,u0,md0,{},ref0);

Model.StateFcn is OK.
Jacobian.StateFcn is OK.
Model.OutputFcn is OK.
Jacobian.OutputFcn is OK.
Analysis of user-provided model, cost, and constraint functions complete.

In this example, an extended Kalman filter (EKF) provides state estimation for the seven states. The state transition function for the EKF is defined in LaneFollowingEKFStateFcn, and the measurement function is defined in LaneFollowingEKFMeasFcn.

Design Adaptive Model Predictive Controller

An adaptive MPC (AMPC) controller is also designed using the Path Following Control System block in this example. This controller uses a linear model for the vehicle dynamics and updates the model online as the longitudinal velocity varies.

In practice, as long as a linear control solution such as adaptive MPC or gain-scheduled MPC can achieve comparable control performance against nonlinear MPC, you would implement the linear control solution because it is more computationally efficient.

Compare Controller Performance

To compare the results of NLMPC and AMPC, simulate the model and save the logged data.

First, simulate the model using nonlinear MPC. To do so, set controller_type to 1.

controller_type = 1;
sim(mdl)
logsout1 = logsout;

Second, simulate the model using adaptive MPC. To do so, set controller_type to 2.

controller_type = 2;
sim(mdl)
logsout2 = logsout;

   Assuming no disturbance added to measured output #1.
   Assuming no disturbance added to measured output #2.
-->Assuming output disturbance added to measured output #3 is integrated white noise.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

Plot and compare simulation results.

LaneFollowingCompareResults(logsout1,logsout2)

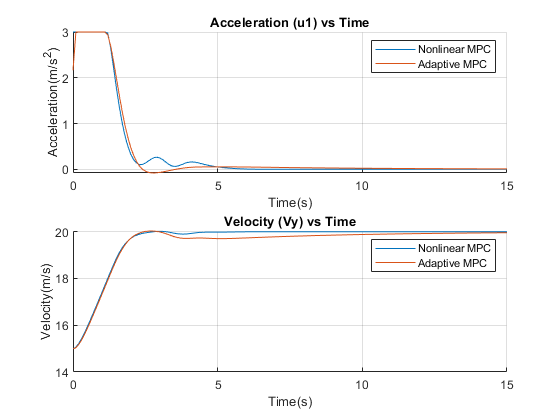
In the first plot, both nonlinear MPC and adaptive MPC give almost identical steering angle profiles. The lateral deviation and relative yaw angle are close to zero during the maneuver. This result implies that the vehicle is traveling along the desired path.

The longitudinal control command and performance for nonlinear and adaptive MPC are slightly different. The nonlinear MPC controller has smoother acceleration command and better tracking of set velocity, although the result from adaptive MPC is also acceptable.

You can also view the results via Scopes of Outputs and Inputs in the model.

Set the controller variant to nonlinear MPC.

controller_type = 1;

Conclusion

This example shows how to design a nonlinear model predictive controller for lane following. The performance of using nonlinear MPC and adaptive MPC is compared. You can select nonlinear MPC or adaptive MPC depending on the modeling information and computational power for your application.