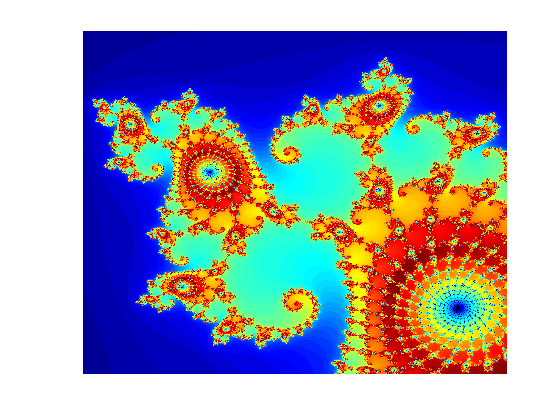
Compute the Mandelbrot Set Using GPU-Enabled Functions
This example shows how to use GPU-enabled MATLAB® functions to compute a well-known mathematical construction: the Mandelbrot set. Check your GPU using the gpuDevice function.
Define the parameters. The Mandelbrot algorithm iterates over a grid of real and imaginary parts. The following code defines the number of iterations, grid size, and grid limits.
maxIterations = 500; gridSize = 1000; xlim = [-0.748766713922161, -0.748766707771757]; ylim = [ 0.123640844894862, 0.123640851045266];
You can use the gpuArray function to transfer data to the GPU and create a gpuArray, or you can create an array directly on the GPU. gpuArray provides GPU versions of many functions that you can use to create data arrays, such as linspace. For more information, see Create GPU Arrays Directly.
x = gpuArray.linspace(xlim(1),xlim(2),gridSize); y = gpuArray.linspace(ylim(1),ylim(2),gridSize); whos x y
Name Size Bytes Class Attributes x 1x1000 8000 gpuArray y 1x1000 8000 gpuArray
Many MATLAB functions support gpuArrays. When you supply a gpuArray argument to any GPU-enabled function, the function runs automatically on the GPU. For more information, see Run MATLAB Functions on a GPU. Create a complex grid for the algorithm, and create the array count for the results. To create this array directly on the GPU, use the ones function, and specify 'gpuArray'.
[xGrid,yGrid] = meshgrid(x,y);
z0 = complex(xGrid,yGrid);
count = ones(size(z0),'gpuArray');The following code implements the Mandelbrot algorithm using GPU-enabled functions. Because the code uses gpuArrays, the calculations happen on the GPU.
z = z0; for n = 0:maxIterations z = z.*z + z0; inside = abs(z) <= 2; count = count + inside; end count = log(count);
When computations are done, plot the results.
imagesc(x,y,count)
colormap([jet();flipud(jet());0 0 0]);
axis off