Use parfor to Speed Up Monte-Carlo Code
This example shows how to speed up Monte-Carlo code by using parfor-loops. Monte-Carlo methods are found in many fields, including physics, mathematics, biology, and finance. Monte-Carlo methods involve executing a function many times with randomly distributed inputs. With Parallel Computing Toolbox™, you can replace a for-loop with a parfor-loop to easily speed up code.
This example runs a simple stochastic simulation based on the dollar auction. Run multiple simulations to find the market value for a one dollar bill using a Monte-Carlo method. In this example, the dollar auction is treated as a black-box function that produces outputs that depend on random processes. To find out more about the model, see The Dollar Auction. To see how to speed up Monte-Carlo code in general, see Use a parfor-loop to Estimate Market Value.
The Dollar Auction
The dollar auction is a non-zero-sum game first introduced by Martin Shubik in 1971. In the game, players bid for a one dollar bill. After a player makes a bid, every other player can choose to make a bid higher than the previous bidder. The auction ends when no more players decide to place a bid. The highest bidder receives the one dollar bill, however, unlike a typical auction both the highest and second-highest bidder give their bid to the auctioneer.
Stochastic Model
You can model games similar to the dollar auction using a stochastic model. The state (current bid and number of active players) can be modeled using Markov processes, and therefore outcomes (market value) can be expected to have well-defined statistics. The outcomes are drawn from a conditional distribution, and therefore the dollar auction is ideal for Monte-Carlo analysis. The market value is influenced by the following factors:
Number of players, (
nPlayers)Actions players take
In this example, the following algorithm determines what actions players take (bidding or dropping out) depending on the state.
Set the bid to the previous bid plus
incr.Select a player at random from players who are not the previous bidder.
If no bids have previously been placed, go to 8.
If the previous bid is less than 1, generate a random number between 0 and 1. If the random number is less than
dropoutRate, go to 7.Calculate how much money
gaincan be gained if the player makes a winning bid.Calculate how much money
lossthe player loses if they are the second highest bidder. Ifgainis greater thanloss, go to 8.The player drops out. Remove the player from the set of players, then go to 9.
The player places a bid.
If there are 2 or more players remaining, go to step 1.
The supporting function dollarAuction simulates a dollar auction. To view the code, see dollarAuction.m. The function takes three inputs: nPlayers, incr, and dropoutRate. Set each of the values.
nPlayers =20; incr =
0.05; dropoutRate =
0.01;
Run a random scenario by executing the dollarAuction function. Store the outputs bids and dropouts.
[bids,dropouts] = dollarAuction(nPlayers,incr,dropoutRate);
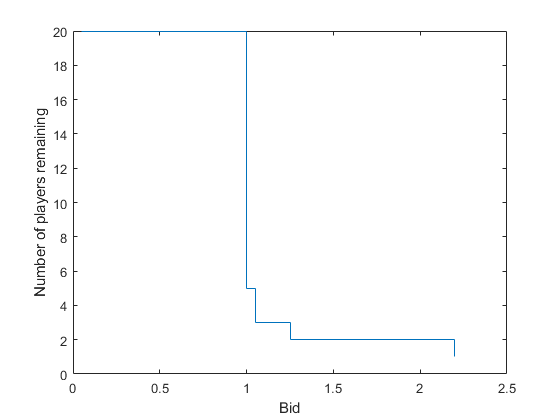
As the game continues, some players place bids and some drop out. If the bid exceeds 1, the players are locked in a "bidding war" until only one player remains.
The table dropouts contains two variables: Player, a unique number assigned to each player; Epoch, the round of bidding when Player dropped out. Use findgroups to group dropouts.Epoch, and use splitapply to get the number of players who drop out in each of the unique rounds in dropouts.Epoch.
[G,epochs] = findgroups(dropouts.Epoch); numberDropouts = splitapply(@numel,dropouts.Epoch,G);
Initially, there are no dropouts. Add this information to epochs and numberDropouts by prepending 1 and 0.
epochs = [1;epochs]; numberDropouts = [0;numberDropouts];
Use nPlayers and cumsum to calculate the number of players remaining from numberDropouts. Calculate the bids using incr and epochs. Use stairs to plot the bid against the cumulative sum of numberDropouts.
playersRemaining = nPlayers - cumsum(numberDropouts); stairs(incr*epochs,playersRemaining) xlabel('Bid') ylabel('Number of players remaining')
Estimate Market Value Using Monte-Carlo Methods
You can estimate the market value of the bill with value origValue by using Monte-Carlo methods. Here, you produce a Monte-Carlo model and compare the speed with and without Parallel Computing Toolbox. Set the number of trials nTrials used to randomly sample the outcomes.
nTrials = 10000;
You can sample the possible outcomes by executing the supporting function dollarAuction multiple times. Use a for-loop to produce nTrials samples, storing the last bid from each trial in B. Each time you run the dollarAuction function, you get different results. However, when you run the function many times, the results you produce from all of the runs will have well-defined statistics.
Record the time taken to compute nTrials simulations. To reduce statistical noise in the elapsed time, repeat this process five times, then take the minimum elapsed time.
t = zeros(1,5); for j = 1:5 tic B = zeros(1,nTrials); for i = 1:nTrials bids = dollarAuction(nPlayers,incr,dropoutRate); B(i) = bids.Bid(end); end t(j) = toc; end forTime = min(t)
forTime = 21.4323
Use histogram to plot a histogram of the final bids B. Use xline to overlay the plot with the original value (one dollar) and the average market value given by mean.
histogram(B); origLine = xline(1,'k','LineWidth',3); marketLine = xline(mean(B),'k--','LineWidth',3); xlabel('Market value') ylabel('Frequency') legend([origLine, marketLine],{'Original value','Market value'},'Location','NorthEast')

With the given algorithm and input parameters, the average market value is greater than the original value.
Use parfor-loop to Estimate Market Value
You can use Parallel Computing Toolbox to easily speed up your Monte-Carlo code. First, create a parallel pool with four workers using the 'Processes' profile.
p = parpool('Processes',4);Starting parallel pool (parpool) using the 'Processes' profile ... Connected to parallel pool with 4 workers.
Replace the for-loop with a parfor-loop. Record the time taken to compute nTrials simulations. To reduce statistical noise in the elapsed time, repeat this process 5 times then take the minimum elapsed time.
t = zeros(1,5); for j = 1:5 tic parfor i = 1:nTrials bids = dollarAuction(nPlayers,incr,dropoutRate); B(i) = bids.Bid(end); end t(j) = toc; end parforTime = min(t)
parforTime = 5.9174
With four workers, the results indicate that the code can runs over three times faster when you use a parfor-loop.
Produce Reproducible Results with Random Numbers in parfor-loops
When you generate random numbers in a parfor-loop, each run of the loop can produce different results. To create reproducible results, each iteration of the loop must have a deterministic state for the random number generator. For more information, see Repeat Random Numbers in parfor-Loops.
The supporting function dollarAuctionStream takes a fourth argument, s. This supporting function uses a specified stream to produce random numbers. To view the code, see dollarAuctionStream.m.
When you create a stream, substreams of that stream are statistically independent. For more information, see RandStream. To ensure that your code produces the same distribution of results each time, create a random number generator stream in each iteration of the loop, then set the Substream property to the loop index. Replace dollarAuction with dollarAuctionStream, then use s to run dollarAuctionStream on a worker.
Record the time taken to compute nTrials simulations. To reduce statistical noise in the elapsed time, repeat this process five times, then take the minimum elapsed time.
t = zeros(1,5); for j = 1:5 tic parfor i = 1:nTrials s = RandStream('Threefry'); s.Substream = i; bids = dollarAuctionStream(nPlayers,incr,dropoutRate,s); B(i) = bids.Bid(end); end t(j) = toc; end parforTime = min(t)
parforTime = 8.7355
Scale Up from Desktop to Cluster
You can scale your code from your desktop to a cluster with more workers. For more information about scaling up from desktop to a cluster, see Scale Up from Desktop to Cluster.
Use delete to shut down the existing parallel pool.
delete(p);
Compute the supporting function dollarAuctionStream in a parfor-loop. Run the same parfor-loop with different numbers of workers, and record the elapsed times. To reduce statistical noise in the elapsed time, run the parfor-loop five times, then take the minimum elapsed time. Record the minimum times in the array elapsedTimes. In the following code, replace MyCluster with the name of your cluster profile.
workers = [1 2 4 8 16 32]; elapsedTimes = zeros(1,numel(workers)); % Create a pool using the 'MyCluster' cluster profile p = parpool('MyCluster', 32);
Starting parallel pool (parpool) using the 'MyCluster' profile ... Connected to the parallel pool (number of workers: 32).
for k = 1:numel(workers) t = zeros(1,5); for j = 1:5 tic parfor (i = 1:nTrials, workers(k)) s = RandStream('Threefry'); s.Substream = i; bids = dollarAuctionStream(nPlayers,incr,dropoutRate,s); B(i) = bids.Bid(end); end t(j) = toc; end elapsedTimes(k) = min(t); end
Analyzing and transferring files to the workers ...done.
Calculate the computational speedup by dividing elapsedTimes(1) by the times in elapsedTimes. Examine strong scaling by plotting the speedup against the number of workers.
speedup = elapsedTimes(1) ./ elapsedTimes; plot(workers,speedup) xlabel('Number of workers') ylabel('Computational speedup')

The computational speedup increases with the number of workers.