Spatial undersampling of a wavefield by an array gives rise to visible
grating lobes. If you think of the wavenumber, k, as analogous to angular
frequency, then you must sample the signal at spatial intervals smaller than
π/kmax (or
λmin/2) in order to remove aliasing. The
appearance of visible grating lobes is also known as spatial aliasing. The variable
kmax is the largest wavenumber value present
in the signal.
The directions of maximum spatial response of a ULA are determined by the peaks of the
array’s array pattern (alternatively called the beam
pattern or array factor). Peaks other than the mainlobe
peak are called grating lobes. For a ULA, the array pattern depends only on the wavenumber
component of the wavefield along the array axis (the y-direction for the
phased.ULA
System object). The wavenumber component is related to the look-direction of an arriving
wavefield by ky = –2π sin φ/λ. The angle
φ is the broadside angle—the angle that the look-direction makes
with a plane perpendicular to the array. The look-direction points away from the array to
the wavefield source.
The array pattern possesses an infinite number of periodically-spaced peaks that are
equal in strength to the mainlobe peak. If you steer the array to the
φ0 direction, the array pattern for a ULA has
its mainlobe peak at the wavenumber value of ky0 = –2π sin
φ0/λ. The array pattern has strong grating lobe peaks
at kym = ky0 + 2π m/d, for
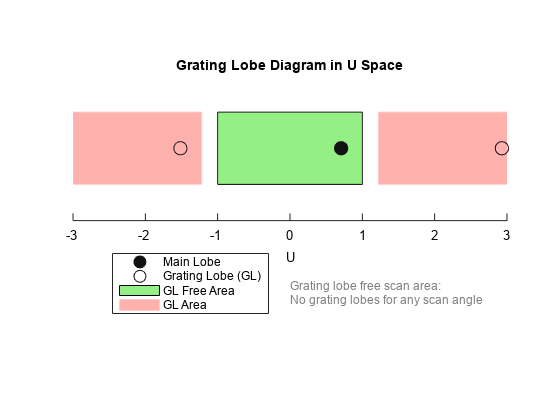
any integer value m. Expressed in terms of direction cosines, the grating
lobes occur at um = u0 +
mλ/d, where u0 = sin
φ0. The direction cosine,
u0, is the cosine of the angle that the
look-direction makes with the y-axis and is equal to sin
φ0 when expressed in terms of the
look-direction.
In order to correspond to a physical look-direction,
um must satisfy, –1 ≤
um ≤ 1. You can compute a physical look-direction angle
φm from sin φm
= um
as long as –1 ≤ um ≤ 1. The spacing of
grating lobes depends upon λ/d. When λ/d is small
enough, multiple grating lobe peaks can correspond to physical look-directions.
The presence or absence of visible grating lobes for the ULA is summarized in this
table.
| Element Spacing | Grating Lobes |
|---|
| λ/d ≥ 2 | No visible grating lobes for any mainlobe direction. |
| 1 ≤ λ/d < 2 | Visible grating lobes can exist for some range of mainlobe
directions. |
| λ/d < 1 | Visible grating lobes exist for every mainlobe direction. |