clusterDBSCAN.discoverClusters
Syntax
Description
[
returns a cluster-ordered list of points, order,reachdist] = clusterDBSCAN.discoverClusters(X,maxepsilon,minnumpoints)order, and the reachability
distances, reachdist, for each point in the data
X. Specify the maximum epsilon, maxepsilon, and
the minimum number of points, minnumpoints. The method implements the
Ordering Points To Identify the Clustering Structure (OPTICS)
algorithm. The OPTICS algorithm is useful when clusters have varying densities.
clusterDBSCAN.discoverClusters(
displays a bar graph representing the cluster hierarchy.X,maxepsilon,minnumpoints)
Examples
Input Arguments
Output Arguments
Algorithms
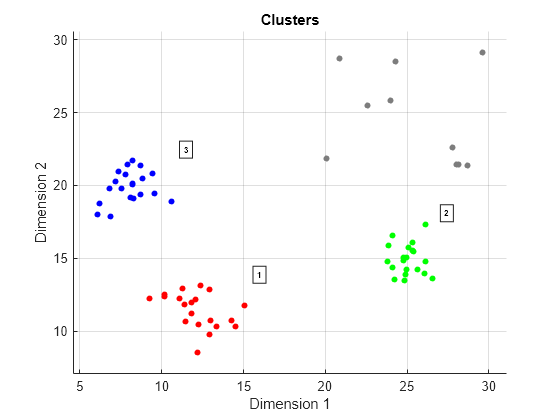
The outputs of clusterDBSCAN.discoverClusters let you create a
reachability-plot from which the hierarchical structure of the clusters can be visualized. A
reachability-plot contains ordered points on the x-axis and the
reachability distances on the y-axis. Use the outputs to examine the
cluster structure over a broad range of parameter settings. You can use the output to help
estimate appropriate epsilon clustering thresholds for the DBSCAN algorithm. Points belonging
to a cluster have small reachability distances to their nearest neighbor, and clusters appear
as valleys in the reachability plot. Deeper valleys correspond to denser clusters. Determine
epsilon from the ordinate of the bottom of the valleys.
OPTICS assumes that dense clusters are entirely contained by less dense clusters. OPTICS processes data in the correct order by tracking the point density neighborhoods. This process is performed by ordering data points by the shortest reachability distances, guaranteeing that clusters with higher density are identified first.
Extended Capabilities
Version History
Introduced in R2021a