Create and Simulate Same Environment in Both MATLAB and Simulink
In this example, you create a MATLAB® implementation of an environment and compare it with different Simulink® implementations of the same environment. This comparison highlights important differences in the agent-environment interaction between MATLAB and Simulink.
This example also shows that, in general, when implementing an environment in Simulink, you have two options:
Output the next observation signal (that is the output function of the next state). This is the approach you follow when calling the step function of a MATLAB environment using a MATLAB Function block. The resulting implementation is equivalent to the way a MATLAB environment works, but requires you to place an Unit Delay block either on each input or on the output of the RL Agent block.
Output the current observation signal (that is the output function of the current state) without using any Unit Delay block.
Although both approaches are equivalent, it is often simpler to use the second one, especially when the next state signal is not available, such as for continuous-time environments.
Fix Random Number Stream for Reproducibility
The example code might involve computation of random numbers at various stages. Fixing the random number stream at the beginning of various sections in the example code preserves the random number sequence in the section every time you run it, and increases the likelihood of reproducing the results. For more information, see Results Reproducibility.
Fix the random number stream with seed 0 and random number algorithm Mersenne Twister. For more information on controlling the seed used for random number generation, see rng.
previousRngState = rng(0,"twister");The output previousRngState is a structure that contains information about the previous state of the stream. You will restore the state at the end of the example.
Create Environment Using MATLAB Functions
To implement an environment, first define the environment observation and action specifications. For this example, both action and observation are a simple numerical scalar.
oinfo = rlNumericSpec([1 1]); ainfo = rlNumericSpec([1 1]);
Use the custom step and reset functions in the supporting files to define the behavior of a simple discrete nonlinear system. For this example, set the reward equal to the observation.
Display the step function, dsStepFcn.m.
type dsStepFcn.mfunction [NextObs,Reward,IsDone,NextState] = dsStepFcn(Action,State) % Advances environment to next state and calculates outputs NextState = 0.9*State + cos(Action); NextObs = NextState^2; Reward = NextObs; IsDone = 0; end
It is important to notice that although there is a direct feedthrough between the action and the next observation, there is no direct feedthrough between the action and the current observation. In other words, the environment is strictly causal from action to observation.
The reset function, dsResetFcn.m, initializes the environment state to 5 and the corresponding initial observation to 25. Display the reset function.
type dsResetFcn.mfunction [InitialObservation, InitialState] = dsResetFcn() % Resets environment to an initial state InitialState = 5; InitialObservation = InitialState^2; end
Use rlFunctionEnv to create a custom environment object.
menv = rlFunctionEnv(oinfo,ainfo,@dsStepFcn,@dsResetFcn);
Create Default Actor-Critic Agent
Create a default actor-critic agent using the environment specifications. To ensure consistency between different simulations, prevent the agent from exploring by setting the UseExplorationPolicy option to false. When you create the agent, the initial parameters of the critic network are initialized with random values. Fix the random number stream so that the agent is always initialized with the same parameter values.
rng(0,"twister");
agentObj = rlACAgent(oinfo,ainfo);
agentObj.UseExplorationPolicy = false;Simulate Agent Using MATLAB Environment
To set the maximum number of simulation steps to six, create an rlSimulationOptions object and set its MaxSteps property to 6.
simopts = rlSimulationOptions(MaxSteps=6);
Then simulate the environment using sim, and collect the experience in the variable mtraj.
mtraj = sim(menv,agentObj,simopts);
Display the action data.
mtraj.Action.act1.Data(:)'
ans = 1×6
2.5540 1.3743 1.2488 1.2252 1.2199 1.2186
Display the observation data.
mtraj.Observation.obs1.Data(:)'
ans = 1×7
25.0000 13.4520 12.2233 11.9928 11.9405 11.9282 11.9253
Call MATLAB Environment from Simulink Using Delays on Observation and Reward
You can use a MATLAB Function (Simulink) block to call the environment step function from Simulink. Assume that both the environment and the agent have a sample time of one second.
Load the Simulink model in memory.
mdl = "dsLoopMLF3";
load_system(mdl);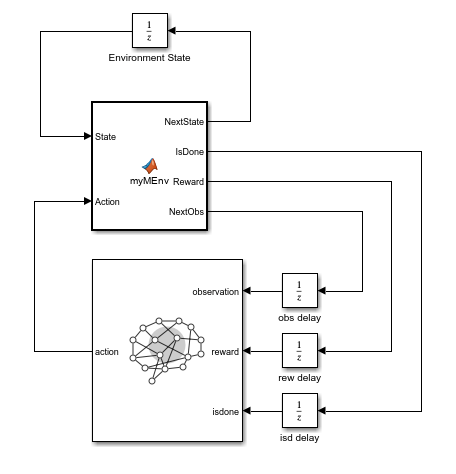
In this model, the RL Agent block is set to use agentObj as an agent. The MATLAB Function block calls the environment step function. In the step function, the order of inputs and outputs are rearranged so that the respective signal lines do not cross each other in Simulink.
function [NextObs,IsDone,Reward,NextState] = myMEnv(Action,State) % Call environment step function [NextObs,Reward,IsDone,NextState] = dsStepFcn(Action,State);
In the model, a Unit Delay block with an initial state set to 5 stores the environment state. This implementation avoids using permanent variables to implement states in the MATLAB Function block, which is subject to various limitations. For more information on these limitations, see the tables in Speed Up Simulation Workflows by Using Model Operating Points (Simulink) and How Stepping Through Simulations Works (Simulink).
The RL Agent block expects the current observation as the input. Therefore, the model uses a delay block, with the Initial condition parameter set to 25, to obtain the current observation. If you instead connect the agent observation port directly to the NextObs environment output, the action signal would be anticipated one step with respect to the MATLAB implementation, which would be incorrect and can also lead to an algebraic loop. For more information on how to deal with algebraic loops see Create Custom Simulink Environments and Algebraic Loop Concepts (Simulink).
Since the reward and is-done signal received by the agent need to be synchronized with the observation signal, the model uses Unit Delay blocks also on the reward and isdone signals to synchronize these signals with the observation signal. The Initial condition parameters of these Unit Delay blocks are set to 25 and 0, respectively.
Create a Simulink environment from the closed-loop Simulink model. First, define block path to the RL Agent block.
blk = mdl + "/RL Agent";Use rlSimulinkEnv to create a Simulink environment.
slenv = rlSimulinkEnv(mdl,blk,oinfo,ainfo);
Use sim to simulate the environment. Collect the resulting experience in the variable straj.
straj = sim(slenv,agentObj,simopts);
Display the action data.
straj.Action.act1.Data(:)'
ans = 1×6
2.5540 1.3743 1.2488 1.2252 1.2199 1.2186
Display the observation data.
straj.Observation.obs1.Data(:)'
ans = 1×7
25.0000 13.4520 12.2233 11.9928 11.9405 11.9282 11.9253
The trajectory is identical to the one obtained from the simulation of the MATLAB environment.
Note that, when you use this approach to calling a MATLAB environment from Simulink, you have to initialize the Unit Delay blocks in a way that is consistent with the initial state of the environment.
Call MATLAB Environment from Simulink Using Delay on Action
You can also call the environment step function by placing a single Unit Delay block on the action signal instead of placing three Unit Delay blocks on the RL Agent block inputs. However, this design results in a closed-loop system that generally starts from a different initial condition, and therefore generates a different trajectory.
For the first episode of training or simulation, you can set the initial condition of the Unit Delay block on the action signal so that the resulting trajectory is the same (just anticipated one step) as the one generated by a MATLAB environment. However, in general, any trajectory that starts from a feasible initial condition is equally valid to train or simulate the agent.
Get the initial value of the action when the observation is equal to 5^2.
a0 = getAction(agentObj,{5^2});Display the value of the initial action.
a0{1}ans = 2.5540
In the following model, dsLoopMLF1.slx, the Initial condition parameter of the Unit Delay block on the action signal is already set to a0{1}.
Load the Simulink model in memory.
mdl = "dsLoopMLF1";
load_system(mdl);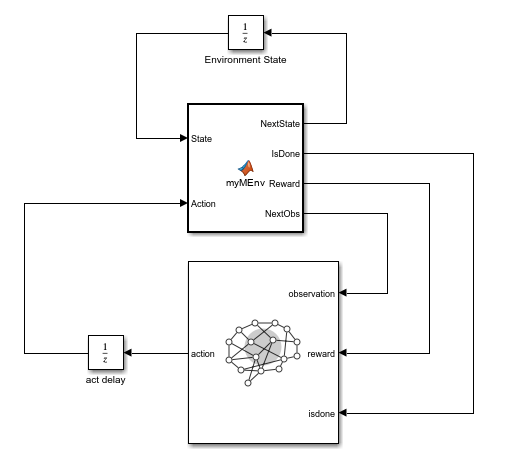
Define the block path to the RL Agent block.
blk = mdl + "/RL Agent";Use rlSimulinkEnv to create a Simulink environment.
slenv = rlSimulinkEnv(mdl,blk,oinfo,ainfo);
Use sim to simulate the environment. Collect the resulting experience in the variable straj.
straj = sim(slenv,agentObj,simopts);
Display the action data.
straj.Action.act1.Data(:)'
ans = 1×6
1.3743 1.2488 1.2252 1.2199 1.2186 1.2183
Display the observation data.
straj.Observation.obs1.Data(:)'
ans = 1×7
13.4520 12.2233 11.9928 11.9405 11.9282 11.9253 11.9246
The trajectory is one time step ahead of the one obtained from the simulation of the MATLAB environment.
Call Separate Environment State and Output Functions from Simulink
If you have separate state and output functions (instead of a single step function), you can call them using separate MATLAB Function (Simulink) blocks, and use an Unit Delay block to represent the environment state.
Display the state function, dsStateFcn.m.
type dsStateFcn.mfunction NextState = dsStateFcn(Action,State) % Advances environment to next state NextState = 0.9*State + cos(Action); end
Display the output function, dsOutputFcn.m.
type dsOutputFcn.mfunction [Observation,Reward,IsDone] = dsOutputFcn(State) % Calculates outputs Observation = State^2; Reward = Observation; IsDone = 0; end
Note that the output does not depend on the current action, because the environment is assumed to be strictly causal.
Load the Simulink model in memory.
mdl = "dsLoopMLF2";
load_system(mdl);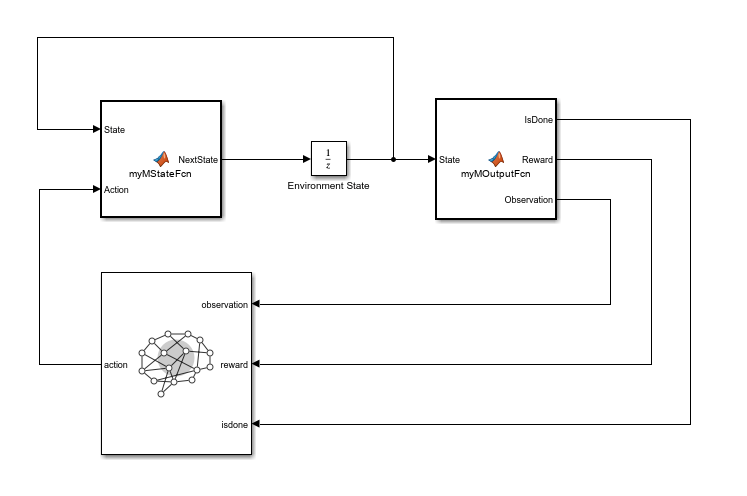
This model uses MATLAB Function (Simulink) blocks to call both functions, and a single Unit Delay block to represent the environment state.
In the first model of this example, you fed the delayed NextObs output signal to the observation input port of the agent block. In this model, instead, the corresponding signal is the delayed output function (in this case, the square) of the NextState output signal. This signal is identical, from the agent perspective, to the output function of the current state signal, which is, in turn, exactly the current observation signal.
In other words, in this model, there is no Unit Delay block on the observation signal because the output function already receives in input the current state instead of the next state (and therefore calculates the current observation instead of the next observation).
Define the block path to the RL Agent block.
blk = mdl + "/RL Agent";Use rlSimulinkEnv to create a Simulink environment.
slenv = rlSimulinkEnv(mdl,blk,oinfo,ainfo);
Use sim to simulate the environment. Collect the resulting experience in the variable straj.
straj = sim(slenv,agentObj,simopts);
Display the action data.
straj.Action.act1.Data(:)'
ans = 1×6
2.5540 1.3743 1.2488 1.2252 1.2199 1.2186
Display the observation data.
straj.Observation.obs1.Data(:)'
ans = 1×7
25.0000 13.4520 12.2233 11.9928 11.9405 11.9282 11.9253
The trajectory is identical to the one obtained from the simulation of the MATLAB environment.
For an example in which a MATLAB environment is called from Simulink using this approach, see Train Multiple Agents for Area Coverage.
Implement Same Environment Using Built-In Simulink Blocks
Instead of calling existing MATLAB environment functions, the dsLoopDSS.slx model directly implements, using built-in Simulink blocks, the discrete-time system defined in the dsStepFcn.m file.
Load the Simulink model in memory.
mdl = "dsLoopSDS";
load_system(mdl);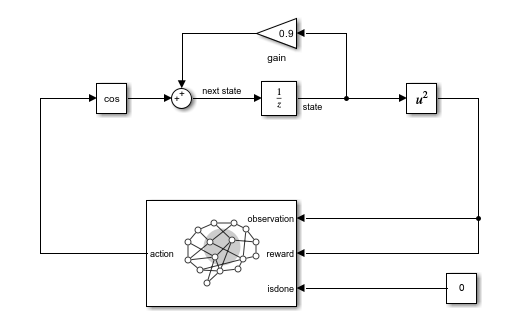
The delayed signal from the NextObs output port in the first example corresponds to delayed square of the next state signal in this model. From the perspective of the agent, this signal is identical to the square of the state signal.
Define the block path to the RL Agent block, and create the environment object.
blk = mdl + "/RL Agent";
slenv = rlSimulinkEnv(mdl,blk,oinfo,ainfo);Simulate the environment, and collect the resulting experience in the variable straj.
straj = sim(slenv,agentObj,simopts);
Display the action data.
straj.Action.act1.Data(:)'
ans = 1×6
2.5540 1.3743 1.2488 1.2252 1.2199 1.2186
Display the observation data.
straj.Observation.obs1.Data(:)'
ans = 1×7
25.0000 13.4520 12.2233 11.9928 11.9405 11.9282 11.9253
As expected, the trajectory is identical to the previous ones.
Implement Same Environment in Continuous-Time
In the csLoop.slx model, the inner linear discrete-time system featured in the dsLoopDSS.slx model is replaced with its continuous-time equivalent.
Load and open the Simulink model with the continuous integrator.
mdl = "csLoop";
load_system(mdl);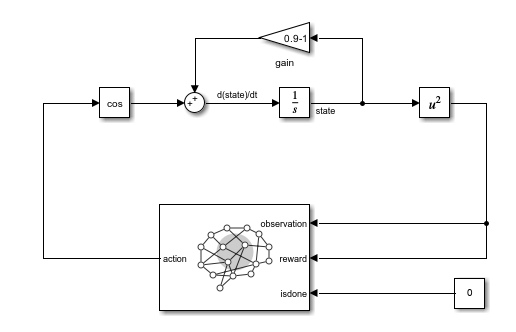
Here, you do not have access to the next state and next observation signals.
Since this is a continuous-time model, it relies on the Simulink solver to perform the integration step. For this example, the fixed-step ODE1 (Euler) solver is selected.
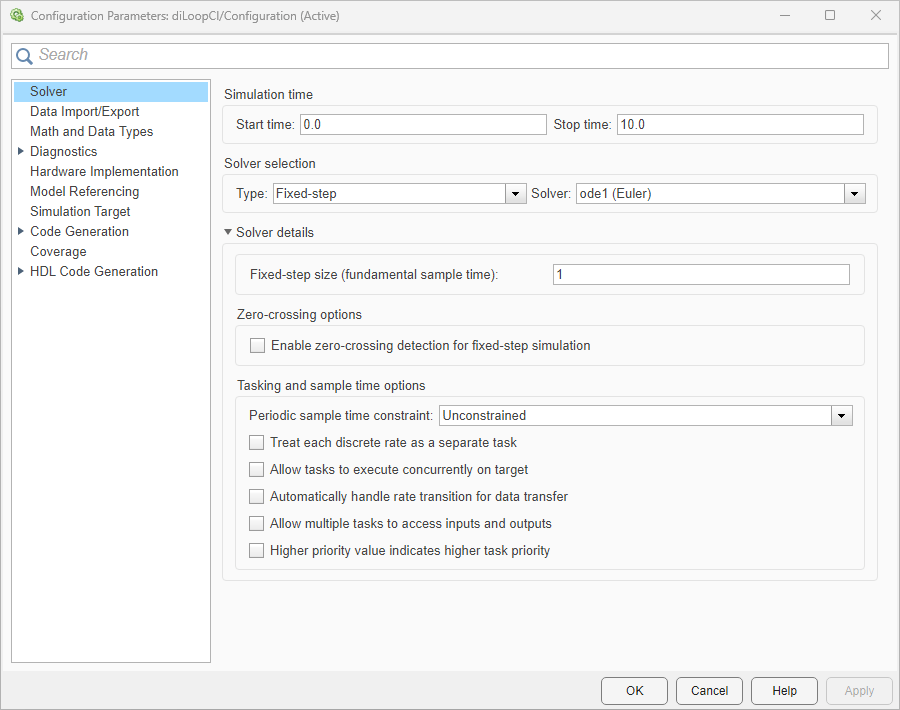
Create the environment object
blk = mdl + "/RL Agent";
slenv = rlSimulinkEnv(mdl,blk,oinfo,ainfo);Simulate the environment, and collect the resulting experience in the variable straj.
straj = sim(slenv,agentObj,simopts);
Display the action data.
straj.Action.act1.Data(:)'
ans = 1×6
2.5540 1.3743 1.2488 1.2252 1.2199 1.2186
Display the observation data.
straj.Observation.obs1.Data(:)'
ans = 1×7
25.0000 13.4520 12.2233 11.9928 11.9405 11.9282 11.9253
The trajectory is identical to the previous ones.
Restore the random number stream using the information stored in previousRngState.
rng(previousRngState);
See Also
Blocks
- MATLAB Function (Simulink)