quaternion

Create quaternion array

Description

A quaternion is a four-part hyper-complex number used in three-dimensional rotations and orientations.

A quaternion number is represented in the form $$a+b\text{i}+c\text{j}+d\text{k}$$, where a, b, c, and d parts are real numbers, and i, j, and k are the basis elements, satisfying the equation: i² = j² = k² = ijk = −1.

The set of quaternions, denoted by H, is defined within a four-dimensional vector space over the real numbers, R⁴. Every element of H has a unique representation based on a linear combination of the basis elements, i, j, and k.

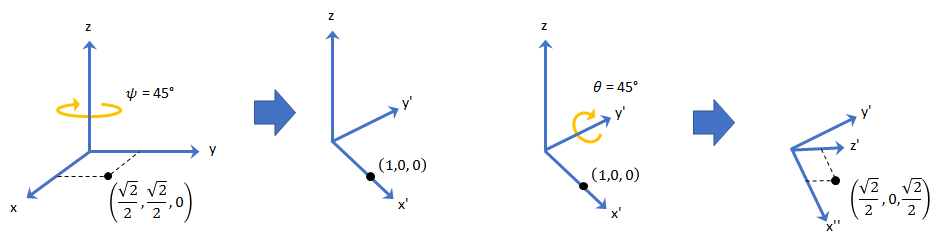
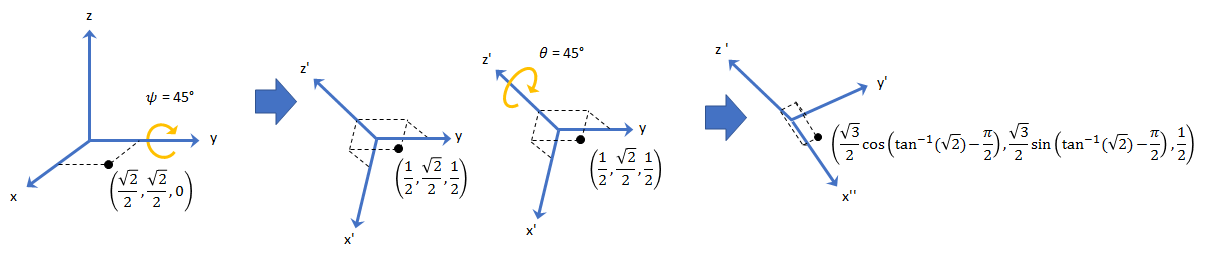
All rotations in 3-D can be described by an axis of rotation and angle about that axis. An advantage of quaternions over rotation matrices is that the axis and angle of rotation is easy to interpret. For example, consider a point in R³. To rotate the point, you define an axis of rotation and an angle of rotation.

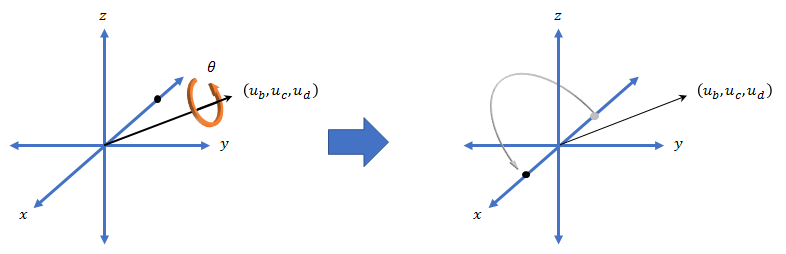
The quaternion representation of the rotation may be expressed as $$q=\cos \left(\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)+\sin \left(\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\left(u_b\text{i}+u_c\text{j}+u_d\text{k}\right)$$, where θ is the angle of rotation and [u_b, u_c, and u_d] is the axis of rotation.

Creation

Syntax

quat = quaternion()

quat = quaternion(A,B,C,D)

quat = quaternion(matrix)

quat = quaternion(RV,"rotvec")

quat = quaternion(RV,"rotvecd")

quat = quaternion(RM,"rotmat",PF)

quat = quaternion(E,"euler",RS,PF)

quat = quaternion(E,"eulerd",RS,PF)

quat = quaternion(transformation)

quat = quaternion(rotation)

Description

quat = quaternion() creates an empty quaternion.

quat = quaternion(A,B,C,D) creates a quaternion array where the four quaternion parts are taken from the arrays A, B, C, and D. All the inputs must have the same size and be of the same data type.

quat = quaternion(matrix) creates an N-by-1 quaternion array from an N-by-4 matrix, where each column becomes one part of the quaternion.

quat = quaternion(RV,"rotvec") creates an N-by-1 quaternion array from an N-by-3 matrix of rotation vectors, RV. Each row of RV represents a rotation vector in radians.

quat = quaternion(RV,"rotvecd") creates an N-by-1 quaternion array from an N-by-3 matrix of rotation vectors, RV. Each row of RV represents a rotation vector in degrees.

quat = quaternion(RM,"rotmat",PF) creates an N-by-1 quaternion array from the 3-by-3-by-N array of rotation matrices, RM. PF can be either "point" if the Euler angles represent point rotations or "frame" for frame rotations.

quat = quaternion(E,"euler",RS,PF) creates an N-by-1 quaternion array from the N-by-3 matrix, E. Each row of E represents a set of Euler angles in radians. The angles in E are rotations about the axes in sequence RS.

quat = quaternion(E,"eulerd",RS,PF) creates an N-by-1 quaternion array from the N-by-3 matrix, E. Each row of E represents a set of Euler angles in degrees. The angles in E are rotations about the axes in sequence RS.

quat = quaternion(transformation) creates a quaternion array from the SE(3) transformation transformation.

quat = quaternion(rotation) creates an quaternion array from the SO(3) rotation rotation.

Input Arguments

A,B,C,D — Quaternion parts

comma-separated arrays of the same size

Parts of a quaternion, specified as four comma-separated scalars, matrices, or multi-dimensional arrays of the same size.

Example: quat = quaternion(1,2,3,4) creates a quaternion of the form 1 + 2i + 3j + 4k.

Example: quat = quaternion([1,5],[2,6],[3,7],[4,8]) creates a 1-by-2 quaternion array where quat(1,1) = 1 + 2i + 3j + 4k and quat(1,2) = 5 + 6i + 7j + 8k

Data Types: single | double

matrix — Matrix of quaternion parts

N-by-4 matrix

Matrix of quaternion parts, specified as an N-by-4 matrix. Each row represents a separate quaternion. Each column represents a separate quaternion part.

Example: quat = quaternion(rand(10,4)) creates a 10-by-1 quaternion array.

Data Types: single | double

RV — Matrix of rotation vectors

N-by-3 matrix

Matrix of rotation vectors, specified as an N-by-3 matrix. Each row of RV represents the [X Y Z] elements of a rotation vector. A rotation vector is a unit vector representing the axis of rotation scaled by the angle of rotation in radians or degrees.

To use this syntax, specify the first argument as a matrix of rotation vectors and the second argument as the "rotvec" or "rotvecd".

Example: quat = quaternion(rand(10,3),"rotvec") creates a 10-by-1 quaternion array.

Data Types: single | double

RM — Rotation matrices

3-by-3 matrix | 3-by-3-by-N array

Array of rotation matrices, specified by a 3-by-3 matrix or 3-by-3-by-N array. Each page of the array represents a separate rotation matrix.

Example: quat = quaternion(rand(3),"rotmat","point")

Example: quat = quaternion(rand(3),"rotmat","frame")

Data Types: single | double

PF — Type of rotation matrix

"point" | "frame"

Type of rotation matrix, specified by "point" or "frame".

Example: quat = quaternion(rand(3),"rotmat","point")

Example: quat = quaternion(rand(3),"rotmat","frame")

Data Types: char | string

E — Matrix of Euler angles

N-by-3 matrix

Matrix of Euler angles, specified by an N-by-3 matrix. If using the "euler" syntax, specify E in radians. If using the "eulerd" syntax, specify E in degrees.

Example: quat = quaternion(E,"euler","YZY","point")

Example: quat = quaternion(E,"euler","XYZ","frame")

Data Types: single | double

RS — Rotation sequence

character vector | scalar string

Rotation sequence, specified as a three-element character vector:

• "YZY"

• "YXY"

• "ZYZ"

• "ZXZ"

• "XYX"

• "XZX"

• "XYZ"

• "YZX"

• "ZXY"

• "XZY"

• "ZYX"

• "YXZ"

Assume you want to determine the new coordinates of a point when its coordinate system is rotated using frame rotation. The point is defined in the original coordinate system as:

point = [sqrt(2)/2,sqrt(2)/2,0];

In this representation, the first column represents the x-axis, the second column represents the y-axis, and the third column represents the z-axis.

You want to rotate the point using the Euler angle representation [45,45,0]. Rotate the point using two different rotation sequences:

• If you create a quaternion rotator and specify the "ZYX" sequence, the frame is first rotated 45° around the z-axis, then 45° around the new y-axis.

  quatRotator = quaternion([45,45,0],"eulerd","ZYX","frame");
  newPointCoordinate = rotateframe(quatRotator,point)

  newPointCoordinate =
  
      0.7071   -0.0000    0.7071

  

• If you create a quaternion rotator and specify the "YZX" sequence, the frame is first rotated 45° around the y-axis, then 45° around the new z-axis.

  quatRotator = quaternion([45,45,0],"eulerd","YZX","frame");
  newPointCoordinate = rotateframe(quatRotator,point)

  newPointCoordinate =
  
      0.8536    0.1464    0.5000

  

Data Types: char | string

transformation — Homogeneous transformation

se3 object | N-element array of se3 objects

Transformation, specified as an se3 object, or as an N-element array of se3 objects. N is the total number of transformations.

The quaternion object ignores the translational component of the transformation and converts the rotational 3-by-3 submatrix of the transformation to a quaternion.

rotation — Orthonormal rotation

so3 object | N-element array of so3 objects

Orthonormal rotation, specified as an so3 object, or as an N-element array of so3 objects. N is the total number of rotations.

Object Functions

angvel	Angular velocity from quaternion array
classUnderlying	Class of parts within quaternion
compact	Convert quaternion array to N-by-4 matrix
conj	Complex conjugate of quaternion
'	Complex conjugate transpose of quaternion array
dist	Angular distance in radians
euler	Convert quaternion to Euler angles (radians)
eulerd	Convert quaternion to Euler angles (degrees)
exp	Exponential of quaternion array
.\,ldivide	Element-wise quaternion left division
log	Natural logarithm of quaternion array
meanrot	Quaternion mean rotation
-	Quaternion subtraction
*	Quaternion multiplication
norm	Quaternion norm
normalize	Quaternion normalization
ones	Create quaternion array with real parts set to one and imaginary parts set to zero
parts	Extract quaternion parts
.^,power	Element-wise quaternion power
prod	Product of quaternion array
randrot	Uniformly distributed random rotations
./,rdivide	Element-wise quaternion right division
rotateframe	Quaternion frame rotation
rotatepoint	Quaternion point rotation
rotmat	Convert quaternion to rotation matrix
rotvec	Convert quaternion to rotation vector (radians)
rotvecd	Convert quaternion to rotation vector (degrees)
slerp	Spherical linear interpolation
.*,times	Element-wise quaternion multiplication
'	Transpose quaternion array
-	Quaternion unary minus
zeros	Create quaternion array with all parts set to zero

Examples

Create Empty Quaternion

quat = quaternion()

quat = 

  0x0 empty quaternion array

By default, the underlying class of the quaternion is a double.

classUnderlying(quat)

ans = 
'double'

Create Quaternion by Specifying Individual Quaternion Parts

You can create a quaternion array by specifying the four parts as comma-separated scalars, matrices, or multidimensional arrays of the same size.

Define quaternion parts as scalars.

A = 1.1;
B = 2.1;
C = 3.1;
D = 4.1;
quatScalar = quaternion(A,B,C,D)

quatScalar = quaternion
     1.1 + 2.1i + 3.1j + 4.1k

Define quaternion parts as column vectors.

A = [1.1;1.2];
B = [2.1;2.2];
C = [3.1;3.2];
D = [4.1;4.2];
quatVector = quaternion(A,B,C,D)

quatVector = 2x1 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k
     1.2 + 2.2i + 3.2j + 4.2k

Define quaternion parts as matrices.

A = [1.1,1.3; ...
     1.2,1.4];
B = [2.1,2.3; ...
     2.2,2.4];
C = [3.1,3.3; ...
     3.2,3.4];
D = [4.1,4.3; ...
     4.2,4.4];
quatMatrix = quaternion(A,B,C,D)

quatMatrix = 2x2 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k     1.3 + 2.3i + 3.3j + 4.3k
     1.2 + 2.2i + 3.2j + 4.2k     1.4 + 2.4i + 3.4j + 4.4k

Define quaternion parts as three dimensional arrays.

A = randn(2,2,2);
B = zeros(2,2,2);
C = zeros(2,2,2);
D = zeros(2,2,2);
quatMultiDimArray = quaternion(A,B,C,D)

quatMultiDimArray = 2x2x2 quaternion array
quatMultiDimArray(:,:,1) = 

     0.53767 +       0i +       0j +       0k     -2.2588 +       0i +       0j +       0k
      1.8339 +       0i +       0j +       0k     0.86217 +       0i +       0j +       0k


quatMultiDimArray(:,:,2) = 

     0.31877 +       0i +       0j +       0k    -0.43359 +       0i +       0j +       0k
     -1.3077 +       0i +       0j +       0k     0.34262 +       0i +       0j +       0k

Create Quaternion by Specifying Quaternion Parts Matrix

You can create a scalar or column vector of quaternions by specify an N-by-4 matrix of quaternion parts, where columns correspond to the quaternion parts A, B, C, and D.

Create a column vector of random quaternions.

quatParts = rand(3,4)

quatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

quat = quaternion(quatParts)

quat = 3x1 quaternion array
     0.81472 + 0.91338i +  0.2785j + 0.96489k
     0.90579 + 0.63236i + 0.54688j + 0.15761k
     0.12699 + 0.09754i + 0.95751j + 0.97059k

To retrieve the quatParts matrix from quaternion representation, use compact.

retrievedquatParts = compact(quat)

retrievedquatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

Create Quaternion by Specifying Rotation Vectors

You can create an N-by-1 quaternion array by specifying an N-by-3 matrix of rotation vectors in radians or degrees. Rotation vectors are compact spatial representations that have a one-to-one relationship with normalized quaternions.

Rotation Vectors in Radians

Create a scalar quaternion using a rotation vector and verify the resulting quaternion is normalized.

rotationVector = [0.3491,0.6283,0.3491];
quat = quaternion(rotationVector,"rotvec")

quat = quaternion
     0.92124 + 0.16994i + 0.30586j + 0.16994k

norm(quat)

ans = 1.0000

You can convert from quaternions to rotation vectors in radians using the rotvec function. Recover the rotationVector from the quaternion, quat.

rotvec(quat)

ans = 1×3

    0.3491    0.6283    0.3491

Rotation Vectors in Degrees

Create a scalar quaternion using a rotation vector and verify the resulting quaternion is normalized.

rotationVector = [20,36,20];
quat = quaternion(rotationVector,"rotvecd")

quat = quaternion
     0.92125 + 0.16993i + 0.30587j + 0.16993k

norm(quat)

ans = 1

You can convert from quaternions to rotation vectors in degrees using the rotvecd function. Recover the rotationVector from the quaternion, quat.

rotvecd(quat)

ans = 1×3

   20.0000   36.0000   20.0000

Create Quaternion by Specifying Rotation Matrices

You can create an N-by-1 quaternion array by specifying a 3-by-3-by-N array of rotation matrices. Each page of the rotation matrix array corresponds to one element of the quaternion array.

Create a scalar quaternion using a 3-by-3 rotation matrix. Specify whether the rotation matrix should be interpreted as a frame or point rotation.

rotationMatrix = [1 0         0; ...
                  0 sqrt(3)/2 0.5; ...
                  0 -0.5      sqrt(3)/2];
quat = quaternion(rotationMatrix,"rotmat","frame")

quat = quaternion
     0.96593 + 0.25882i +       0j +       0k

You can convert from quaternions to rotation matrices using the rotmat function. Recover the rotationMatrix from the quaternion, quat.

rotmat(quat,"frame")

ans = 3×3

    1.0000         0         0
         0    0.8660    0.5000
         0   -0.5000    0.8660

Create Quaternion by Specifying Euler Angles

You can create an N-by-1 quaternion array by specifying an N-by-3 array of Euler angles in radians or degrees.

Euler Angles in Radians

Use the euler syntax to create a scalar quaternion using a 1-by-3 vector of Euler angles in radians. Specify the rotation sequence of the Euler angles and whether the angles represent a frame or point rotation.

E = [pi/2,0,pi/4];
quat = quaternion(E,"euler","ZYX","frame")

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

You can convert from quaternions to Euler angles using the euler function. Recover the Euler angles, E, from the quaternion, quat.

euler(quat,"ZYX","frame")

ans = 1×3

    1.5708         0    0.7854

Euler Angles in Degrees

Use the eulerd syntax to create a scalar quaternion using a 1-by-3 vector of Euler angles in degrees. Specify the rotation sequence of the Euler angles and whether the angles represent a frame or point rotation.

E = [90,0,45];
quat = quaternion(E,"eulerd","ZYX","frame")

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

You can convert from quaternions to Euler angles in degrees using the eulerd function. Recover the Euler angles, E, from the quaternion, quat.

eulerd(quat,"ZYX","frame")

ans = 1×3

   90.0000         0   45.0000

Quaternion Algebra

Quaternions form a noncommutative associative algebra over the real numbers. This example illustrates the rules of quaternion algebra.

Addition and Subtraction

Quaternion addition and subtraction occur part-by-part, and are commutative:

Q1 = quaternion(1,2,3,4)

Q1 = quaternion
     1 + 2i + 3j + 4k

Q2 = quaternion(9,8,7,6)

Q2 = quaternion
     9 + 8i + 7j + 6k

Q1plusQ2 = Q1 + Q2

Q1plusQ2 = quaternion
     10 + 10i + 10j + 10k

Q2plusQ1 = Q2 + Q1

Q2plusQ1 = quaternion
     10 + 10i + 10j + 10k

Q1minusQ2 = Q1 - Q2

Q1minusQ2 = quaternion
    -8 - 6i - 4j - 2k

Q2minusQ1 = Q2 - Q1

Q2minusQ1 = quaternion
     8 + 6i + 4j + 2k

You can also perform addition and subtraction of real numbers and quaternions. The first part of a quaternion is referred to as the real part, while the second, third, and fourth parts are referred to as the vector. Addition and subtraction with real numbers affect only the real part of the quaternion.

Q1plusRealNumber = Q1 + 5

Q1plusRealNumber = quaternion
     6 + 2i + 3j + 4k

Q1minusRealNumber = Q1 - 5

Q1minusRealNumber = quaternion
    -4 + 2i + 3j + 4k

Multiplication

Quaternion multiplication is determined by the products of the basis elements and the distributive law. Recall that multiplication of the basis elements, i, j, and k, are not commutative, and therefore quaternion multiplication is not commutative.

Q1timesQ2 = Q1 * Q2

Q1timesQ2 = quaternion
    -52 + 16i + 54j + 32k

Q2timesQ1 = Q2 * Q1

Q2timesQ1 = quaternion
    -52 + 36i + 14j + 52k

isequal(Q1timesQ2,Q2timesQ1)

ans = logical
   0

You can also multiply a quaternion by a real number. If you multiply a quaternion by a real number, each part of the quaternion is multiplied by the real number individually:

Q1times5 = Q1*5

Q1times5 = quaternion
      5 + 10i + 15j + 20k

Multiplying a quaternion by a real number is commutative.

isequal(Q1*5,5*Q1)

ans = logical
   1

Conjugation

The complex conjugate of a quaternion is defined such that each element of the vector portion of the quaternion is negated.

Q1

Q1 = quaternion
     1 + 2i + 3j + 4k

conj(Q1)

ans = quaternion
     1 - 2i - 3j - 4k

Multiplication between a quaternion and its conjugate is commutative:

isequal(Q1*conj(Q1),conj(Q1)*Q1)

ans = logical
   1

Quaternion Array Manipulation

You can organize quaternions into vectors, matrices, and multidimensional arrays. Built-in MATLAB® functions have been enhanced to work with quaternions.

Concatenate

Quaternions are treated as individual objects during concatenation and follow MATLAB rules for array manipulation.

Q1 = quaternion(1,2,3,4);
Q2 = quaternion(9,8,7,6);

qVector = [Q1,Q2]

qVector = 1x2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k

Q3 = quaternion(-1,-2,-3,-4);
Q4 = quaternion(-9,-8,-7,-6);

qMatrix = [qVector;Q3,Q4]

qMatrix = 2x2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMultiDimensionalArray(:,:,1) = qMatrix;
qMultiDimensionalArray(:,:,2) = qMatrix

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

Indexing

To access or assign elements in a quaternion array, use indexing.

qLoc2 = qMultiDimensionalArray(2)

qLoc2 = quaternion
    -1 - 2i - 3j - 4k

Replace the quaternion at index two with a quaternion one.

qMultiDimensionalArray(2) = ones("quaternion")

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

Reshape

To reshape quaternion arrays, use the reshape function.

qMatReshaped = reshape(qMatrix,4,1)

qMatReshaped = 4x1 quaternion array
     1 + 2i + 3j + 4k
    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k
    -9 - 8i - 7j - 6k

Transpose

To transpose quaternion vectors and matrices, use the transpose function.

qMatTransposed = transpose(qMatrix)

qMatTransposed = 2x2 quaternion array
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

Permute

To permute quaternion vectors, matrices, and multidimensional arrays, use the permute function.

qMultiDimensionalArray

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMatPermute = permute(qMultiDimensionalArray,[3,1,2])

qMatPermute = 2x2x2 quaternion array
qMatPermute(:,:,1) = 

     1 + 2i + 3j + 4k     1 + 0i + 0j + 0k
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k


qMatPermute(:,:,2) = 

     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2018a