Robust Controller Design
This example shows how to design a feedback controller for a plant with uncertain parameters and uncertain model dynamics. The goals of the controller design are good steady-state tracking and disturbance-rejection properties.
Design a controller for the plant G described in Robust Controller Design. This plant is a first-order system with an uncertain time constant. The plant also has some uncertain dynamic deviations from first-order behavior beyond about 9 rad/s.
bw = ureal('bw',5,'Percentage',10); Gnom = tf(1,[1/bw 1]); W = makeweight(.05,9,10); Delta = ultidyn('Delta',[1 1]); G = Gnom*(1+W*Delta)
Uncertain continuous-time state-space model with 1 outputs, 1 inputs, 2 states. The model uncertainty consists of the following blocks: Delta: Uncertain 1x1 LTI, peak gain = 1, 1 occurrences bw: Uncertain real, nominal = 5, variability = [-10,10]%, 1 occurrences Model Properties Type "G.NominalValue" to see the nominal value and "G.Uncertainty" to interact with the uncertain elements.
Design Controller
Because of the nominal first-order behavior of the plant, choose a PI control architecture. For a desired closed-loop damping ratio ξ and natural frequency , the design equations for the proportional and integral gains (based on the nominal open-loop time constant of 0.2) are:
To study how the uncertainty in G affects the achievable closed-loop bandwidth, design two controllers, both achieving ξ = 0.707, but with different values, 3 and 7.5.
xi = 0.707; wn1 = 3; wn2 = 7.5; Kp1 = 2*xi*wn1/5 - 1; Ki1 = (wn1^2)/5; C1 = tf([Kp1,Ki1],[1 0]); Kp2 = 2*xi*wn2/5 - 1; Ki2 = (wn2^2)/5; C2 = tf([Kp2,Ki2],[1 0]);
Examine Controller Performance
The nominal closed-loop bandwidth achieved by C2 is in a region where G has significant model uncertainty. It is therefore expected that the model variations cause significant degradations in the closed-loop performance with that controller. To examine the performance, form the closed-loop systems and plot the step responses of samples of the resulting systems.
T1 = feedback(G*C1,1); T2 = feedback(G*C2,1); tfinal = 3; step(T1,'b',T2,'r',tfinal)

The step responses for T2 exhibit a faster rise time because C2 sets a higher closed-loop bandwidth. However, as expected, the model variations have a greater impact.
You can use robstab to check the robustness of the stability of the closed-loop systems to model variations.
opt = robOptions('Display','on'); stabmarg1 = robstab(T1,opt);
Computing peak... Percent completed: 100/100 System is robustly stable for the modeled uncertainty. -- It can tolerate up to 401% of the modeled uncertainty. -- There is a destabilizing perturbation amounting to 401% of the modeled uncertainty. -- This perturbation causes an instability at the frequency 3.74 rad/seconds.
stabmarg2 = robstab(T2,opt);
Computing peak... Percent completed: 100/100 System is robustly stable for the modeled uncertainty. -- It can tolerate up to 125% of the modeled uncertainty. -- There is a destabilizing perturbation amounting to 125% of the modeled uncertainty. -- This perturbation causes an instability at the frequency 11.4 rad/seconds.
The display gives the amount of uncertainty that the system can tolerate without going unstable. In both cases, the closed-loop systems can tolerate more than 100% of the modeled uncertainty range while remaining stable. stabmarg contains lower and upper bounds on the stability margin. A stability margin greater than 1 means the system is stable for all values of the modeled uncertainty. A stability margin less than 1 means there are allowable values of the uncertain elements that make the system unstable.
Compare Nominal and Worst-Case Behavior
While both systems are stable for all variations, their performance is affected to different degrees. To determine how the uncertainty affects closed-loop performance, you can use wcgain to compute the worst-case effect of the uncertainty on the peak magnitude of the closed-loop sensitivity function, S = 1/(1+GC). This peak gain of this function is typically correlated with the amount of overshoot in a step response; peak gain greater than one indicates overshoot.
Form the closed-loop sensitivity functions and call wcgain.
S1 = feedback(1,G*C1); S2 = feedback(1,G*C2); [maxgain1,wcu1] = wcgain(S1); [maxgain2,wcu2] = wcgain(S2);
maxgain gives lower and upper bounds on the worst-case peak gain of the sensitivity transfer function, as well as the specific frequency where the maximum gain occurs. Examine the bounds on the worst-case gain for both systems.
maxgain1
maxgain1 = struct with fields:
LowerBound: 1.8831
UpperBound: 1.8861
CriticalFrequency: 3.1938
maxgain2
maxgain2 = struct with fields:
LowerBound: 4.6286
UpperBound: 4.6378
CriticalFrequency: 11.6132
wcu contains the particular values of the uncertain elements that achieve this worst-case behavior. Use usubs to substitute these worst-case values for uncertain elements, and compare the nominal and worst-case behavior.
wcS1 = usubs(S1,wcu1); wcS2 = usubs(S2,wcu2); bodemag(S1.NominalValue,'b',wcS1,'b'); hold on bodemag(S2.NominalValue,'r',wcS2,'r');
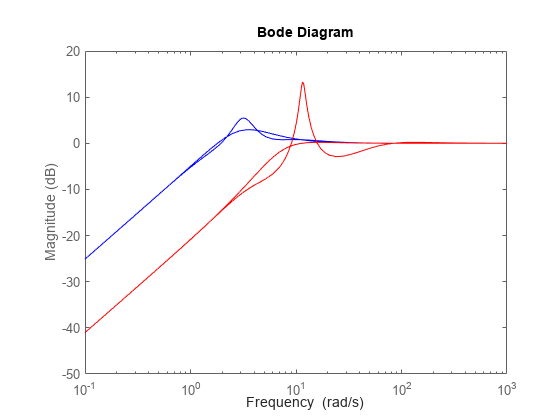
While C2 achieves better nominal sensitivity than C1, the nominal closed-loop bandwidth extends too far into the frequency range where the process uncertainty is very large. Hence the worst-case performance of C2 is inferior to C1 for this particular uncertain model.