Comparison of Orbit Propagators
This example compares the orbits predicted by the Two-Body-Keplerian and Simplified General Perturbations-4 (SGP4) orbit propagators. An orbit propagator is a solver that calculates the position and velocity of an object in space, primarily influenced by gravitational field of the celestial bodies.
The Two-Body-Keplerian orbit propagator relies on a simplified model that considers only the gravitational field of the Earth and ignores the effects of other celestial bodies and environmental factors. This model assumes that the Earth is spherical with a uniform density. This approach makes this propagator the least accurate among the models discussed.
In contrast, the SGP4 orbit propagator incorporates both secular and periodic orbital disturbances due to the Earth's shape and atmospheric drag, making it suitable for satellites in near-Earth orbit with orbital periods less than 225 minutes. When the orbital period of the satellite is greater than 225 minutes, the SGP4 orbit propagator additionally accounts for solar and lunar gravity.
Create a Satellite Scenario
Create a satellite scenario by using the satelliteScenario function. Set the start time to 11-May-2020 12:35:38 PM UTC, and the stop time to 13-May-2020 12:35:38 PM UTC, by using the datetime function. Set the sample time to 60 seconds.
startTime = datetime(2020,5,11,12,35,38); stopTime = startTime + days(2); sampleTime = 60; sc = satelliteScenario(startTime,stopTime,sampleTime)
sc =
satelliteScenario with properties:
StartTime: 11-May-2020 12:35:38
StopTime: 13-May-2020 12:35:38
SampleTime: 60
AutoSimulate: 1
CentralBodyOptions: [1×1 Aero.satellitescenario.CentralBodyOptions]
Satellites: [1×0 matlabshared.satellitescenario.Satellite]
GroundStations: [1×0 matlabshared.satellitescenario.GroundStation]
Platforms: [1×0 matlabshared.satellitescenario.Platform]
Viewers: [0×0 matlabshared.satellitescenario.Viewer]
AutoShow: 1
Add Satellites to the Satellite Scenario
Add two satellites to the satellite scenario from the two-line element (TLE) file eccentricOrbitSatellite.tle by using the satellite function. TLE is a data format used for encoding the orbital elements of an Earth-orbiting object defined at a specific time. Assign a Two-Body-Keplerian orbit propagator to the first satellite and SGP4 to the second satellite.
tleFile = "eccentricOrbitSatellite.tle"; satTwoBodyKeplerian = satellite(sc,tleFile, ... "Name","satTwoBodyKeplerian", ... "OrbitPropagator","two-body-keplerian")
satTwoBodyKeplerian =
Satellite with properties:
Name: satTwoBodyKeplerian
ID: 1
ConicalSensors: [1x0 matlabshared.satellitescenario.ConicalSensor]
Gimbals: [1x0 matlabshared.satellitescenario.Gimbal]
Transmitters: [1x0 satcom.satellitescenario.Transmitter]
Receivers: [1x0 satcom.satellitescenario.Receiver]
Accesses: [1x0 matlabshared.satellitescenario.Access]
Eclipse: [1x0 Aero.satellitescenario.Eclipse]
GroundTrack: [1x1 matlabshared.satellitescenario.GroundTrack]
Orbit: [1x1 matlabshared.satellitescenario.Orbit]
CoordinateAxes: [1x1 matlabshared.satellitescenario.CoordinateAxes]
OrbitPropagator: two-body-keplerian
MarkerColor: [0.059 1 1]
MarkerSize: 6
ShowLabel: true
LabelFontColor: [1 1 1]
LabelFontSize: 15
Visual3DModel:
Visual3DModelScale: 1
satSGP4 = satellite(sc,tleFile, ... "Name","satSGP4", ... "OrbitPropagator","sgp4")
satSGP4 =
Satellite with properties:
Name: satSGP4
ID: 2
ConicalSensors: [1x0 matlabshared.satellitescenario.ConicalSensor]
Gimbals: [1x0 matlabshared.satellitescenario.Gimbal]
Transmitters: [1x0 satcom.satellitescenario.Transmitter]
Receivers: [1x0 satcom.satellitescenario.Receiver]
Accesses: [1x0 matlabshared.satellitescenario.Access]
Eclipse: [1x0 Aero.satellitescenario.Eclipse]
GroundTrack: [1x1 matlabshared.satellitescenario.GroundTrack]
Orbit: [1x1 matlabshared.satellitescenario.Orbit]
CoordinateAxes: [1x1 matlabshared.satellitescenario.CoordinateAxes]
OrbitPropagator: sgp4
MarkerColor: [0.059 1 1]
MarkerSize: 6
ShowLabel: true
LabelFontColor: [1 1 1]
LabelFontSize: 15
Visual3DModel:
Visual3DModelScale: 1
Visualize the Satellites and their Orbits
Launch a satellite scenario viewer and visualize the satellite scenario by using the satelliteScenarioViewer function. Set the visualizations of satSGP4 to green.
v = satelliteScenarioViewer(sc); satSGP4.MarkerColor = "green"; satSGP4.Orbit.LineColor = "green"; satSGP4.LabelFontColor = "green";

Focus the camera on satTwoBodyKeplerian by using the camtarget function.
camtarget(v,satTwoBodyKeplerian);
Left-click anywhere inside the satellite scenario viewer window and move the mouse while holding the click to pan the camera. Adjust the zoom level using the scroll wheel to bring all three satellites into view.

Visualize a Dynamic Animation of the Satellite Movement
Visualize the movement of the satellites by using the play function on the satellite scenario. The play function simulates the satellite scenario from the specified StartTime to StopTime using a step size specified by SampleTime, and plays the results on the satellite scenario viewer.
play(sc)
Use the playback controls located at the bottom of the satellite scenario viewer window to control the playback speed and direction. Focus the camera again on satTwoBodyKeplerian by using the camtarget function, and bring all three satellites into view by adjusting the zoom level.
camtarget(v,satTwoBodyKeplerian);
The positions of the three satellites diverge over time.

Obtain the Position and Velocity History of the Satellites
Return the position and velocity history of the satellites in the Geocentric Celestial Reference Frame (GCRF) by using the states function.
[positionTwoBodyKeplerian,velocityTwoBodyKeplerian,time] = states(satTwoBodyKeplerian); [positionSGP4,velocitySGP4] = states(satSGP4);
Plot Magnitude of Relative Position with Respect to Two-Body-Keplerian Prediction
Calculate the magnitude of the relative position of satSGP4 with respect to satTwoBodyKeplerian by using the vecnorm function.
sgp4RelativePosition = vecnorm(positionSGP4 - positionTwoBodyKeplerian,2,1);
Plot the magnitude of the relative position in kilometers of satSGP4 with respect to that of satTwoBodyKeplerian by using the plot function.
sgp4RelativePositionKm = sgp4RelativePosition/1000; plot(time,sgp4RelativePositionKm) xlabel("Time") ylabel("Relative position (km)") grid on
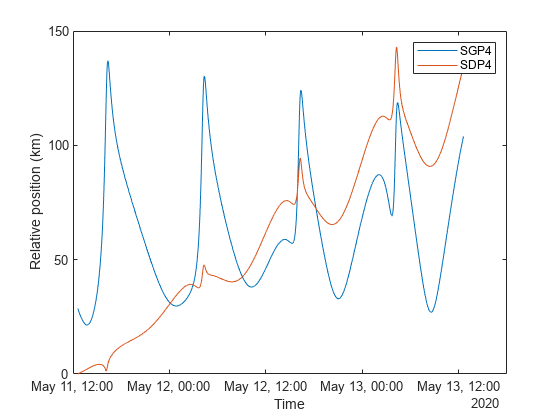
Over time, the position of satSGP4 deviates from that of satTwoBodyKeplerian because satSGP4 accounts for secular and periodic orbital perturbations caused by Earth's geometry and atmospheric drag. Because the orbital period calculated from the TLE file is greater than 225 minutes, the position of satSGP4 also accounts for solar and lunar gravity. You can get the orbital period using the orbitalElements function.
elSatSGP4 = orbitalElements(satSGP4);
elSatSGP4.Period/60 % minutesans = 720
The position of satTwoBodyKeplerian assumes a spherical gravitational potential around Earth and ignores all perturbation effects.
Plot Magnitude of Relative Velocity with Respect to Two-Body-Keplerian Prediction
Calculate the magnitude of the relative velocity of satSGP4 with respect to satTwoBodyKeplerian by using the vecnorm function.
sgp4RelativeVelocity = vecnorm(velocitySGP4 - velocityTwoBodyKeplerian,2,1);
Plot the magnitude of the relative velocity in meters per second of satSGP4 with respect to satTwoBodyKeplerian by using the plot function.
plot(time,sgp4RelativeVelocity) xlabel("Time") ylabel("Velocity deviation (m/s)") grid on
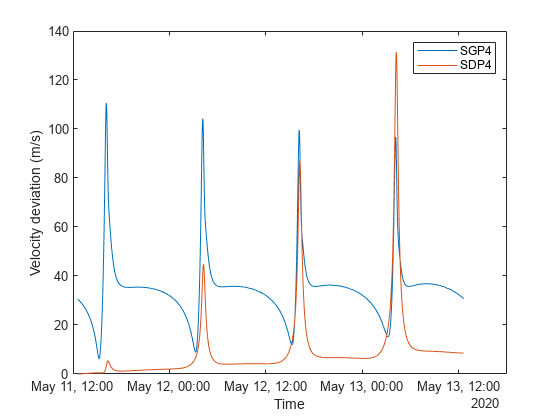
Over time, the velocity of satSDP4 deviates from that of satTwoBodyKeplerian due to the same factors that affect the position. The spikes in the graph correspond to the periapsis (the closest point in the orbit to the center of mass of the Earth), where the velocity errors become more pronounced.
The variations observed in the plots highlight the differing levels of precision offered by the two orbit propagators. The Two-Body-Keplerian orbit propagator is the less precise because it simplifies the gravitational field of the Earth as spherical and ignores all other sources of orbital perturbations. The SGP4 orbit propagator enhances the accuracy by considering the oblateness of the Earth and the effects of atmospheric drag. Given that the orbital period of the satellites in this example exceeds 225 minutes, the SGP4 orbit propagator also accounts for solar and lunar gravity.
See Also
Objects
satelliteScenario|satellite|access|groundStation|satelliteScenarioViewer|conicalSensor|transmitter|receiver
Functions
Topics
- Multi-Hop Satellite Communications Link Between Two Ground Stations
- Satellite Constellation Access to Ground Station
- Modeling Satellite Constellations Using Ephemeris Data
- Estimate GNSS Receiver Position with Simulated Satellite Constellations
- Model, Visualize, and Analyze Satellite Scenario
- Satellite Scenario Key Concepts
- Satellite Scenario Basics