La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

Modéliser et valider un système

Étape 2 sur 3 dans L'approche Model-Based Design avec Simulink

Modélisez chaque composant dans la structure du système pour représenter le comportement physique ou fonctionnel de ce composant. Vérifiez les comportements de base des composants en les simulant avec des données de test.

Ouvrir le modèle du système

Une vue d'ensemble de la structure du système est utile lors de la modélisation des composants individuels. Commencez par charger le modèle de la structure. Sur la ligne de commande MATLAB®, saisissez :

open_system('system_layout.slx')

Modéliser les composants

Un modèle Simulink^® d'un composant est basé sur plusieurs points d'initialisation :

• Une relation mathématique explicite entre la sortie et l'entrée d'un composant physique — Vous pouvez calculer les sorties du composant à partir des entrées, directement ou indirectement, via des calculs algébriques et l'intégration d'équations différentielles. Par exemple, le calcul du niveau d'eau dans un réservoir compte tenu du débit d'entrée est une relation explicite. Chaque bloc Simulink s'exécute à partir de la définition des calculs depuis ses entrées vers ses sorties.

• Une relation mathématique implicite entre les variables du modèle d'un composant physique — Comme les variables sont interdépendantes, l'affectation d'une entrée et d'une sortie au composant n'est pas simple. Par exemple, la tension à l'extrémité + d'un moteur connecté dans un circuit et la tension à l'extrémité - ont une relation implicite. Pour modéliser une telle relation dans Simulink, vous pouvez utiliser des outils de modélisation physique tels que Simscape™ ou modéliser ces variables comme faisant partie d'un composant plus important qui permet la définition des entrées et des sorties. Parfois, un examen plus approfondi des objectifs de modélisation et des définitions des composants aide à définir les relations entrée/sortie.

• Les données obtenues à partir d'un système réel — Vous avez mesuré les données d'entrée/sortie du composant réel, mais il n'existe aucune relation mathématique totalement définie. De nombreux appareils disposent de composants non modélisés qui correspondent à cette description. Par exemple, la chaleur dissipée par un téléviseur. Vous pouvez utiliser System Identification Toolbox™ pour définir la relation entrée/sortie d'un tel système.

• Une définition fonctionnelle explicite — Définissez les sorties d'un composant fonctionnel à partir des entrées via des calculs algébriques et logiques. Par exemple, la logique de commutation d'un thermostat. Vous pouvez modéliser la plupart des relations fonctionnelles sous forme de blocs et de sous-systèmes Simulink.

Ce tutoriel permet de modéliser les composants physiques et fonctionnels avec des relations entrée/sortie explicites. Dans ce tutoriel, vous allez effectuer les tâches suivantes :

1. Utilisez les équations du système pour créer un modèle Simulink.

2. Ajoutez et connectez des blocs Simulink dans l'éditeur Simulink. Les blocs représentent les coefficients et les variables des équations.

3. Créez le modèle pour chaque composant séparément. La façon la plus efficace de créer le modèle d'un système est de prendre en compte les composants de manière indépendante.

4. Commencez par créer des modèles simples à l'aide d'approximations du système. Identifiez les hypothèses qui peuvent affecter la précision de votre modèle. Ajoutez des détails de manière itérative jusqu'à ce que le niveau de complexité réponde aux exigences de modélisation et de précision.

Modéliser les composants physiques

Décrivez les relations entre les composants, par exemple le transfert de données, d'énergie et de force. Utilisez les équations du système pour créer un modèle graphique du système dans Simulink.

Voici quelques questions à vous poser avant de commencer à modéliser un composant :

• Quelles sont les constantes de chaque composant ? Quelles valeurs ne changent pas à moins qu'elles soient modifiées ?

• Quelles sont les variables de chaque composant ? Quelles valeurs changent au fil du temps ?

• Combien de variables d'état un composant possède-t-il ?

Dérivez les équations pour chaque composant en utilisant des principes scientifiques. De nombreuses équations du système se divisent en trois catégories :

• Pour les systèmes continus, les équations différentielles décrivent le taux de changement des variables et elles sont définies pour toutes les valeurs de temps. Par exemple, une équation différentielle de premier ordre donne la vitesse d'une voiture :

  $$\frac{dv(t)}{dt}=-\frac{b}{m}v(t)+u(t)$$

• Pour les systèmes discrets, les équations aux différences décrivent le taux de changement des variables, mais elles ne sont définies qu'à des moments spécifiques. Par exemple, le signal de commande d'un contrôleur proportionnel dérivé discret :

  $$pd[n]=(e[n]-e[n-1])K_d+e[n]K_p$$

• Les équations sans dérivées sont des équations algébriques. Par exemple, une équation algébrique donne le courant total dans un circuit parallèle comprenant deux composants :

  $$I_t=I_a+I_b$$

Roues et mouvement linéaire.  Deux forces agissent sur une roue :

• La force appliquée par le moteur — La force F agit dans la direction du changement de vitesse et est une entrée des sous-systèmes des roues.

• La force de traînée — La force F_drag agit contre la direction du changement de vitesse et est une fonction de la vitesse.

  $$F_{drag}=k_{drag}V\left|V\right|$$

L'accélération est proportionnelle à la somme de ces forces :

$$\begin{array}{c}(m/2)\dot{V}=F-F_{drag}\\ (m/2)\dot{V}=F-k_{drag}V\left|V\right|\\ \dot{V}=\frac{F-k_{drag}V\left|V\right|}{(m/2)}\end{array}$$

Où k_drag est le coefficient de traînée et m la masse du robot. Chaque roue porte la moitié de cette masse.

Créez le modèle de roue :

1. Dans le modèle system_layout, double-cliquez sur le sous-système Right Wheel pour afficher le sous-système vide.

2. Pour modéliser la vitesse et l'accélération, ajoutez un bloc Integrator. Laissez la condition initiale définie à 0. L'entrée de ce bloc est l'accélération Vdot et la sortie est la vitesse V.

   

3. Pour modéliser la force de traînée, ajoutez un bloc MATLAB Function de la bibliothèque User-Defined Functions. Le bloc MATLAB Function offre un moyen rapide d'implémenter des expressions mathématiques dans votre modèle. Pour modifier la fonction, double-cliquez sur le bloc pour ouvrir MATLAB Function Block Editor.

4. Dans MATLAB Function Block Editor, saisissez le code MATLAB^® pour calculer la force de traînée.

   function Fdrag=get_fdrag(V,k_drag)
   
   Fdrag=k_drag*V*abs(V);

   

5. Définissez les arguments du bloc MATLAB Function. Dans MATLAB Function Block Editor, cliquez sur « Edit Data » . Cliquez sur k_drag, définissez Scope sur Parameter, puis cliquez sur Apply.

6. Soustrayez la force de traînée de la force motrice avec le bloc Subtract. Complétez l'équation force-accélération par un bloc Gain dont le paramètre Gain est défini sur 1/(m/2).

7. Pour inverser la direction du bloc MATLAB Function, sélectionnez le bloc. Ensuite, dans Simulink Toolstrip, accédez à l'onglet Format et cliquez sur « Flip left-right » . Connectez les blocs.

   

8. La dynamique des deux roues est la même. Copiez le sous-système Right Wheel que vous venez de créer et collez-le dans le sous-système Left Wheel.

9. Pour afficher le niveau supérieur du modèle, cliquez sur « Navigate Up To Parent » .

Mouvement de rotation.   Lorsque les deux roues tournent dans des directions opposées, elles se déplacent dans un cercle de rayon r, entraînant un mouvement de rotation du robot. Lorsque les roues tournent dans la même direction, il n'y a pas de rotation. En supposant que les vitesses des roues soient toujours égales en amplitude, il est possible de modéliser le mouvement de rotation en fonction de la différence de vitesses des deux roues V_R et V_L :

$$\dot{\theta }=\frac{V_R-V_L}{2r}$$

Créez le modèle de dynamique de rotation :

1. Au niveau supérieur du modèle system_layout, double-cliquez sur le sous-système Rotation pour afficher le sous-système vide. Supprimez la connexion entre les blocs Inport et Outport.

2. Pour modéliser la vitesse et la position angulaires, ajoutez un bloc Integrator. Laissez la condition initiale définie à 0. La sortie de ce bloc est la position de rotation theta et l'entrée est la vitesse angulaire theta_dot.

3. Calculez la vitesse angulaire à partir de la vitesse tangentielle. Ajoutez un bloc Gain et définissez le paramètre Gain du bloc sur 1/(2*r).

4. Connectez les blocs.

   

5. Pour afficher le niveau supérieur du modèle, cliquez sur « Navigate Up To Parent » .

Modéliser les composants fonctionnels

Décrivez la fonction de son entrée à sa sortie. Cette description peut inclure des équations algébriques et des constructions logiques, que vous pouvez utiliser pour créer un modèle graphique du système dans Simulink.

Transformation des coordonnées.  La vitesse du robot aux coordonnées x et y, V_X et V_Y, est liée à la vitesse linéaire V_N et à l'angle theta :

$$\begin{array}{l}{V}_X=V_N\cos \left(\theta \right)\\ V_Y=V_N\sin \left(\theta \right)\end{array}$$

Créez le modèle de transformation des coordonnées :

1. Au niveau supérieur du modèle system_layout, double-cliquez sur le sous-système Coordinate Transform pour afficher le sous-système vide.

2. Pour modéliser les fonctions trigonométriques, ajoutez un bloc SinCos de la bibliothèque Math Operations.

3. Pour modéliser la multiplication, ajoutez deux blocs Product de la bibliothèque Math Operations.

4. Connectez les blocs.

   

5. Pour afficher le niveau supérieur du modèle, cliquez sur « Navigate Up To Parent » .

Définir les paramètres du modèle

Vous pouvez déterminer les valeurs appropriées des paramètres de votre modèle à l'aide de diverses sources, notamment :

• Des spécifications écrites telles que des tables de propriétés standard ou des fiches techniques de fabricant

• Des mesures directes sur un système existant

• Des estimations utilisant les entrée/sortie du système

Ce modèle utilise les paramètres suivants :

Paramètre	Symbole	Valeur
Mass	m	2.5 kg
Rolling resistance	k_drag	30 Ns2/m
Robot radius	r	0.15 m

Un modèle Simulink peut accéder aux valeurs de paramètres définies par des variables dans l'espace de travail MATLAB. Définissez ces variables en saisissant les commandes dans la fenêtre de commande MATLAB.

m = 2.5;
k_drag = 30;
r = 0.15;

Valider les composants à l'aide de la simulation

Validez les composants en fournissant une entrée et en observant la sortie. Même une validation aussi simple peut mettre en avant des moyens immédiats d'améliorer le modèle. Cet exemple valide les comportements suivants :

• Lorsqu'une force est appliquée en continu à une roue, la vitesse augmente jusqu'à ce qu'elle atteigne une vitesse en régime permanent.

• Lorsque les roues tournent dans des directions opposées, l'angle de rotation augmente à une vitesse constante.

Valider le composant de roue

Créez et exécutez un modèle de test pour le composant de roue :

1. Créez un nouveau modèle. Dans l'onglet Simulation, cliquez sur New . Copiez le bloc Subsystem nommé Right Wheel dans le nouveau modèle.

2. Pour créer une entrée de test, ajoutez un bloc Step de la bibliothèque Sources et connectez-le à l'entrée du sous-système Right Wheel. Laissez le paramètre Step time défini à 1.

3. Ajoutez un Viewer Scope à la sortie. Faites un clic droit sur le port de sortie du bloc Subsystem nommé Right Wheel et sélectionnez Create & Connect Viewer > Simulink > Scope.

   

4. Simulez le modèle. Dans l'onglet Simulation, cliquez sur Run .

   

Les résultats de la simulation indiquent que le modèle présente le comportement général attendu. Il n'y a pas de mouvement jusqu'à ce que une force soit appliquée au temps du paramètre Step time. Lorsque la force est appliquée, la vitesse commence à augmenter puis se stabilise à une constante au moment où la force appliquée et la force de traînée atteignent un équilibre. En plus de la validation, cette simulation indique la vitesse maximale de la roue pour la force donnée.

Valider le composant de rotation

Créez et exécutez un modèle de test pour le modèle de rotation :

1. Pour créer un nouveau modèle, cliquez sur « New » . Copiez le bloc Subsystem nommé Rotation dans le nouveau modèle.

2. Pour créer une entrée de test dans le nouveau modèle, ajoutez un bloc Step de la bibliothèque Sources. Laissez le paramètre Step time défini à 1. Connectez la sortie du bloc Step à l'entrée du sous-système Rotation. Cette entrée représente la différence de vitesse des roues lorsque celles-ci tournent dans des directions opposées.

3. Ajoutez un Viewer Scope à la sortie du sous-système Rotation. Faites un clic droit sur le port de sortie du sous-système et sélectionnez Create & Connect Viewer > Simulink > Scope.

   

4. Simulez le modèle. Dans l'onglet Simulation, cliquez sur Run .

   

Cette simulation montre que l'angle augmente de façon constante lorsque les roues tournent à la même vitesse dans des directions opposées. Vous pouvez améliorer le modèle pour que la sortie correspondant à l'angle soit plus facile à interpréter. Par exemple, vous pouvez :

• Convertir les unités du signal de sortie de radians en degrés en ajoutant un bloc Gain avec un gain de 180/pi.

• Afficher la valeur de sortie par cycles de 360 degrés en ajoutant un bloc Math Function avec la fonction mod.

Les fonctions trigonométriques MATLAB prennent des valeurs d'entrée en radians.

Valider le modèle

Une fois que vous avez validé les composants individuels, vous pouvez effectuer une validation similaire sur le modèle complet. Cet exemple valide les comportements suivants :

• Lorsque la même force est appliquée aux deux roues dans la même direction, le robot se déplace en ligne droite.

• Lorsque la même force est appliquée aux deux roues dans des directions opposées, le robot tourne sur place.

1. Dans le modèle system_layout, double-cliquez sur le sous-système Inputs pour afficher le sous-système vide.

2. Créez une entrée de test en ajoutant un bloc Step. Laissez le paramètre Step time défini à 1. Connectez la sortie du bloc Step aux deux blocs Outport.

   

3. Au niveau supérieur du modèle, connectez les deux signaux de sortie au même Viewer Scope.

   

4. Simulez le modèle.

   

   Dans le Viewer Scope, la ligne jaune correspond à la direction X et la ligne bleue à la direction Y. Comme l'angle est nul et ne change pas, le véhicule se déplace uniquement dans la direction X, comme prévu.

5. Double-cliquez sur le sous-système Inputs. Pour inverser la direction de la roue gauche, ajoutez un bloc Gain entre la source et la deuxième sortie et définissez le paramètre Gain sur -1.

   

6. Ajoutez un Viewer Scope à la sortie correspondant à l'angle.

7. Simulez le modèle.

Le Viewer Scope connecté aux signaux de vitesse x et y indique qu'il n'y a pas de mouvement dans le plan X-Y.

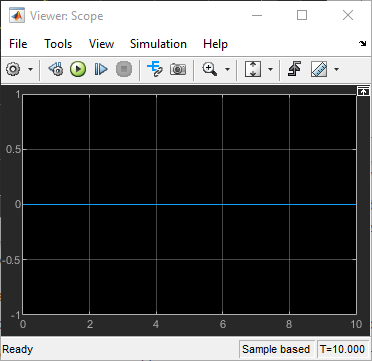
Le Viewer Scope connecté au signal d'angle indique un mouvement angulaire constant.

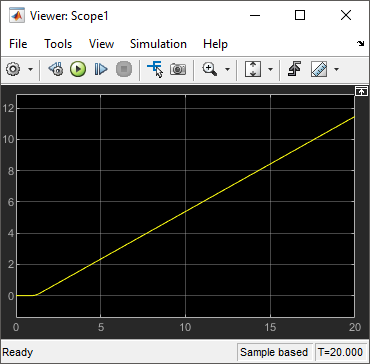
Vous pouvez utiliser ce modèle final pour répondre à de nombreuses questions sur le modèle en modifiant l'entrée.

• Que se passe-t-il lorsque l'angle initial n'est pas nul ?

• Combien de temps faut-il pour que le mouvement s'arrête lorsque la force devient nulle ?

• Que se passe-t-il lorsque le robot est plus lourd ?

• Que se passe-t-il lorsque le robot se déplace sur une surface plus lisse avec un coefficient de traînée inférieur ?

Sujets associés

• Définition et structure du système
• Concevoir un système dans Simulink

L'approche Model-Based Design avec Simulink

Suivant