linearizeOptions
Set linearization options
Description
The LinearizeOptions object stores and manages the options for
linearization.
Creation
Description
options = linearizeOptions
options = linearizeOptions(PropertyName=Value)
Properties
General Options
Algorithm used for linearization, specified as one of the following:
'blockbyblock'— Individually linearize each block in the model, and combine the results to produce the linearization of the specified system.'numericalpert'— Full-model numerical-perturbation linearization in which root-level inports and states are perturbed using forward differences; that is, by adding perturbations to the input and state values. This perturbation method is typically faster than the'numericalpert2'method.'numericalpert2'— Full-model numerical-perturbation linearization in which root-level inports and states are numerically perturbed using central differences; that is, by perturbing the input and state values in both positive and negative directions. This perturbation method is typically more accurate than the'numericalpert'method.
The numerical perturbation linearization methods ignore linear analysis points set in the model and use root-level inports and outports instead.
Block-by-block linearization has several advantages over full-model numerical perturbation:
Many Simulink® blocks have a preprogrammed exact linearization.
You can use linear analysis points to specify a portion of the model to linearize.
You can configure blocks to use custom linearizations without affecting your model simulation.
Structurally nonminimal states are automatically removed.
You can specify linearizations that include uncertainty (requires Robust Control Toolbox™ software).
You can obtain detailed diagnostic information about the linearization.
Sample time of linearization result, specified as one of the following:
-1— Set the sample time to the least common multiple of the nonzero sample times in the model.0— Create a continuous-time model.Positive scalar — Specify the sample time for discrete-time systems.
Flag indicating whether to truncate names of I/Os and states
in the linearized model, specified as the comma-separated pair consisting
of 'UseFullBlockNameLabels' and either:
"off",0, orfalse— Use truncated names for the I/Os and states in the linearized model."on",1, ortrue— Use the full block path to name the I/Os and states in the linearized model.
Flag indicating whether to use bus signal channel numbers or
names to label the I/Os in the linearized model, specified as the
comma-separated pair consisting of 'UseBusSignalLabels' and
one of the following:
"off",0, orfalse— Use bus signal channel numbers to label I/Os on bus signals in the linearized model."on",1, ortrue— Use bus signal names to label I/Os on bus signals in the linearized model. Bus signal names appear in the results when the I/O points are located at the output of the following blocks:Root-level inport block containing a bus object
Bus creator block
Subsystem block whose source traces back to the output of a bus creator block
Subsystem block whose source traces back to a root-level inport by passing through only virtual or nonvirtual subsystem boundaries
Flag indicating whether to compute linearization offsets for inputs, outputs, states, and state derivatives or updated states, specified as one of the following:
"none"— Do not compute linearization offsets."stuct"— Return computed linearization offsets in theinfooutput argument oflinearize."system"— Store computed linearization offsets in theOffsetsproperty of the linearized systemsys. This option is applicable only whensysis anssorsparssmodel.
For an example, see Batch Linearize Plant Model and Obtain Linearization Offsets.
You can configure an LPV System block using linearization offsets. For an example, see Approximate Nonlinear Behavior Using Array of LTI Systems
Block-By-Block Algorithm
Flag indicating whether to omit blocks that are not in the linearization path,
specified as the comma-separated pair consisting of
'BlockReduction' and one of the following:
"on",1, ortrue— Return a linearized model that does not include states from noncontributing linearization paths."off",0, orfalse— Return a linearized model that includes all the states of the model.
Dead linearization paths can include:
Blocks that linearize to zero.
Switch blocks that are not active along the path.
Disabled subsystems.
Signals marked as open-loop linearization points.
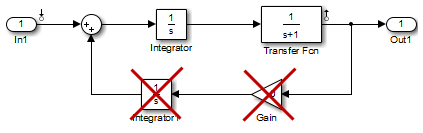
For example, if this flag set to 'on', the linearization result
of the model shown in the following figure includes only two states. It does not
include states from the two blocks outside the linearization path. These states do not
appear because these blocks are on a dead linearization path with a block that
linearizes to zero (the zero gain block).
This option applies only when LinearizationAlgorithm is
'blockbyblock'. BlockReduction is always
treated as 'on' when LinearizationAlgorithm is
'numericalpert' or 'numericalpert2'.
Since R2025a
Flag indicating whether to perform state-consistent reduction for linearized array with uniform state dimension. This means that the software removes only the states and delays that do not contribute to the input-output map for all models in the batch linearization array.
Specify this option as one of these logical on/off values:
"on",1, ortrue— Perform state-consistent reduction."off",0, orfalse— Do not perform state-consistent reduction.
For an example, see Obtain Batch Linearization Results with Uniform State Consistency.
Flag indicating whether to remove discrete-time states from the linearization,
specified as the comma-separated pair consisting of
'IgnoreDiscreteStates' and one of the following:
"off",0, orfalse— Always include discrete-time states."on",1, ortrue— Remove discrete states from the linearization. Use this option when performing continuous-time linearization (SampleTime = 0) to accept theDvalue for all blocks with discrete-time states.
This option applies only when LinearizationAlgorithm is
'blockbyblock'.
Flag indicating whether to compute linearization with exact delays, specified as
the comma-separated pair consisting of 'UseExactDelayModel' and one
of the following:
"off",0, orfalse— Return a linear model with approximate delays."on",1, ortrue— Return a linear model with exact delays.
This option applies only when LinearizationAlgorithm is
'blockbyblock'.
Flag indicating whether to recompile the model when varying parameter values for
linearization, specified as the comma-separated pair consisting of
'AreParamsTunable' and one of the following:
"on",1, ortrue— Do not recompile the model when all varying parameters are tunable. If any varying parameters are not tunable, recompile the model for each parameter grid point, and issue a warning message."off",0, orfalse— Recompile the model for each parameter grid point. Use this option when you vary the values of nontunable parameters.
For more information about model compilation when you linearize with parameter variation, see Batch Linearization Efficiency When You Vary Parameter Values.
Flag indicating whether to store diagnostic information during linearization, specified as the comma-separated pair consisting of 'StoreAdvisor' and one of the following:
"off",0, orfalse— Do not store linearization diagnostic information."on",1, ortrue— Store linearization diagnostic information.
Linearization commands store and return diagnostic information in a LinearizationAdvisor object. For an example of troubleshooting
linearization results using a LinearizationAdvisor object, see Troubleshoot Linearization Results at Command Line.
Numerical Perturbation Algorithm
Numerical perturbation level, specified as the comma-separated pair consisting of
'NumericalPertRel' and a positive scalar. This option applies
only when LinearizationAlgorithm is
'numericalpert' or 'numericalpert2'.
The perturbation levels for the system states are:
The perturbation levels for the system inputs are:
You can override these values using the NumericalXPert or
NumericalUPert options.
State perturbation levels, specified as the comma-separated pair consisting of
'NumericalXPert' and an operating point object. This option
applies only when LinearizationAlgorithm is
'numericalpert' or 'numericalpert2'.
To set individual perturbation levels for each state:
Create an operating point object for the model using the
operpointcommand.xPert = operpoint('watertank');Set the state values in the operating point object to the perturbation levels.
xPert.States(1).x = 2e-3; xPert.States(2).x = 3e-3;
Set the value of the
NumericalXPertoption to the operating point object.opt = linearizeOptions('LinearizationAlgorithm','numericalpert'); opt.NumericalXPert = xPert;
If NumericalXPert is empty, [], the
linearization algorithm derives the state perturbation levels using
NumericalPertRel.
Input perturbation levels, specified as the comma-separated pair consisting of
'NumericalUPert' and an operating point object. This option
applies only when LinearizationAlgorithm is
'numericalpert' or 'numericalpert2'.
To set individual perturbation levels for each input:
Create an operating point object for the model using the
operpointcommand.uPert = operpoint('watertank');Set the input values in the operating point object to the perturbation levels.
uPert.Inputs(1).x = 3e-3;
Set the value of the
NumericalUPertoption to the operating point object.opt = linearizeOptions('LinearizationAlgorithm','numericalpert'); opt.NumericalUPert = uPert;
If NumericalUPert is empty, [], the
linearization algorithm derives the input perturbation levels using
NumericalPertRel.
Rate Conversion
Rate conversion options, specified as a RateConversionOptions
object with the following properties.
Method used for rate conversion when
linearizing a multirate system, specified as the comma-separated pair consisting
of 'RateConversionMethod' and one of the following:
'zoh'— Zero-order hold rate conversion method'tustin'— Tustin (bilinear) method'prewarp'— Tustin method with frequency prewarp. When you use this method, set thePrewarpFrequencyoption to the desired prewarp frequency.'upsampling_zoh'— Upsample discrete states when possible, and use'zoh'otherwise.'upsampling_tustin'— Upsample discrete states when possible, and use'tustin'otherwise.'upsampling_prewarp'— Upsample discrete states when possible, and use'prewarp'otherwise. When you use this method, set thePrewarpFrequencyoption to the desired prewarp frequency.
For more information on rate conversion and linearization of multirate models, see:
Note
If you use a rate conversion method other than 'zoh',
the converted states no longer have the same physical meaning as the
original states. As a result, the state names in the resulting LTI system
change to '?'.
This option applies only when LinearizationAlgorithm is
'blockbyblock'.
Example: options.RateConversionOptions.Method =
"tustin";
Since R2025a
Format of modeling extra delays arising from discretization, specified as
'delay' or 'state'. Discretizing models
with input or output delays that are fractional multiples of
Ts can give rise to additional delays besides the discrete
input and output delays. Use this option to specify whether to model these extra
delays as internal delays (''delay') or additional states
('state').
For an example, see Model Fractional Delays During Discretization.
This option is only applicable when UseExactDelayModel
is on, or when substituting blocks with models that have delays.
Example: options.RateConversionOptions.DelayModeling =
"delay";
Prewarp frequency in rad/s, specified as a nonnegative scalar. This option
applies only when RateConversionMethod is either
'prewarp' or
'upsampling_prewarp'.
Example: options.RateConversionOptions.PrewarpFrequency =
100;
Since R2025a
Maximum order of the Thiran filter used to approximate fractional delays in
the 'tustin' method. A value of 0 means that discretization
rounds fractional delays to the nearest integer multiple of the sample time. If
you set this property to a positive integer, discretization uses thiran to approximate fractional
delays before discretizing.
For models with fractional delays, the Thiran filters contribute additional
internal delays when DelayModeling is set to
'delay' and additional states when
DelayModeling is set to 'state'.
For an example, see Model Fractional Delays During Discretization.
This option is only applicable when UseExactDelayModel
is on, or when substituting blocks with models that have delays.
Example: options.RateConversionOptions.ThiranOrder =
5;
Object Functions
linearize | Linear approximation of Simulink model or subsystem |
slLinearizer | Interface for batch linearization of Simulink models |
ulinearize (Robust Control Toolbox) | Linearize Simulink model with Uncertain State Space block |
Examples
Create a linearization option set that stores the linearization offsets with the linearized model and instructs linearization not to omit blocks outside the linearization path.
options = linearizeOptions(BlockReduction='off', StoreOffsets='system')
options =
LinearizeOptions with properties:
LinearizationAlgorithm: 'blockbyblock'
SampleTime: -1
UseFullBlockNameLabels: off
UseBusSignalLabels: off
StoreOffsets: 'system'
Block-by-block algorithm options
BlockReduction: off
BatchConsistency: off
IgnoreDiscreteStates: off
UseExactDelayModel: off
AreParamsTunable: on
StoreAdvisor: off
Numerical perturbation algorithm options
NumericalPertRel: 1.0000e-05
NumericalXPert: []
NumericalUPert: []
Rate conversion options (RateConversionOptions)
Method: 'zoh'
DelayModeling: 'state'
PrewarpFrequency: 10
ThiranOrder: 0
Additionally, to set the rate conversion method to the Tustin method with prewarping at a frequency of 10 rad/s, use dot notation to set the values of options.
options.RateConversionOptions.Method = 'prewarp';
options.RateConversionOptions.PrewarpFrequency = 10options =
LinearizeOptions with properties:
LinearizationAlgorithm: 'blockbyblock'
SampleTime: -1
UseFullBlockNameLabels: off
UseBusSignalLabels: off
StoreOffsets: 'system'
Block-by-block algorithm options
BlockReduction: off
BatchConsistency: off
IgnoreDiscreteStates: off
UseExactDelayModel: off
AreParamsTunable: on
StoreAdvisor: off
Numerical perturbation algorithm options
NumericalPertRel: 1.0000e-05
NumericalXPert: []
NumericalUPert: []
Rate conversion options (RateConversionOptions)
Method: 'prewarp'
DelayModeling: 'state'
PrewarpFrequency: 10
ThiranOrder: 0
Version History
Introduced in R2013bThe linearization tools available in Simulink Control Design™ software now provide the following enhancements for linearization:
Sparse linearization — The software can now return a first-order sparse (
sparss) model without relying on block substitution for sparse-capable blocks. Previously, you could only perform sparse linearization whenBlockReductionoption oflinearizeOptionsandslTunerOptionswas set to"on".Enhanced rate conversion options — The
linearizeOptionsandslTunerOptionsobjects now store the rate conversion related options under the newRateConversionOptionsproperty. Additionally, rate conversion options now includeDelayModelingandThiranOrder. TheDelayModelingoption allows you to specify whether to model extra delays from discretization as internal delays or additional states. TheThiranOrderoption specifies the order of the Thiran filter used to approximate fractional delays in the Tustin discretization. To set these properties, use dot notation:opt = linearizeOptions; opt.RateConversionOptions.Method = "tustin"; opt.RateConversionOptions.DelayModeling = "delay"; opt.RateConversionOptions.ThiranOrder = 3;
Offset computation and storage — The software now allows you to directly store offsets in the
Offsetsproperty of the linearizedssandsparssmodels using the new value"system"for the option.opt = linearizeOptions(StoreOffsets="system")Additionally, you can now compute offsets during snapshot linearization. Calculation of offsets during simulation are limited to continuous time blocks and linear discrete time blocks. For example:
tsnap = 7.5; sys = linearize(mdl,io,tsnap,opt);
Consistent block reduction — When performing batch linearization, you can now use the new
BatchConsistencyoption oflinearizeOptionsandslTunerOptionsto only reduce the states that are reducible for all models in the grid of operating points. In addition, the software maintains this consistency during any rate conversion or delay modeling.
These changes also simplify LPV modeling workflows. Building LPV models in MATLAB® and Simulink require consistent and uniform state dimensions, delay modeling, and offset
handling across the linearization grid. For more information about building LPV models from
batch linearization results, see ssInterpolant.
As a result of improvements to linearization workflows, how you specify options related
to offsets and rate conversion in linearizeOptions and
slTunerOptions have changed. This table describes the change in the
workflow.
| Before R2025a | R2025a |
|---|---|
|
Offsets
|
Offsets
|
|
Rate conversion
|
Rate conversion
|
See Also
linearize | slLinearizer | ulinearize (Robust Control Toolbox) | linlft
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)