Quasi-Static Analysis of a Robotic Arm in MATLAB
This example demonstrates a workflow for dynamics analysis of a robotic arm in MATLAB® using Simscape™ Multibody™. It demonstrates various classes under simscape.multibody.* namespace to build and analyze a multibody system in MATLAB.
The example shows how to:
Build a robotic system programmatically.
Generate a user-defined end-effector trajectory.
Solve inverse kinematics involving joint limits via optimization to find joint positions at each step.
Use a root-finding approach to compute the maximum lifting force such that at least one joint actuator reaches its torque limit.
All joints are set to zero velocity and zero acceleration. This represents a quasi-static scenario where the manipulator is effectively paused in each pose. In other mode, no inertial or dynamic effects (like momentum or Coriolis forces) are considered. Instead, each pose is treated as a static equilibrium that balances the external load and internal link geometry to determine joint torques.
Build a Robotic Arm
Build a serial-link manipulator. The buildSerialLinkManipulator function constructs a Multibody model in the workspace, which is then compiled to obtain a CompiledMultibody (cmb):
% To simplify the process and avoid repeatedly typing the namespace name % for the classes, you can use the import function. import simscape.Value simscape.op.* simscape.multibody.*; addpath(fullfile('QuasiStaticAnalysisOfARoboticArmInMATLABSupport','Scripts')); mb = buildSerialLinkManipulator; cmb = compile(mb);
Generate an End-Effector Trajectory
Define a smooth arc from a start position to an end position for the end-effector of the robotic arm. The arc should reach its maximum height in the z-axis at the midpoint:
numIterations = 25; % Number of discrete points along the trajectory startPos = [0.5, 0, 0]; % [x, y, z] start endPos = [0, 0.5, 0]; % [x, y, z] end zPeak = 0.5; % Maximum z-height at the arc midpoint s = linspace(0, 1, numIterations); % Parameter s in [0..1], for numIterations points tVals = 3*s.^2 - 2*s.^3; % Smooth step function t(s) = 3s^2 - 2s^3 % Compute X & Y via linear interpolation between start and end x = startPos(1) + (endPos(1) - startPos(1)).*tVals; y = startPos(2) + (endPos(2) - startPos(2)).*tVals; % Sine bump in Z from 0 up to zPeak, back to 0 z = zPeak .* sin(pi .* tVals);
Generate States via Inverse Kinematics
To analyze the robot's dynamics for each point on the trajectory, we need the specific joint angles that place the end-effector at (x, y, z). This is solved via fmincon, imposing joint angle limits. The four key joints under consideration are:
"Arm_Subsys/Rev_1/Rz"
"Arm_Subsys/Rev_2/Rz"
"Arm_Subsys/Rev_3/Rz"
"Arm_Subsys/Rev_4/Rz"
The joint angular velocitites are set to zero at each pose so that the focus is on the static torque required to hold the payload (no inertial effects):
jointAngles = zeros(numIterations,4); % Preallocate a matrix of joint positions for each orientation of interest states = repmat(State,1,numIterations); % Preallocate a vector of state objects initial_guess = [0; 0; 0; 0]; % Starting guess for the optimization % Loop over end-effector orientations for i = 1:numIterations target_translation = [x(i); y(i); z(i)]; % Target end-effector position % Optimization objective: minimize the transformation error between the % actual end-effector position and target_translation. objective_function = @(q) computeTargetEndEffectorPosError(cmb,q,target_translation); % Perform optimization to find the joint angles. Here, "sqp" is selected for its robustness in handling nonlinear % constraints and for typically converging quickly on smaller problems. options = optimoptions("fmincon","Display","none","Algorithm","sqp"); % Joint limits justification: % - The bottom swivel (joint 1) can rotate a full 360°, so it is set to (-inf, inf). % - The next joint (joint 2) pivots from 0° (horizontal) to 90° (vertical). % - The final two joints (3 and 4) can each rotate from -90° to +90° near the tip. q_opt = fmincon(objective_function, ... initial_guess, ... [],[],[],[], ... [-inf; 0; -90; -90], ... % lower bounds (deg) [ inf; 90; 90; 90], ... % upper bounds (deg) [],options); % Update the guess for the next iteration, to have smooth transition % between two steps. initial_guess = q_opt; jointAngles(i,:) = q_opt; % Create an OperatingPoint to define joint positions and zero velocity op = simscape.op.OperatingPoint; op("Arm_Subsys/Rev_1/Rz/q") = Target(jointAngles(i, 1),"deg","High"); op("Arm_Subsys/Rev_2/Rz/q") = Target(jointAngles(i, 2),"deg","High"); op("Arm_Subsys/Rev_3/Rz/q") = Target(jointAngles(i, 3),"deg","High"); op("Arm_Subsys/Rev_4/Rz/q") = Target(jointAngles(i, 4),"deg","High"); op("Arm_Subsys/Rev_1/Rz/w") = Target(0,"deg/s","High"); op("Arm_Subsys/Rev_2/Rz/w") = Target(0,"deg/s","High"); op("Arm_Subsys/Rev_3/Rz/w") = Target(0,"deg/s","High"); op("Arm_Subsys/Rev_4/Rz/w") = Target(0,"deg/s","High"); % Compute and store the system state states(i) = computeState(cmb,op); % Visualize the manipulator for each iteration visualize(cmb,states(i),"robotTrajectory"); end
Perform Dynamics Analysis
Next, determine the maximum lifting force in the -Z direction such that at least one joint reaches its torque limit:
% The motor at each revolute primitive would have a maximum torque capacity. torqueLimits = [20, 15, 10, 5]; % The torque limit (in N*m) decreases moving from base to tip % Set up Computed Torque actDict = JointActuationDictionary; compT = RevolutePrimitiveActuationTorque("Computed"); actDict("Arm_Subsys/Rev_1/Rz") = compT; actDict("Arm_Subsys/Rev_2/Rz") = compT; actDict("Arm_Subsys/Rev_3/Rz") = compT; actDict("Arm_Subsys/Rev_4/Rz") = compT; % Zero Joint Acceleration accelDict = JointAccelerationDictionary; zeroAccel = RevolutePrimitiveAcceleration(Value(0,"deg/s^2")); accelDict("Arm_Subsys/Rev_1/Rz") = zeroAccel; accelDict("Arm_Subsys/Rev_2/Rz") = zeroAccel; accelDict("Arm_Subsys/Rev_3/Rz") = zeroAccel; accelDict("Arm_Subsys/Rev_4/Rz") = zeroAccel; % Define a handle for the root finder: ratioGuess(f) = maxRatio - 1, where % ratio is torque/torqueLimit. % getMaxTorqueRatioForAllStates applies the specified force at the end effector and % compute the resulting torques for each joint/state, using computeDynamics. % It returns the maximum absolute torque and the complete torque matrix. ratioGuess = @(testF) (getMaxTorqueRatioForAllStates(testF, cmb, states, actDict, accelDict, torqueLimits)) - 1; % Bracket the guess between lowF and highF, so fzero can locate a root where % ratioGuess(f) = 0 (i.e., the joint torque ratio hits 1). % The function must have opposite signs at these endpoints, lowF = 0; highF = 500; valLow = ratioGuess(lowF); % if <0 => under limit valHigh = ratioGuess(highF); % if >0 => over limit % Solve ratioGuess(f)=0 => means maxRatio=1 => at least one joint is exactly at limit f_solution = fzero(ratioGuess,[lowF, highF]); % Retrieve the torque distribution at that force [finalRatio, torqueMatrix] = getMaxTorqueRatioForAllStates( ... f_solution, cmb, states, actDict, accelDict, torqueLimits); % Now find max force for each orientation, the overall maximum lifting % capacity will be minimum of all. maxForces = zeros(numIterations,1); for (i = 1:numIterations) ratioGuess_single = @(testF) getMaxTorqueRatioForOneState(... testF,cmb,states(i),actDict,accelDict,torqueLimits) - 1; maxForces(i) = fzero(ratioGuess_single, [lowF, highF]); end
Plot the Results
Retrieve the final poses of each link in 3-D and overlay the manipulator's geometry at key frames along the trajectory, plus the path of the end-effector. We also produce a 2-D plot of the four joint torques vs iteration index:
trajectory = zeros(numIterations,3); % Store end-effector positions for plotting figure('Color','w','Units','pixels','Position',[100 100 1200 800]); title('Lifting Capacity Along the Robotic Arm Trajectory','FontSize',20); hold on; grid on; view(3); axis equal; xlabel('X'); ylabel('Y'); zlabel('Z'); % Some basic lighting camlight headlight; lighting gouraud; material dull; % Choose certain key frames to display the arm keyFrames = [1 5 10 15 20 25]; for iter = 1:numIterations % Plot in MATLAB link_1_neg = transformation(cmb,"World/W","Arm_Subsys/arm_link_1/NegEnd",states(iter)).Translation.Offset.value; link_1_pos = transformation(cmb,"World/W","Arm_Subsys/arm_link_1/PosEnd",states(iter)).Translation.Offset.value; link_2_neg = transformation(cmb,"World/W","Arm_Subsys/arm_link_2/NegEnd",states(iter)).Translation.Offset.value; link_2_pos = transformation(cmb,"World/W","Arm_Subsys/arm_link_2/PosEnd",states(iter)).Translation.Offset.value; link_3_neg = transformation(cmb,"World/W","Arm_Subsys/arm_link_3/NegEnd",states(iter)).Translation.Offset.value; link_3_pos = transformation(cmb,"World/W","Arm_Subsys/arm_link_3/PosEnd",states(iter)).Translation.Offset.value; % Plot only certain frames to reduce clutter if (ismember(iter, keyFrames)) plotRoboticArm(link_1_neg,link_1_pos, ... link_2_neg,link_2_pos, ... link_3_neg,link_3_pos, ... maxForces(iter)); end % Store the end-effector position trajectory(iter, :) = link_3_pos'; end % Highlight the Max Lifting Force on the Plot text(0.02, 0.95, 0.02, ... sprintf('Overall Max Lifting Capacity : %.2f N',f_solution), ... 'Units','normalized', ... 'FontSize',12, ... 'FontWeight','bold', ... 'Color','magenta'); % Plot the path of the end-effector plot3(trajectory(:, 1),trajectory(:, 2),trajectory(:, 3),'k--','LineWidth',1.5); hold off;
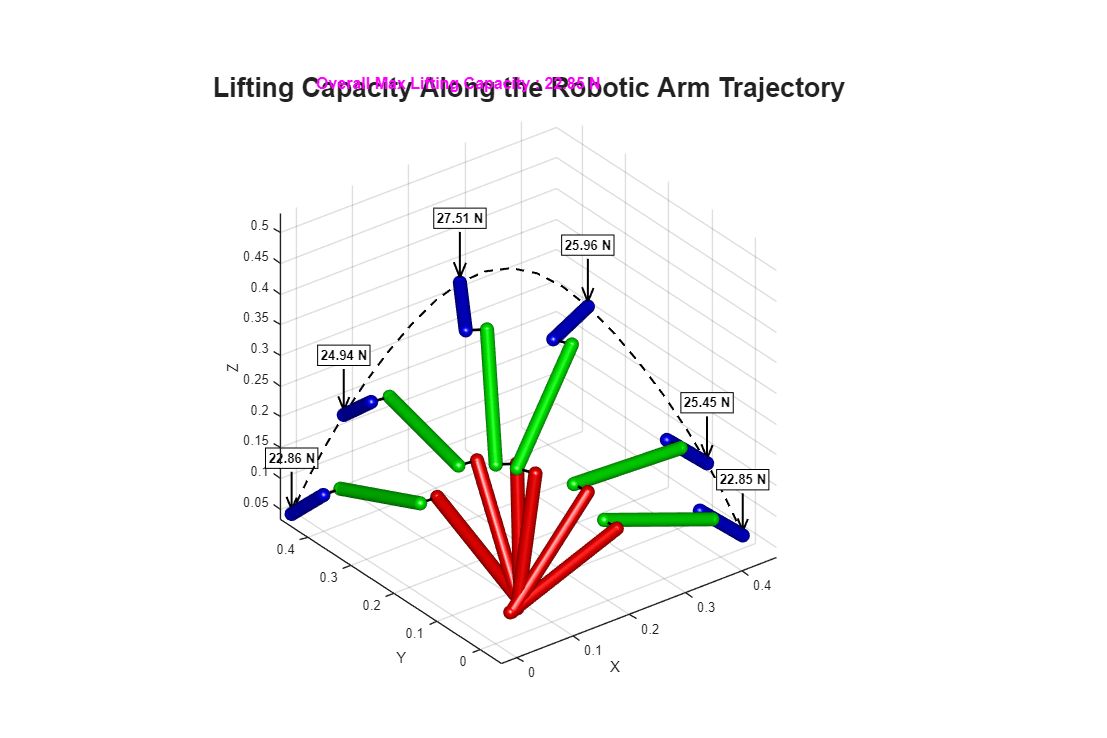
% Finally, plot the torque profiles for each of the 4 joint primitives
plotTorques(torqueMatrix);[Torque1] Max torque=0.00 Nm at iteration 9 [Torque2] Max torque=15.00 Nm at iteration 1 [Torque3] Max torque=9.50 Nm at iteration 18 [Torque4] Max torque=4.30 Nm at iteration 10
![Figure contains an axes object. The axes object with title Joint Torques Over Trajectory, xlabel Iteration Index, ylabel Torque [N·m] contains 12 objects of type line, text. One or more of the lines displays its values using only markers These objects represent Torque1, Torque2, Torque3, Torque4.](../../examples/sm/win64/QuasiStaticAnalysisOfARoboticArmInMATLABExample_02.png)
rmpath(fullfile('QuasiStaticAnalysisOfARoboticArmInMATLABSupport','Scripts'));