Filters
Use these examples to learn how to design signal processing filters to remove or enhance frequency components.
Featured Examples
Analog Anti-Aliasing Filter
An analog implementation of an anti-aliasing filter for use with an A-to-D converter. The filter cut-off frequency is set to 500Hz in order to match the A-to-D converter sampling frequency of 1kHz. The test signal incorporates a desired 50Hz sinusoid plus a higher frequency component at 1100Hz that cannot be captured with a 1kHz A-to-D sampling frequency. The scope shows the captured signal without and with anti-aliasing. With the anti-alias filter the 50Hz sine wave amplitude is correctly measured with an amplitude of 1 and corresponding power of 0.5W, i.e., 27dBm for a 1ohm reference load.
Band-Pass Filter Using Three Mutually-Coupled Inductors
An implementation of a band-pass filter using three mutually-coupled inductors. The model can be used to validate filter parameters which are chosen to provide a band-pass centered on 100MHz. A band-limited noise source is up-shifted by a 100MHz oscillator and applied to the filter. The response is then down-shifted by the oscillator. The model StopFcn callback takes FFTs of the source and response and estimates the filter frequency response.
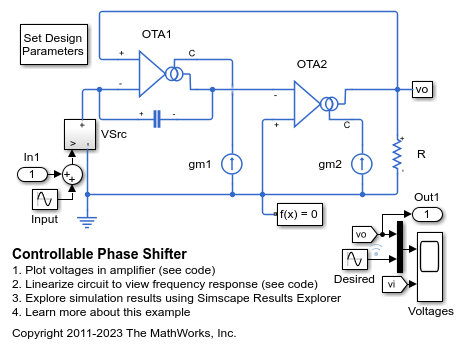
Controllable Phase Shifter
An implementation of a first order phase shifting filter. The filter is characterized by the transfer function H(s) = (sC - gm1)/(sC + gm1). Double-click on the Set Design Parameters block to set the desired phase shift, amplitude of the input signal, and the frequency of the input signal. The block mask calls a function which sets the parameter values in the model workspace.
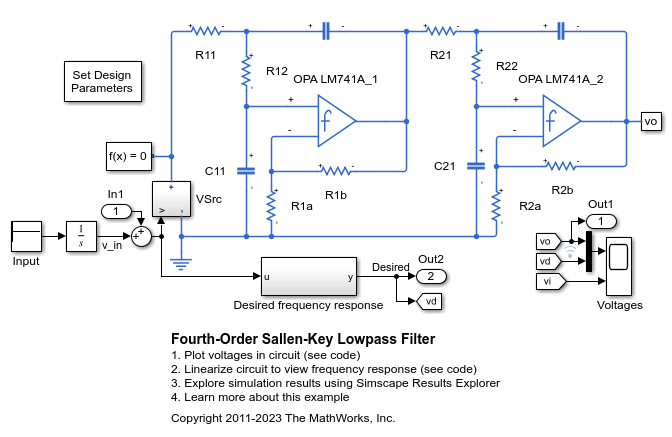
Fourth-Order Sallen-Key Lowpass Filter
An implementation of a fourth-order Sallen-Key low-pass filter using Operational Amplifiers (OPAs). The filter design parameters, cut-off frequency (f1) and DC gain (K), are specified by double-clicking on the Set Design Parameters block. Pass-band ripple is predefined to be 1dB using a Chebyshev response. The block mask calls a function which sets the parameter values in the model workspace.
Low-Pass Filter Using Operational Transconductance Amplifiers
Model a second-order active low-pass filter. The filter is characterized by the transfer function H(s) = 1 / ( (s/w1)^2 + (1/Q)*(s/w1) + 1 ) where w1 = 2*pi*f1, f1 is the cut-off frequency and Q is the quality factor. Double-click on the Set Design Parameters block to set parameters f1 and Q. The block mask calls a function which sets the parameter values in the model workspace.
