profileLikelihood
Syntax
Description
[___] = profileLikelihood(
specifies additional options using one or more name-value arguments. For example, you can
specify the significance level for the confidence interval and the values for the
coefficient of interest. mdl,coef,Name=Value)
Examples
Load a table of standardized variables generated from the carbig data set.
load standardizedcar.matThe table tbl contains the variables Horsepower, Weight, and MPG, which represent car horsepower, weight, and miles per gallon, respectively.
Fit a nonlinear model to the data using Horsepower and Weight as predictors, and MPG as the response.
modelfun = @(b,x) exp(b(1)*x(:,1))+b(2)*x(:,2)+b(3); beta0 = [1 1 1]; mdl = fitnlm(tbl,modelfun,beta0)
mdl =
Nonlinear regression model:
MPG ~ exp(b1*Horsepower) + b2*Weight + b3
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ _______ ___________
b1 -0.57016 0.045819 -12.444 3.7325e-30
b2 -0.39274 0.043737 -8.9797 1.1804e-17
b3 -1.1417 0.034104 -33.476 1.3291e-116
Number of observations: 392, Error degrees of freedom: 389
Root Mean Squared Error: 0.516
R-Squared: 0.735, Adjusted R-Squared 0.733
F-statistic vs. constant model: 539, p-value = 8.27e-113
mdl contains a fitted nonlinear regression model. The coefficient b1 is a nonlinear coefficient because it is inside the exponential term in the model function.
Calculate the profile loglikelihood and confidence interval for b1.
[LV,PV,CI] = profileLikelihood(mdl,"b1");
CICI = 1×2
-0.6597 -0.4660
The output shows the 95% likelihood-ratio confidence interval for b1.
Plot the profile loglikelihood values for b1 using the plotProfileLikelihood function.
plotProfileLikelihood(mdl,"b1")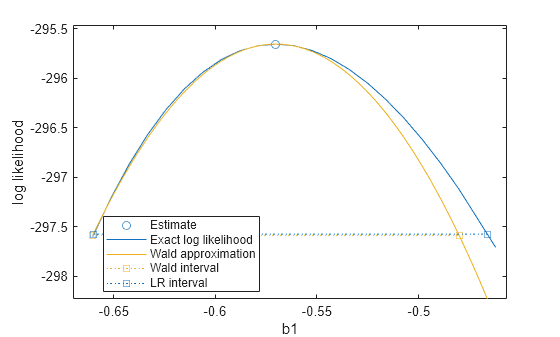
The plot shows the loglikelihood values together with the estimated value for b1, the Wald approximation, and the Wald and likelihood-ratio confidence intervals. The calculated values for b1 cover the confidence intervals, and the maximum likelihood estimate for b1 appears at the peak of the profile loglikelihood, confirming it is the maximum likelihood estimate. The likelihood-ratio confidence interval is slightly wider than the Wald interval, and is also asymmetric. However, the closeness of the two intervals suggests that the assumptions of the Wald approximation hold true for this model.
Load the reaction data set.
load reactionThe variables reactants and rate contain data for the partial pressures of three chemicals and their reactant rates. The vector beta contains initial values for the Hougen-Watson model coefficients.
Fit the Hougen-Watson model to the data using the hougen function. Use reactants as the predictor data and rate as the response.
mdl = fitnlm(reactants,rate,@hougen,beta)
mdl =
Nonlinear regression model:
y ~ hougen(b,X)
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ _______
b1 1.2526 0.86701 1.4447 0.18654
b2 0.062776 0.043561 1.4411 0.18753
b3 0.040048 0.030885 1.2967 0.23089
b4 0.11242 0.075157 1.4957 0.17309
b5 1.1914 0.83671 1.4239 0.1923
Number of observations: 13, Error degrees of freedom: 8
Root Mean Squared Error: 0.193
R-Squared: 0.999, Adjusted R-Squared 0.998
F-statistic vs. zero model: 3.91e+03, p-value = 2.54e-13
mdl contains the fitted nonlinear regression model. The estimate for b2 is near 0.06 and has a large p-value.
Calculate the profile loglikelihood for b2 in an interval around its estimated value. Plot the loglikelihood values against the specified values for b2.
[LV2,PV2] = profileLikelihood(mdl,"b2",CoefficientValues=[0.01:0.01:1]); plot(PV2,LV2) xlabel("b2") ylabel("loglikelihood")
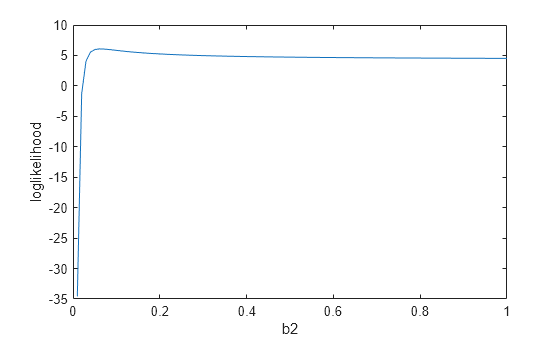
The profile loglikelihood has a nonlinear elbow shape and does not change significantly for values of b2 larger than 0.1. This result is consistent with the large p-value, which suggests that b2 does not have a statistically significant effect on the response variable.
Input Arguments
Nonlinear regression model, specified as a NonLinearModel object created using fitnlm.
Coefficient of interest, specified as a string, character array, or index. Coefficients not
specified in coef are called nuisance coefficients. For each value
of the coefficient of interest, profileLikelihood calculates values for
the nuisance coefficients. For more information, see Profile Loglikelihood.
Example: "b1"
Example: 3
Data Types: single | double | char | string
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: [LV,PV,CI]=profileLikelihood(mdl,"b2",Alpha=0.01,Scale="log")
calculates the 99% confidence intervals and values for the coefficient of interest on the
log scale.
Significance level for the confidence intervals, specified as a numeric value in the range [0,1]. The confidence level of CI is equal to 100(1 – alpha)%. Alpha is the probability that the confidence interval does not contain the true value.
Example: Alpha=0.01
Data Types: single | double
Values for the coefficient of interest, specified as a numeric scalar or vector. When you do
not specify CoefficientValues,
profileLikelihood selects values for
coef that cover a typical
confidence interval.
Example: CoefficientValues=[0:0.02:1]
Data Types: single | double
Scale for plotting the loglikelihood values, specified as
"linear" or "log".
When
Scaleis"linear", the function selects values for the coefficient of interest that lie on a Euclidean grid.When
Scaleis"log", the function selects values for the coefficient of interest that lie on a logarithmic grid. You can specifyScaleas"log"only for positive coefficients.
Example: Scale="log"
Data Types: string | char
Output Arguments
Loglikelihood values, returned as a numeric scalar or vector.
Values for the coefficient of interest, returned as a numeric scalar or vector. You
can specify PV using the CoefficientValues
name-value argument. When you do not specify CoefficientValues,
profileLikelihood returns values for PV that cover
a typical confidence interval.
Confidence interval for the coefficient of interest, returned as a 1-by-2 numeric
vector. CI is a likelihood-ratio confidence interval, which
profileLikelihood calculates by determining the coefficient values for
which the profile likelihood drops below a threshold.
Data Types: single | double
More About
The profile loglikelihood describes the maximum possible likelihood for a set of nuisance coefficients, given a fixed value of the coefficient of interest. The coefficient of interest is a coefficient that you want to vary, and the nuisance coefficients are the other coefficients in the model formula.
The profile loglikelihood is described by the equation
which contains these variables and terms:
— Coefficient of interest
— Profile loglikelihood function
— Nuisance coefficients
— Predictor input data
— Response input data
— Loglikelihood function for theta given and
Alternative Functionality
You can calculate both Wald and likelihood-ratio confidence intervals for several
coefficients using the coefCI function.
Version History
Introduced in R2025a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)