Perform Nonnegative Matrix Factorization
This example shows how to perform nonnegative matrix factorization.
Load the sample data.
load moore X = moore(:,1:5); rng('default'); % For reproducibility
Compute a rank-two approximation of X using a multiplicative update algorithm that begins from five random initial values for W and H.
opt = statset('MaxIter',10,'Display','final'); [W0,H0] = nnmf(X,2,'replicates',5,'options',opt,'algorithm','mult');
rep iteration rms resid |delta x|
1 10 358.296 0.00190554
2 10 78.3556 0.000351747
3 10 230.962 0.0172839
4 10 326.347 0.00739552
5 10 361.547 0.00705539
Final root mean square residual = 78.3556
The 'mult' algorithm is sensitive to initial values, which makes it a good choice when using 'replicates' to find W and H from multiple random starting values.
Now perform the factorization using alternating least-squares algorithm, which converges faster and more consistently. Run 100 times more iterations, beginning from the initial W0 and H0 identified above.
opt = statset('Maxiter',1000,'Display','final'); [W,H] = nnmf(X,2,'w0',W0,'h0',H0,'options',opt,'algorithm','als');
rep iteration rms resid |delta x|
1 2 77.5315 0.000830334
Final root mean square residual = 77.5315
The two columns of W are the transformed predictors. The two rows of H give the relative contributions of each of the five predictors in X to the predictors in W. Display H.
H
H = 2×5
0.0835 0.0190 0.1782 0.0072 0.9802
0.0559 0.0250 0.9969 0.0085 0.0497
The fifth predictor in X (weight 0.9802) strongly influences the first predictor in W. The third predictor in X (weight 0.9969) strongly influences the second predictor in W.
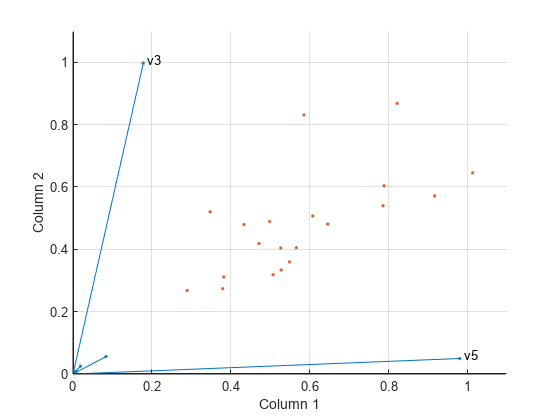
Visualize the relative contributions of the predictors in X with biplot, showing the data and original variables in the column space of W.
biplot(H','scores',W,'varlabels',{'','','v3','','v5'}); axis([0 1.1 0 1.1]) xlabel('Column 1') ylabel('Column 2')