procrustes
Procrustes analysis
Syntax
Description
d = procrustes(X,Y)X and Y, which are represented by configurations
of landmark points.
d = procrustes(X,Y,Name,Value)
Examples
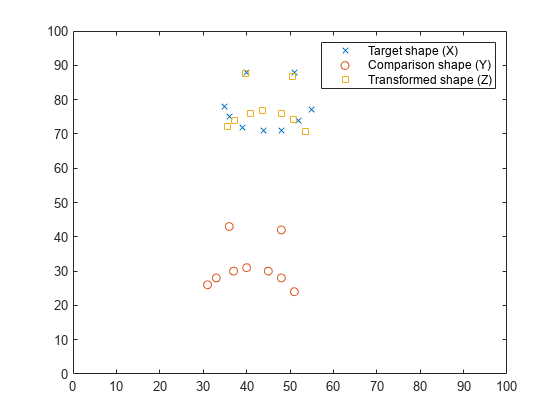
Construct matrices containing landmark points for two shapes, and visualize the shapes by plotting their landmark points.
X = [40 88; 51 88; 35 78; 36 75; 39 72; 44 71; 48 71; 52 74; 55 77]; Y = [36 43; 48 42; 31 26; 33 28; 37 30; 40 31; 45 30; 48 28; 51 24]; plot(X(:,1),X(:,2),"x") hold on plot(Y(:,1),Y(:,2),"o") xlim([0 100]) ylim([0 100]) legend("Target shape (X)","Comparison shape (Y)")

Compare the shapes and view their Procrustes distance.
[d,Z] = procrustes(X,Y)
d = 0.2026
Z = 9×2
39.7694 87.5089
50.5616 86.8011
35.5487 72.1631
37.3131 73.9909
40.8735 75.8503
43.5517 76.7959
48.0577 75.9771
50.7835 74.2286
53.5410 70.6841
Visualize the shape that results from superimposing Y onto X.
plot(Z(:,1),Z(:,2),"s") legend("Target shape (X)","Comparison shape (Y)", ... "Transformed shape (Z)") hold off
Use the Procrustes transformation returned by procrustes to analyze how it superimposes the comparison shape onto the target shape.
Generate sample data in two dimensions.
rng("default")
n = 10;
Y = normrnd(0,1,[n 2]);Create the target shape X by rotating Y 60 degrees (pi/3 in radians), scaling the size of Y by factor 0.5, and then translating the points by adding 2. Also, add some noise to the landmark points in X.
S = [cos(pi/3) -sin(pi/3); sin(pi/3) cos(pi/3)]
S = 2×2
0.5000 -0.8660
0.8660 0.5000
X = normrnd(0.5*Y*S+2,0.05,n,2);
Find the Procrustes transformation that can transform Y to X.
[~,Z,transform] = procrustes(X,Y);
Display the components of the Procrustes transformation.
transform
transform = struct with fields:
T: [2×2 double]
b: 0.4845
c: [10×2 double]
transform.T
ans = 2×2
0.4832 -0.8755
0.8755 0.4832
transform.c
ans = 10×2
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
2.0325 1.9836
transform.T is similar to the matrix S. Also, the scale component (transform.b) is close to 0.5, and the translation component values (transform.c) are close to 2.
Determine whether transform.T indicates a rotation or reflection by computing the determinant of transform.T. The determinant of a rotation matrix is 1, and the determinant of a reflection matrix is –1.
det(transform.T)
ans = 1
In two-dimensional space, a rotation matrix that rotates a point by an angle of degrees about the origin has the form
.
If you use either or , the rotation angle has two possible values between –180 and 180. Use both the and values to determine the rotation angle of the matrix without ambiguity. Using the atan2d function, you can determine the value from and , and also determine the angle.
theta = atan2d(transform.T(2,1),transform.T(1,1))
theta = 61.1037
transform.T is a rotation matrix of 61 degrees.
Use the Procrustes transformation returned by procrustes to analyze how it superimposes the comparison shape onto the target shape.
Create matrices with landmark points for two separate shapes.
X = [20 13; 20 20; 20, 29; 20 40; 12 36]; Y = [36 7; 36 10; 36 14; 36 20; 39 18];
Plot the landmark points to visualize the shapes.
plot(X(:,1),X(:,2),"-x") hold on plot(Y(:,1),Y(:,2),"-o") xlim([0 50]) ylim([0 50]) legend("Target shape (X)","Comparison shape (Y)") hold off

Obtain the Procrustes transformation by using procrustes.
[d,Z,transform] = procrustes(X,Y)
d = 0.0064
Z = 5×2
20.1177 13.3935
19.9145 19.6790
19.6435 28.0597
19.2371 40.6306
13.0871 36.2371
transform = struct with fields:
T: [2×2 double]
b: 2.0963
c: [5×2 double]
transform.T
ans = 2×2
-0.9995 -0.0323
-0.0323 0.9995
transform.c
ans = 5×2
96.0177 1.1661
96.0177 1.1661
96.0177 1.1661
96.0177 1.1661
96.0177 1.1661
The scale component of the transformation b indicates that the scale of X is about twice the scale of Y.
Find the determinant of the rotation and reflection component of the transformation.
det(transform.T)
ans = -1.0000
The determinant is –1, which means that the transformation contains a reflection.
In two-dimensional space, a reflection matrix has the form
,
which indicates a reflection over a line that makes an angle with the x-axis.
If you use either or , the angle for the line of reflection has two possible values between –90 and 90. Use both the and values to determine the angle for the line of reflection without ambiguity. Using the atan2d function, you can determine the value from and , and also determine the angle.
theta = atan2d(transform.T(2,1),transform.T(1,1))/2
theta = -89.0741
transform.T reflects points across a line that makes roughly a –90 degree angle with the x-axis; this line indicates the y-axis. The plots of X and Y show that reflecting across the y-axis is required to superimpose Y onto X.
Find the Procrustes transformation for landmark points, and apply the transformation to more points on the comparison shape than just the landmark points.
Create matrices with landmark points for two triangles X (target shape) and Y (comparison shape).
X = [5 0; 5 5; 8 5]; Y = [0 0; 1 0; 1 1];
Create a matrix with more points on the triangle Y.
Y_points = [linspace(Y(1,1),Y(2,1),10)' linspace(Y(1,2),Y(2,2),10)'
linspace(Y(2,1),Y(3,1),10)' linspace(Y(2,2),Y(3,2),10)'
linspace(Y(3,1),Y(1,1),10)' linspace(Y(3,2),Y(1,2),10)'];Plot both shapes, including the larger set of points for the comparison shape.
plot([X(:,1); X(1,1)],[X(:,2); X(1,2)],"bx-") hold on plot([Y(:,1); Y(1,1)],[Y(:,2); Y(1,2)],"ro-","MarkerFaceColor","r") plot(Y_points(:,1),Y_points(:,2),"ro") xlim([-1 10]) ylim([-1 6]) legend("Target shape (X)","Comparison shape (Y)", ... "Additional points on Y","Location","northwest")
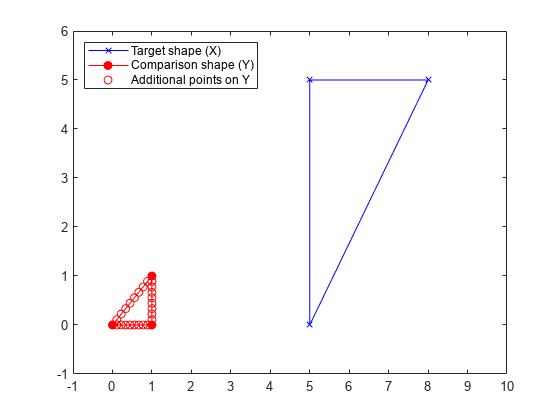
Call procrustes to obtain the Procrustes transformation from the comparison shape to the target shape.
[d,Z,transform] = procrustes(X,Y)
d = 0.0441
Z = 3×2
5.0000 0.5000
4.5000 4.5000
8.5000 5.0000
transform = struct with fields:
T: [2×2 double]
b: 4.0311
c: [3×2 double]
Use the Procrustes transformation to superimpose the other points (Y_points) on the comparison shape onto the target shape, and then visualize the results.
Z_points = transform.b*Y_points*transform.T + transform.c(1,:); plot([Z(:,1); Z(1,1)],[Z(:,2); Z(1,2)],"ks-","MarkerFaceColor","k") plot(Z_points(:,1),Z_points(:,2),"ks") legend("Target shape (X)","Comparison shape (Y)", ... "Additional points on Y","Transformed shape (Z)", ... "Transformed additional points","Location","best") hold off

Construct the shapes of the handwritten letters d and b using landmark points, and then plot the points to visualize the letters.
D = [33 93; 33 87; 33 80; 31 72; 32 65; 32 58; 30 72;
28 72; 25 69; 22 64; 23 59; 26 57; 30 57];
B = [48 83; 48 77; 48 70; 48 65; 49 59; 49 56; 50 66;
52 66; 56 65; 58 61; 57 57; 54 56; 51 55];
plot(D(:,1),D(:,2),"x-")
hold on
plot(B(:,1),B(:,2),"o-")
legend("Target shape (d)","Comparison shape (b)")
hold off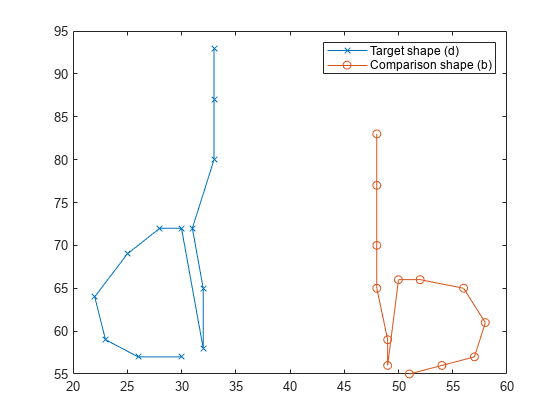
Use procrustes to compare the letters with reflection turned off, because reflection would turn the b into a d and not accurately preserve the shape you want to compare.
d = procrustes(D,B,"reflection",false)d = 0.3425
Try using procrustes with reflection on to see how the Procrustes distance differs.
d = procrustes(D,B,"reflection","best")
d = 0.0204
This reflection setting results in a smaller Procrustes distance because reflecting b better aligns it with d.
Construct two shapes represented by their landmark points, and then plot the points to visualize them.
X = [20 13; 20 20; 20 29; 20 40; 12 36]; Y = [36 7; 36 10; 36 14; 36 20; 39 18]; plot(X(:,1),X(:,2),"-x") hold on plot(Y(:,1),Y(:,2),"-o") xlim([0 50]) ylim([0 50]) legend("Target shape (X)","Comparison shape (Y)")

Compare the two shapes using Procrustes analysis with scaling turned off.
[d,Z] = procrustes(X,Y,"scaling",false)d = 0.2781
Z = 5×2
19.2194 20.8229
19.1225 23.8214
18.9932 27.8193
18.7993 33.8162
15.8655 31.7202
Visualize the superimposed landmark points.
plot(Z(:,1),Z(:,2),"-s") legend("Target shape (X)","Comparison shape (Y)", ... "Transformed shape (Z)") hold off

The superimposed shape Z does not differ in scale from the original shape Y.
Input Arguments
Target shape, specified as an n-by-p matrix where each of the n rows contains a p-dimensional landmark point. The landmark points represent the shape that is the target of the comparison.
Data Types: single | double
Comparison shape, specified as an n-by-q matrix where each of the n rows contains a q-dimensional landmark point with q ≤ p. The landmark points represent the shape to be compared with the target shape.
Y must have the same number of points (rows) as
X, where each point in Y,
Y(i,:) corresponds to the point in the same row in
X, X(i,:).
Points in Y can have fewer dimensions (number of columns) than
points in X. In this case, procrustes appends
columns of zeros to Y to match the dimensions of
X.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: d = procrustes(X,Y,"Scaling",false,"reflection",false)
performs Procrustes analysis without scaling or reflection in the
transformation.
Flag to enable scaling in the Procrustes transformation, specified as logical
1 (true) or 0
(false). A value of false prevents scaling in
the transformation. A value of true allows scaling if it minimizes
the differences between the landmark points in X and
Y.
Set Scaling to false to compare
Y to X without scaling
Y to match the scale of X. This option
causes shapes of different scales to have a greater Procrustes distance.
Example: "Scaling",false
Data Types: logical
Flag to enable reflection in the Procrustes transformation, specified as
"best", logical 1 (true),
or logical 0 (false).
"best"— Find the optimal Procrustes transformation, regardless of whether or not it contains a reflection.1(true) — Force the Procrustes transformation to reflectY, whether or not the transformation minimizes the differences between the landmark points.0(false) — Prevent the Procrustes transformation from reflectingY. This option does not prevent rotation in the transformation.
Set Reflection to false to
compare Y to X without reflecting
Y to match the shape of X. This option
causes shapes that are reflections of each other to have a greater Procrustes
distance.
Example: "Reflection",true
Data Types: logical | string | char
Output Arguments
Squared Procrustes distance, a measure of dissimilarity between two shapes, returned
as a numeric scalar in the range [0,1]. If
Scaling is set to false, the squared
Procrustes distance can be outside of the range [0,1].
procrustes computes the distance using the sum of squared
differences between the corresponding points in X and
Z. The function then standardizes the distance by the scale of
X. The scale of X is
sum(sum((X-mean(X)).^2)), which is the sum of squared elements of a
centered version of X where the columns of X
have mean 0.
Data Types: single | double
Procrustes transformation, returned as a structure with three fields:
T— Rotation and reflection component, specified by a p-by-p transformation matrix that rotates or reflectsYto match the orientation of the landmark points inX.If
Tis a rotation matrix, thendet(T)is 1.If
Tis a reflection matrix, thendet(T)is –1.
b— Scale component, specified by a scalar to stretch (b> 1), conserve (b= 1), or shrink (b< 1) the scale ofYto match the scale ofX.c— Translation component, specified by an n-by-p matrix where each row is the p-dimensional vector to add to the points inYto shift it ontoX.
The Procrustes transformation superimposes Y onto
X by performing the following transformation:
Z = bYT + c.
Set the Reflection name-value argument to
false to ensure that transform.T does not
contain a reflection.
Set the Scaling name-value argument to false
to remove the scale component, fixing transform.b to
1.
Data Types: struct
More About
The Procrustes distance is a measure of dissimilarity between shapes based on Procrustes analysis.
The procrustes function finds the Procrustes transformation, which
is the best shape-preserving Euclidean transformation (consisting of rotation, reflection,
scaling, and translation) between the two shapes X and
Y. The Procrustes transformation is an optimal transformation that
minimizes the sum of squared differences between the landmark points in
X and Z, where Z is the
transformed shape of Y that results from superimposing
Y onto X.
The procrustes function returns the squared Procrustes distance
(d), transformed shape (Z), and Procrustes
transformation (transform). The squared Procrustes distance is the sum
of squared differences between X and Z.
Tips
Procrustes analysis is appropriate when all dimensions in
XandYhave similar scales. If the columns ofXandYhave different scales, standardize the columns by usingzscoreornormalize.Procrustes analysis is useful in conjunction with multidimensional scaling. Two different applications of multidimensional scaling can produce reconstructed points that are similar in principle, but look different because they have different orientations. Also, the reconstructed points can have a different orientation than the original points. The
procrustesfunction transforms one set of points to make them more comparable to the other. For an example, see Classical Multidimensional Scaling Applied to Nonspatial Distances.
References
[1] Kendall, David G. “A Survey of the Statistical Theory of Shape.” Statistical Science. Vol. 4, No. 2, 1989, pp. 87–99.
[2] Bookstein, Fred L. Morphometric Tools for Landmark Data. Cambridge, UK: Cambridge University Press, 1991.
[3] Seber, G. A. F. Multivariate Observations. Hoboken, NJ: John Wiley & Sons, Inc., 1984.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)