Visualize Multivariate Data
This example shows how to visualize multivariate data using statistical plots. Many statistical analyses involve only two variables: a predictor variable and a response variable. Two variables are easy to visualize using plots such as 2D scatter plots, bivariate histograms, and box plots. You can also visualize trivariate data with 3D scatter plots, or 2D scatter plots with a third variable represented by color. However, many data sets involve a larger number of variables, making direct visualization more difficult. This example explores how to visualize high-dimensional data using functions in Statistics and Machine Learning Toolbox™.
Load Data
Load the carbig data set, which contains measurements for about 400 cars made in the 1970s and 1980s. Use multivariate visualizations to explore the values for fuel efficiency (in miles per gallon, MPG), acceleration (time from 0–60 mph in seconds), engine displacement (in cubic inches), weight, and horsepower.
load carbig X = [MPG,Acceleration,Displacement,Weight,Horsepower]; varNames = ["MPG","Acceleration","Displacement","Weight","Horsepower"];
Scatter Plot Matrices
One way to view high-dimensional data is to display slices of the data in lower dimensional subspaces. Use the gplotmatrix function to display an array of all the bivariate scatter plots for the five variables in X, along with a univariate histogram for each variable. Group observations by the number of cylinders.
gplotmatrix(X,[],Cylinders,[],[],8,[],[],varNames)

The points in each scatter plot are color coded by the number of cylinders: red for 4 cylinders, purple for 6, and green for 8. Cars with rotary engines have 3 cylinders, and a few cars have 5 cylinders. This array of plots helps you to find patterns in the relationships between pairs of variables. Important patterns in higher dimensions might exist, but they are not easy to recognize in this plot.
Parallel Coordinates Plots
While the scatter plot matrix displays only bivariate relationships, some plots display all the variables together and allow you to investigate higher dimensional relationships among variables. The most straightforward multivariate plot is the parallel coordinates plot. The coordinate axes in this plot are laid out horizontally instead of orthogonally as in a typical Cartesian graph. Each observation is represented in the plot as a series of connected line segments.
Create a plot of all the cars in X with 4, 6, or 8 cylinders, and use color to group the observations.
cyl468 = ismember(Cylinders,[4 6 8]); parallelcoords(X(cyl468,:),Group=Cylinders(cyl468), ... Standardize="on",Labels=varNames)
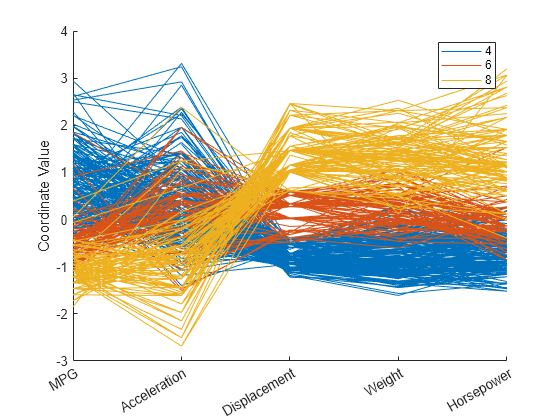
The horizontal direction in this plot represents the coordinate axes, and the vertical direction represents the data. Each observation consists of measurements on five variables, and each measurement is represented as the height at which the corresponding line crosses each coordinate axis. Because the five variables have widely different ranges, each variable in the plot is standardized to have a mean of 0 and a variance of 1. The color coding in the graph shows that eight-cylinder cars tend to have low values for MPG and acceleration, and high values for displacement, weight, and horsepower.
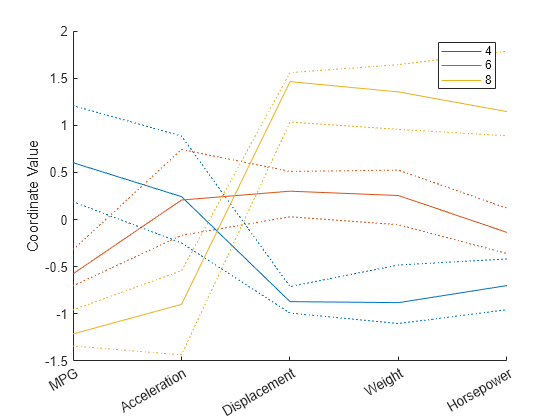
A parallel coordinates plot with a large number of observations might be difficult to read. To alleviate this problem, you can create a parallel coordinates plot that displays only the median and the upper and lower quartiles (25% and 75% points) for each group. This plot allows you to better distinguish between groups, but does not include observations that might be of interest, such as group outliers.
parallelcoords(X(cyl468,:),Group=Cylinders(cyl468), ... Standardize="on",Labels=varNames,Quantile=0.25)
Andrews Plots
Another type of multivariate visualization is the Andrews plot. This plot represents each observation as a smooth function over the interval [0,1].
andrewsplot(X(cyl468,:),Group=Cylinders(cyl468),Standardize="on")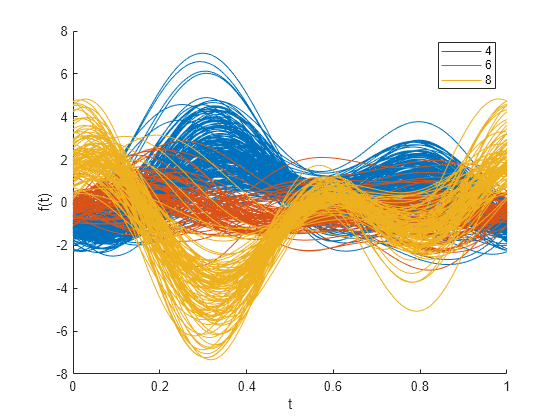
Each function is a Fourier series, with coefficients equal to the corresponding observation's values. In this example, the series has five terms: a constant, two sine terms with periods 1 and 1/2, and two similar cosine terms. The three leading terms have the most apparent effect on the shape of each function. That is, you can most easily recognize patterns in the first three variables.
The plot shows a distinct difference between the groups at t = 0. This difference indicates that the first variable, MPG, is one of the features that distinguishes cars with 4, 6, or 8 cylinders from each other. The difference between the groups at around t = 1/3 is also interesting. Enter this value in the formula for the Andrews plot function. The result is a set of coefficients that defines a linear combination of the variables. This linear combination helps you distinguish one group from another.
t1 = 1/3; coeffs = [1/sqrt(2) sin(2*pi*t1) cos(2*pi*t1) sin(4*pi*t1) cos(4*pi*t1)]
coeffs = 1×5
0.7071 0.8660 -0.5000 -0.8660 -0.5000
The coefficients indicate that four-cylinder cars, compared to eight-cylinder cars, have higher values of MPG and acceleration, and lower values of displacement, horsepower, and particularly weight. This conclusion matches the one from the parallel coordinates plot.
Glyph Plots
You can also visualize multivariate data by using glyphs to represent the dimensions. The function glyphplot supports two types of glyphs: stars and Chernoff faces. Create a star plot of the first nine car models in the data set. Each spoke in a star represents one variable, and the spoke length is proportional to the value of the variable for that observation.
g = glyphplot(X(1:9,:),Glyph="star",VarLabels=varNames, ... ObsLabels=Model(1:9,:)); set(g(:,3),FontSize=8);
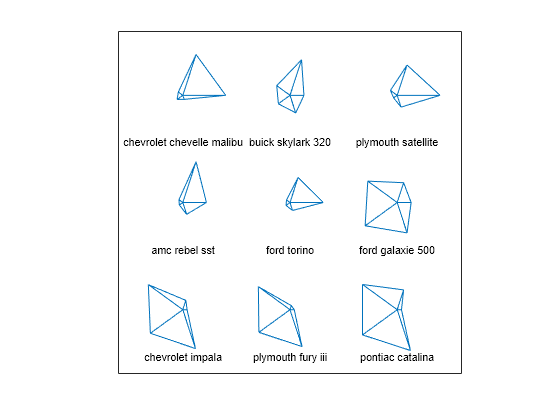
In a figure window, this plot allows you to explore the data values interactively by using data cursors. For example, clicking the rightmost point of the star for the Ford Torino shows that the car has an MPG value of 17.
Glyph Plots and Multidimensional Scaling
If you plot stars on a grid in no particular order, you can sometimes create a figure in which adjacent stars look quite different. You might not be able to recognize any pattern visually. To help with pattern recognition, combine multidimensional scaling (MDS) with a glyph plot.
First, select all cars from 1977, and then use the zscore function to standardize each of the five variables to have a mean of 0 and a variance of 1. Then, compute the Euclidean distances among the standardized observations as a measure of dissimilarity. For a more complex application, consider using a less simplistic measure of dissimilarity.
models77 = find((Model_Year==77)); dissimilarity = pdist(zscore(X(models77,:)));
Finally, use mdscale to create a set of locations in two dimensions, whose interpoint distances approximate the dissimilarities among the original high-dimensional data points. Plot the glyphs using these locations. The distances in the resulting 2D plot roughly reproduce the data.
Y = mdscale(dissimilarity,2); figure glyphplot(X(models77,:),Glyph="star",Centers=Y, ... VarLabels=varNames,ObsLabels=Model(models77,:),Radius=0.5) title("1977 Model Year")
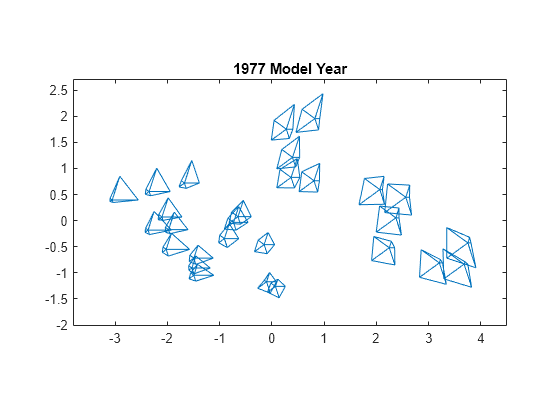
The 2D plot uses MDS as the dimension reduction method. Typically, a reduction in dimensionality implies a loss of information, but the glyphs include all the high-dimensional information in the data. The purpose of using MDS is to impose some regularity on the variation in the data, so that you can see patterns among the glyphs more easily.
As with the previous plot, you can use a figure window to explore this plot interactively.
Another type of glyph is the Chernoff face. This glyph encodes the data values for each observation into facial features, such as the size of the face, shape of the face, position of the eyes, and so on. The correspondence of features to variables determines what relationships are easiest to see in the plot. Use glyphplot to specify this correspondence.
figure facePlot = glyphplot(X(models77,:),Glyph="face",Centers=Y, ... VarLabels=varNames,ObsLabels=Model(models77,:)); set(facePlot(:,1:2),Color="#D95319") title("1977 Model Year")

In this plot, the two most apparent features—face size and relative forehead-to-jaw size—encode the MPG and acceleration variables, respectively. The forehead and jaw shapes encode the displacement and weight variables, respectively. The width between the eyes encodes the horsepower variable. Note that few faces have wide foreheads and narrow jaws, and vice versa, which indicates a positive linear correlation between displacement and weight. This result matches the results from the scatter plot matrix.
See Also
gplotmatrix | parallelcoords | andrewsplot | glyphplot