cell2sym
Convert cell array to symbolic array
Description
S = cell2sym(C)C to a symbolic array S.
The elements of C must be convertible to symbolic
objects.
If each element of the input cell array C is
a scalar, then size(S) = size(C), and S(k)
= sym(C(k)) for all indices k. If the
cell array C contains nonscalar elements, then
the contents of C must support concatenation
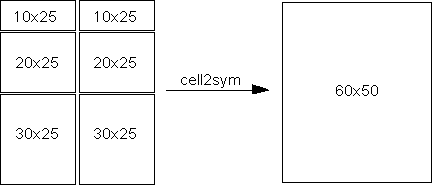
into an N-dimensional rectangle. Otherwise, the results are undefined.
For example, the contents of cells in the same column must have the
same number of columns. However, they do not need to have the same
number of rows. See figure.
Examples
Input Arguments
Output Arguments
Version History
Introduced in R2016a