Fiala Wheel 2DOF

Fiala wheel 2DOF wheel with disc, drum, or mapped brake

• Library:

• Vehicle Dynamics Blockset / Wheels and Tires

• 

×

Description

The Fiala Wheel 2DOF block implements a simplified tire with lateral and longitudinal slip capability based on the E. Fiala model^[1]. The block uses a translational friction model to calculate the forces and moments during combined longitudinal and lateral slip, requiring fewer parameters than the Combined Slip Wheel 2DOF block. If you do not have the tire coefficients needed by the Magic Formula, consider using this block for studies that do not involve extensive nonlinear combined lateral slip or lateral dynamics. If your study does require nonlinear combined slip or lateral dynamics, consider using the Combined Slip Wheel 2DOF block.

The block determines the wheel rotation rate, vertical motion, and forces and moments in all six degrees-of-freedom (DOFs) based on the driveline torque, brake pressure, road height, wheel camber angle, and inflation pressure. You can use this block for these types of analyses:

• Driveline and vehicle simulations that require low frequency tire-road and braking forces for vehicle acceleration, braking, and wheel rolling resistance calculations with minimal tire parameters.

• Wheel interaction with an idealized road surface.

• Ride and handling maneuvers for vehicles undergoing mild combined slip. For this analysis, you can connect the block to driveline and chassis components such as differentials, suspension, and vehicle body systems.

• Yaw stability. For this analyses, you can connect this block to more detailed braking system models.

• Tire stiffness and unsprung mass interactions with ground variations, load transfer, or chassis motion using the block vertical DOF.

The block integrates rotational wheel, vertical mass, and braking dynamics models. For the slip-dependent tire forces and moments, the block implements the Fiala tire model.

Use the Brake Type parameter to select the brake.

Goal	Brake Type Setting
No braking	None
Implement brake that converts the brake cylinder pressure into a braking force	Disc
Implement simplex drum brake that converts the applied force and brake geometry into a net braking torque	Drum
Implement lookup table that is a function of the wheel speed and applied brake pressure	Mapped

To calculate the rolling resistance torque, specify one of these Rolling Resistance parameters.

Setting	Block Implementation
None	None
Pressure and velocity	Method in Stepwise Coastdown Methodology for Measuring Tire Rolling Resistance. The rolling resistance is a function of tire pressure, normal force, and velocity.
ISO 28580	Method specified in ISO 28580:2018, Passenger car, truck and bus tyre rolling resistance measurement method — Single point test and correlation of measurement results.
Magic Formula	Magic formula equations from 4.E70 in Tire and Vehicle Dynamics. The magic formula is an empirical equation based on fitting coefficients.
Mapped torque	Lookup table that is a function of the normal force and spin axis longitudinal velocity.

To calculate vertical motion, specify one of these Vertical Motion parameters.

Setting	Block Implementation
None	Block passes the applied chassis forces directly through to the rolling resistance and longitudinal force calculations.
Mapped stiffness and damping	Vertical motion depends on wheel stiffness and damping. Stiffness is a function of tire sidewall displacement and pressure. Damping is a function of tire sidewall velocity and pressure.

Rotational Wheel Dynamics

The block calculates the inertial response of the wheel subject to:

• Axle losses

• Brake and drive torque

• Tire rolling resistance

• Ground contact through the tire-road interface

The input torque is the summation of the applied axle torque, braking torque, and moment arising from the combined tire torque.

$$T_i=T_a-T_b+T_d$$

For the moment arising from the combined tire torque, the block implements tractive wheel forces and rolling resistance with first-order dynamics. The rolling resistance has a time constant parameterized in terms of a relaxation length.

$$T_d(s)=\frac{1}{\frac{\left|\omega \right|R_e}{L_e}s+1}(F_x{R}_e+M_y)$$

To calculate the rolling resistance torque, you can specify one of these Rolling Resistance parameters.

Setting	Block Implementation
None	Block sets rolling resistance, My, to zero.
Pressure and velocity	Block uses the method in SAE Stepwise Coastdown Methodology for Measuring Tire Rolling Resistance. The rolling resistance is a function of tire pressure, normal force, and velocity. Specifically, $$M_y=R_e\{a+b\left|V_x\right|+c{V}_x{}^2\}\left\{F_z{}^{\beta }{p}_i{}^{\alpha }\right\}\tanh \left(4V_x\right)$$
ISO 28580	Block uses the method specified in ISO 28580:2018, Passenger car, truck and bus tyre rolling resistance measurement method — Single point test and correlation of measurement results. The method accounts for normal load, parasitic loss, and thermal corrections from test conditions. Specifically, $$M_y=R_e(\frac{F_z{C}_r}{1+K_t(T_{amb}-T_{meas})}-F_{pl})\tanh (\omega )$$
Magic Formula	Block calculates the rolling resistance, My, using the Magic Formula equations from 4.E70 in Tire and Vehicle Dynamics. The magic formula is an empirical equation based on fitting coefficients.
Mapped torque	For the rolling resistance, My, the block uses a lookup table that is a function of the normal force and spin axis longitudinal velocity.

If the brakes are enabled, the block determines the braking locked or unlocked condition based on an idealized dry clutch friction model. Based on the lock-up condition, the block implements these friction and dynamic models.

If	Lock-Up Condition	Friction Model	Dynamic Model
$\begin{array}{l}\omega \ne 0\\ \text{or}\\ T_S<\left|T_i+T_f-\omega b\right|\end{array}$	Unlocked	$$\begin{array}{l}{T}_f=T_k\\ \text{where,}\\ T_k=F_c{R}_{eff}{\mu }_k\tanh \left[4\left(-{\omega }_d\right)\right]\\ T_s=F_c{R}_{eff}{\mu }_s\\ R_{eff}=\frac{2(R_o{}^3-R_i{}^3)}{3(R_o{}^2-R_i{}^2)}\end{array}$$	$$\dot{\omega }J=-\omega b+T_i+T_o$$
$\begin{array}{l}\omega =0\\ \text{and}\\ T_S\ge \left|T_i+T_f-\omega b\right|\end{array}$	Locked	$$T_f=T_s$$	$$\omega =0$$

The equations use these variables.

ω	Wheel angular velocity
a	Velocity-independent force component
b	Linear velocity force component
c	Quadratic velocity force component
Le	Tire relaxation length
J	Moment of inertia
My	Rolling resistance torque
Ta	Applied axle torque
Tb	Braking torque
Td	Combined tire torque
Tf	Frictional torque
Ti	Net input torque
Tk	Kinetic frictional torque
To	Net output torque
Ts	Static frictional torque
Fc	Applied clutch force
Fx	Longitudinal force developed by the tire road interface due to slip
Reff	Effective clutch radius
Ro	Annular disk outer radius
Ri	Annular disk inner radius
Re	Effective tire radius while under load and for a given pressure
Vx	Longitudinal axle velocity
Fz	Vehicle normal force
Cr	Rolling resistance constant
Tamb	Ambient temperature
Tmeas	Measured temperature for rolling resistance constant
Fpl	Parasitic force loss
Kt	Thermal correction factor
ɑ	Tire pressure exponent
β	Normal force exponent
pi	Tire pressure
μs	Coefficient of static friction
μk	Coefficient of kinetic friction

Longitudinal Force

The block implements the longitudinal force as a function of wheel slip relative to the road surface using these equations.

Calculation	Equation
Critical slip	$$\kappa {\text{'}}_{Critical}=\left|\frac{\mu F_z}{2C_{\kappa }}\right|$$
Longitudinal force	$$F_x=\{\begin{array}{c}{C}_k \kappa \text{'}\text{ when }\left|{\kappa }^{\text{'}}\right|\le {\kappa }^{\text{'}}{}_{Critical}\\ \text{tanh}(4\kappa \text{'})\left(\mu \left|F_z\right|-\left|\frac{{\left(\mu F_z\right)}^2}{4\kappa \text{'}{C}_{\kappa }}\right|\right) \text{ when }\left|{\kappa }^{\text{'}}\right|>{\kappa }^{\text{'}}{}_{Critical}\end{array}$$
Friction coefficient	$\mu =({\mu }_s-({\mu }_s-{\mu }_k){\kappa }_{k\alpha }){\lambda }_{\mu }$
Slip coefficient	${\kappa }_{k\alpha }=\sqrt{\kappa {\text{'}}^2+{\text{tan}}^2(\alpha \text{'})}$

The equations use these variables.

κ'	Slip state
Fx	Longitudinal force acting on axle along tire-fixed x-axis,
Cκ	Longitudinal stiffness
Fz	Vertical contact patch normal force along tire-fixed z-axis,
μ	Friction coefficient
μs	Coefficient of static friction
μk	Coefficient of kinetic friction
κka	Comprehensive slip coefficient
α'	Slip angle state
λμ	Friction scaling

Lateral Force

The block implements the lateral force as a function of wheel slip angle state using these equations.

Calculation	Equation
Critical slip angle	$\alpha {\text{'}}_{Critical}=\text{atan}(\frac{3\mu \left|F_z\right|}{C_a})$
Lateral force	$$\begin{array}{l}{F}_y=\{\begin{array}{c}-\text{tanh}(4\alpha \text{'})\mu \left|F_z\right| \text{ when }\left|\alpha \text{'}\right|>\alpha {\text{'}}_{Critical}\\ -\tanh \left(4\alpha \text{'}\right)\mu \left|F_z\right|\left(1-{\xi }^3\right)+\gamma C_{\gamma }\text{ when }\left|\alpha \text{'}\right|\le \alpha {\text{'}}_{Critical}\end{array}\\ \\ \xi =1-\frac{C_a\left|\text{tan}(\alpha \text{'})\right|}{3\mu \left|F_z\right|}\end{array}$$

The equations use these variables.

α'	Slip angle state
Fy	Lateral force acting on axle along tire-fixed y-axis,
Fz	Vertical contact patch normal force along tire-fixed z-axis
Cɣ	Camber stiffness
Cα	Lateral stiffness per slip angle
μ	Friction coefficient

Vertical Dynamics

For the vertical dynamics, the block implements these equations.

Calculation	Equation
Vertical response	$\ddot{z}m=F_{ztire}+mg-Fz$
Tire normal force	$F_{ztire}={\rho }_{z}k-b\dot{z}$
Vertical sidewall deflection	${\rho }_z=z_{gnd}-z,z\ge 0$

The equations use these variables.

z	Tire deflection along tire-fixed z-axis
zgnd	Ground displacement along tire-fixed z-axis
Fztire	Tire normal force along tire-fixed z-axis
Fz	Vertical force acting on axle along tire-fixed z-axis
ρz	Vertical sidewall deflection along tire-fixed z-axis
k	Vertical sidewall stiffness
b	Vertical sidewall damping

Overturning, Aligning, and Scaling

This table summarizes the overturning, aligning, and scaling implementation.

Calculation	Implementation
Overturning moment	The Fiala model does not define an overturning moment. The block implements this equation, requiring minimal parameters. $M_x=F_y{R}_e\text{cos}(\gamma )$
Aligning moment	The block implements the aligning moment as a combination of yaw rate damping and slip angle state. $$\begin{array}{l}{M}_z=\{\begin{array}{c}\dot{\psi }{b}_{M_z}\text{ when }\left|\alpha \text{'}\right|>\alpha {\text{'}}_{Critical}\\ \tanh \left(4{\alpha }^{\text{'}}\right)w\mu \left|{\text{F}}_z\right|\left(1-\xi \right){\xi }^3+\dot{\psi }{b}_{M_z}\text{ when }\left|\alpha \text{'}\right|\le \alpha {\text{'}}_{Critical}\end{array}\\ \\ \xi =1-\frac{C_a\left|\text{tan}(\alpha \text{'})\right|}{3\mu \left|F_z\right|}\end{array}$$
Friction scaling	To vary the coefficient of friction, use the ScaleFctr input port.

The equations use these variables.

Mx	Overturning moment acting on axle about tire-fixed x-axis
Mz	Aligning moment acting on axle about tire-fixed z-axis
Re	Effective contact patch to wheel carrier radial distance
ɣ	Camber angle
k	Vertical sidewall stiffness
b	Vertical sidewall damping
$\dot{\psi }$	Tire angular velocity about the tire-fixed z-axis (yaw rate)
w	Tire width
α'	Slip angle state
bMz	Linear yaw rate resistance
Fy	Lateral force acting on axle along tire-fixed y-axis
Cɣ	Camber stiffness
Cα	Lateral stiffness per slip angle
μ	Friction coefficient
Fz	Vertical contact patch normal force along tire-fixed z-axis

Tire and Wheel Coordinate Systems

To resolve the forces and moments, the block uses the Z-Up orientation of the tire and wheel coordinate systems.

• Tire coordinate system axes (X_T, Y_T, Z_T) are fixed in a reference frame attached to the tire. The origin is at the tire contact with the ground.

• Wheel coordinate system axes (X_W, Y_W, Z_W) are fixed in a reference frame attached to the wheel. The origin is at the wheel center.

Z-Up Orientation^[1]

Brakes

Disc

If you specify the Brake Type parameter Disc, the block implements a disc brake. This figure shows the side and front views of a disc brake.

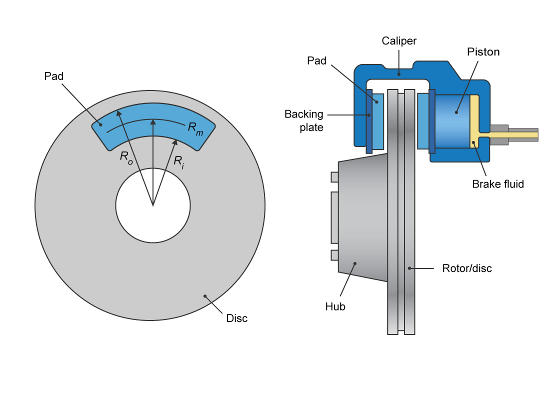
A disc brake converts brake cylinder pressure from the brake cylinder into force. The disc brake applies the force at the brake pad mean radius.

The block uses these equations to calculate brake torque for the disc brake.

$T=\{\begin{array}{c}\frac{\mu P\pi B_a{}^2{R}_m{N}_{pads}}{4} \text{ when }N\ne 0\\ \frac{{\mu }_{static}P\pi B_a{}^2{R}_m{N}_{pads}}{4} \text{ when }N=0\end{array}$

$$Rm=\frac{Ro+Ri}{2}$$

The equations use these variables.

T	Brake torque
P	Applied brake pressure
N	Wheel speed
Npads	Number of brake pads in disc brake assembly
μstatic	Disc pad-rotor coefficient of static friction
μ	Disc pad-rotor coefficient of kinetic friction
Ba	Brake actuator bore diameter
Rm	Mean radius of brake pad force application on brake rotor
Ro	Outer radius of brake pad
Ri	Inner radius of brake pad

Drum

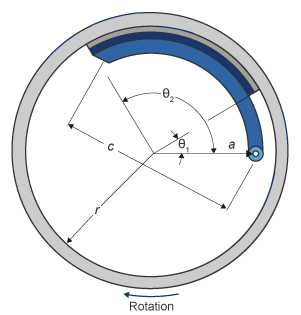
If you specify the Brake Type parameter Drum, the block implements a static (steady-state) simplex drum brake. A simplex drum brake consists of a single two-sided hydraulic actuator and two brake shoes. The brake shoes do not share a common hinge pin.

The simplex drum brake model uses the applied force and brake geometry to calculate a net torque for each brake shoe. The drum model assumes that the actuators and shoe geometry are symmetrical for both sides, allowing a single set of geometry and friction parameters to be used for both shoes.

The block implements equations that are derived from these equations in Fundamentals of Machine Elements.

$\begin{array}{l}{T}_{rshoe}=\left(\frac{\pi \mu cr(\cos {\theta }_2-\cos {\theta }_1)B_a{}^2}{2\mu (2r\left(\cos {\theta }_2-\cos {\theta }_1)+a\left({\cos }^2{\theta }_2-{\cos }^2{\theta }_1\right)\right)+ar\left(2{\theta }_1-2{\theta }_2+\sin 2{\theta }_2-\sin 2{\theta }_1\right)}\right)P\\ \\ T_{lshoe}=\left(\frac{\pi \mu cr(\cos {\theta }_2-\cos {\theta }_1)B_a{}^2}{-2\mu (2r\left(\cos {\theta }_2-\cos {\theta }_1)+a\left({\cos }^2{\theta }_2-{\cos }^2{\theta }_1\right)\right)+ar\left(2{\theta }_1-2{\theta }_2+\sin 2{\theta }_2-\sin 2{\theta }_1\right)}\right)P\end{array}$

$T=\{\begin{array}{c}{T}_{rshoe}+T_{lshoe}\text{ when }N\ne 0\\ (T_{rshoe}+T_{lshoe})\frac{{\mu }_{static}}{\mu }\text{ when }N=0\end{array}$

The equations use these variables.

T	Brake torque
P	Applied brake pressure
N	Wheel speed
μstatic	Disc pad-rotor coefficient of static friction
μ	Disc pad-rotor coefficient of kinetic friction
Trshoe	Right shoe brake torque
Tlshoe	Left shoe brake torque
a	Distance from drum center to shoe hinge pin center
c	Distance from shoe hinge pin center to brake actuator connection on brake shoe
r	Drum internal radius
Ba	Brake actuator bore diameter
Θ1	Angle from shoe hinge pin center to start of brake pad material on shoe
Θ2	Angle from shoe hinge pin center to end of brake pad material on shoe

Mapped

If you specify the Brake Type parameter Mapped, the block uses a lookup table to determine the brake torque.

$T=\{\begin{array}{c}{f}_{brake}(P,N) \text{ when }N\ne 0\\ \left(\frac{{\mu }_{static}}{\mu }\right)f_{brake}(P,N) \text{ when }N=0\end{array}$

The equations use these variables.

T	Brake torque
$f_{brake}^{}(P,N)$	Brake torque lookup table
P	Applied brake pressure
N	Wheel speed
μstatic	Friction coefficient of drum pad-face interface under static conditions
μ	Friction coefficient of disc pad-rotor interface

The lookup table for the brake torque, $f_{brake}^{}(P,N)$, is a function of applied brake pressure and wheel speed, where:

• T is brake torque, in N·m.

• P is applied brake pressure, in bar.

• N is wheel speed, in rpm.

Ports

Input

BrkPrs — Brake pressure

scalar | N-by-1 vector

Brake pressure, in Pa.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Dependencies

To enable this port, for the Brake Type parameter, specify one of these types:

• Disc

• Drum

• Mapped

AxlTrq — Axle torque

scalar | N-by-1 vector

Axle torque, T_a, about wheel spin axis, in N·m.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Vx — Longitudinal velocity

scalar | N-by-1 vector

Axle longitudinal velocity, V_x, along tire-fixed x-axis, in m/s.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Vy — Lateral velocity

scalar | N-by-1 vector

Axle lateral velocity, V_y, along tire-fixed y-axis, in m/s.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Camber — Inclination angle

scalar | N-by-1 vector

Camber angle, ɣ, or inclination angle, ε, in rad.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

YawRate — Tire angular velocity

scalar | N-by-1 vector

Tire angular velocity, r, about the tire-fixed z-axis (yaw rate), in rad/s.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Prs — Tire inflation pressure

scalar | N-by-1 vector

Tire inflation pressure, p_i, in Pa.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Gnd — Ground displacement

scalar | N-by-1 vector

Ground displacement along tire-fixed z-axis, in m. Positive input produces wheel lift.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Fext — Axle force applied to tire

scalar | N-by-1 vector

Axle force applied to tire, F_ext, along vehicle-fixed z-axis (positive input compresses the tire), in N.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

ScaleFctrs — Scale factor

scalar | N-by-1 vector

Scale factor to account for variations in the coefficient of friction.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Output

Info — Block data

bus

Block data, returned as a bus signal containing these block values.

Signal	Description	Units
AxlTrq	Axle torque about wheel-fixed y-axis	N·m
Omega	Wheel angular velocity about wheel-fixed y-axis	rad/s
Fx	Longitudinal vehicle force along tire-fixed x-axis	N
Fy	Lateral vehicle force along tire-fixed y-axis	N
Fz	Vertical vehicle force along tire-fixed z-axis	N
Mx	Overturning moment about tire-fixed x-axis	N·m
My	Rolling resistance torque about tire-fixed y-axis	N·m
Mz	Aligning moment about tire-fixed z-axis	N·m
Vx	Vehicle longitudinal velocity along tire-fixed x-axis	m/s
Vy	Vehicle lateral velocity along tire-fixed y-axis	m/s
Re	Loaded effective radius	m
Kappa	Longitudinal slip ratio	NA
Alpha	Side slip angle	rad
a	Contact patch half length	m
b	Contact patch half width	m
Gamma	Camber angle	rad
psidot	Tire angular velocity about the tire-fixed z-axis (yaw rate)	rad/s
BrkTrq	Brake torque about the vehicle-fixed y-axis	N·m
BrkPrs	Brake pressure	Pa
z	Axle vertical displacement along tire-fixed z-axis	m
zdot	Axle vertical velocity along tire-fixed z-axis	m/s
Gnd	Ground displacement along tire-fixed z-axis (positive input produces wheel lift)	m
GndFz	Vertical sidewall force on ground along tire-fixed z-axis	N
Prs	Tire inflation pressure	Pa

Omega — Wheel angular velocity

scalar | N-by-1 vector

Wheel angular velocity, ω, about wheel-fixed y-axis, in rad/s.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Fx — Longitudinal axle force

scalar | N-by-1 vector

Longitudinal force acting on axle, F_x, along tire-fixed x-axis, in N. Positive force acts to move the vehicle forward.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Fy — Lateral axle force

scalar | N-by-1 vector

Lateral force acting on axle, F_y, along tire-fixed y-axis, in N.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Fz — Vertical axle force

scalar | N-by-1 vector

Vertical force acting on axle, F_z, along tire-fixed z-axis, in N.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Mx — Overturning moment

scalar | N-by-1 vector

Longitudinal moment acting on axle, M_x, about tire-fixed x-axis, in N·m.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

My — Rolling resistive moment

scalar | N-by-1 vector

Lateral moment acting on axle, M_y, about tire-fixed y-axis, in N·m.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Mz — Aligning moment

scalar | N-by-1 vector

Vertical moment acting on axle, M_z, about tire-fixed z-axis, in N·m.

Vector is the number of wheels, N, by 1. If you provide a scalar value, the block assumes that number of wheels is one.

Parameters

Block Options

Brake Type — Select type

None | Disc | Drum | Mapped

Use the Brake Type parameter to select the brake.

Goal	Brake Type Setting
No braking	None
Implement brake that converts the brake cylinder pressure into a braking force	Disc
Implement simplex drum brake that converts the applied force and brake geometry into a net braking torque	Drum
Implement lookup table that is a function of the wheel speed and applied brake pressure	Mapped

Rolling Resistance — Select type

None (default) | Pressure and velocity | ISO 28580 | Magic Formula | Mapped torque

To calculate the rolling resistance torque, specify one of these Rolling Resistance parameters.

Setting	Block Implementation
None	None
Pressure and velocity	Method in Stepwise Coastdown Methodology for Measuring Tire Rolling Resistance. The rolling resistance is a function of tire pressure, normal force, and velocity.
ISO 28580	Method specified in ISO 28580:2018, Passenger car, truck and bus tyre rolling resistance measurement method — Single point test and correlation of measurement results.
Magic Formula	Magic formula equations from 4.E70 in Tire and Vehicle Dynamics. The magic formula is an empirical equation based on fitting coefficients.
Mapped torque	Lookup table that is a function of the normal force and spin axis longitudinal velocity.

Dependencies

Selecting	Parameters
Pressure and velocity	Velocity independent force coefficient, aMy Linear velocity force component, bMy Quadratic velocity force component, cMy Tire pressure exponent, alphaMy Normal force exponent, betaMy
ISO 28580	Parasitic losses force, Fpl Rolling resistance constant, Cr Thermal correction factor, Kt Measured temperature, Tmeas Parasitic losses force, Fpl Ambient temperature, Tamb
Magic Formula	Rolling resistance torque coefficient, QSY Longitudinal force rolling resistance coefficient, QSY2 Linear rotational speed rolling resistance coefficient, QSY3 Quartic rotational speed rolling resistance coefficient, QSY4 Camber squared rolling resistance torque, QSY5 Load based camber squared rolling resistance torque, QSY6 Normal load rolling resistance coefficient, QSY7 Pressure load rolling resistance coefficient, QSY8 Rolling resistance scaling factor, lam_My
Mapped torque	Spin axis velocity breakpoints, VxMy Normal force breakpoints, FzMy Rolling resistance torque map, MyMap

Vertical Motion — Select type

None (default) | Mapped stiffness and damping

To calculate vertical motion, specify one of these Vertical Motion parameters.

Setting	Block Implementation
None	Block passes the applied chassis forces directly through to the rolling resistance and longitudinal force calculations.
Mapped stiffness and damping	Vertical motion depends on wheel stiffness and damping. Stiffness is a function of tire sidewall displacement and pressure. Damping is a function of tire sidewall velocity and pressure.

Selecting	Enables These Parameters
Mapped stiffness and damping	Wheel mass, MASS Initial tire displacement, zo Initial velocity, zdoto Initial wheel vertical velocity (wheel fixed frame), zdoto Vertical deflection breakpoints, zFz Pressure breakpoints, pFz Force due to deflection, Fzz Vertical velocity breakpoints, zdotFz Force due to velocity, Fzzdot

Longitudinal and Lateral

Longitudinal stiffness, Ckappa — Longitudinal stiffness

1e7 (default) | scalar

Longitudinal stiffness, C_κ, in N.

Lateral stiffness per slip angle, Calpha — Lateral stiffness

4.5e4 (default) | scalar

Lateral stiffness per slip angle, C_α, in N/rad.

Camber stiffness, Cgamma — Camber stiffness

1e3 (default) | scalar

Camber stiffness, C_ɣ, in N/rad.

Kinematic friction, muMin — Friction

.8 (default) | scalar

Kinematic friction, μ_k, dimensionless.

Static friction, muMax — Friction

1 (default) | scalar

Static friction, μ_s, dimensionless.

Longitudinal relaxation length, Lrelx — Length

.05 (default) | scalar

Longitudinal relaxation length, L_relx, in m.

Lateral relaxation length, Lrely — Length

.15 (default) | scalar

Lateral relaxation length, L_rely, in m/rad.

Rolling

Rotational damping, br — Damping

scalar

Rotational damping, br, in N·m·s/rad.

Rotational inertia (rolling axis), IYY — Inertia

scalar

Rotational inertia (rolling axis), IYY, in kg·m^2.

Initial rotational velocity, omegao — Velocity

scalar

Initial rotational velocity, omegao, in rad/s.

Unloaded radius, UNLOADED_RADIUS — Radius

0.309384029954441 (default) | scalar

Unloaded radius, in m.

Pressure and Velocity

Velocity independent force coefficient, aMy — Force coefficient

8e-4 (default) | scalar

Velocity-independent force coefficient, a, in s/m.

Dependencies

To create this parameter, select the Rolling Resistance parameter Pressure and velocity.

Linear velocity force component, bMy — Force component

.001 (default) | scalar

Linear velocity force component, b, in s/m.

Dependencies

To create this parameter, select the Rolling Resistance parameter Pressure and velocity.

Quadratic velocity force component, cMy — Force component

1.6e-4 (default) | scalar

Quadratic velocity force component, c, in s^2/m^2.

Dependencies

To create this parameter, select the Rolling Resistance parameter Pressure and velocity.

Tire pressure exponent, alphaMy — Pressure exponent

-0.003 (default) | scalar

Tire pressure exponent, ɑ, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Pressure and velocity.

Normal force exponent, betaMy — Force exponent

0.97 (default) | scalar

Normal force exponent, β, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Pressure and velocity.

ISO 28580

Parasitic losses force, Fpl — Force loss

10 (default) | scalar

Parasitic force loss, F_pl, in N.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

Rolling resistance constant, Cr — Constant

1e-3 (default) | scalar

Rolling resistance constant, C_r, in N/kN. ISO 28580 specifies the rolling resistance unit as one newton of tractive resistance for every kilonewtons of normal load.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

Thermal correction factor, Kt — Correction factor

.008 (default) | scalar

Thermal correction factor, K_t, in 1/degC.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

Measured temperature, Tmeas — Temperature

298.15 (default) | scalar

Measured temperature, T_meas, in K.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

Ambient temperature, Tamb — Temperature

298.15 (default) | scalar

Measured temperature, T_amb, in K.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

Input ambient temperature — Selection

off (default) | on

Select to create input port Tamb.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

Magic Formula

Rolling resistance torque coefficient, QSY1 — Torque coefficient

0.007 (default) | scalar

Rolling resistance torque coefficient, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Longitudinal force rolling resistance coefficient, QSY2 — Force resistance coefficient

0 (default) | scalar

Longitudinal force rolling resistance coefficient, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Linear rotational speed rolling resistance coefficient, QSY3 — Linear speed coefficient

0.0015 (default) | scalar

Linear rotational speed rolling resistance coefficient, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Quartic rotational speed rolling resistance coefficient, QSY4 — Quartic speed coefficient

8.5e-05 (default) | scalar

Quartic rotational speed rolling resistance coefficient, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Camber squared rolling resistance torque, QSY5 — Camber resistance torque

0 (default) | scalar

Camber squared rolling resistance torque, in 1/rad^2.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Load based camber squared rolling resistance torque, QSY6 — Load resistance torque

0 (default) | scalar

Load based camber squared rolling resistance torque, in 1/rad^2.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Normal load rolling resistance coefficient, QSY7 — Normal resistance coefficient

0.9 (default) | scalar

Normal load rolling resistance coefficient, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Pressure load rolling resistance coefficient, QSY8 — Pressure resistance coefficient

-0.4 (default) | scalar

Pressure load rolling resistance coefficient, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Rolling resistance scaling factor, lam_My — Scale

1 (default) | scalar

Rolling resistance scaling factor, dimensionless.

Dependencies

To create this parameter, select the Rolling Resistance parameter Magic Formula.

Mapped

Spin axis velocity breakpoints, VxMy — Breakpoints

-20:1:20 (default) | vector

Spin axis velocity breakpoints, in m/s.

Dependencies

To create this parameter, select the Rolling Resistance parameter Mapped torque.

Normal force breakpoints, FzMy — Breakpoints

0:200:1e4 (default) | vector

Normal force breakpoints, in N.

Dependencies

To create this parameter, select the Rolling Resistance parameter Mapped torque.

Rolling resistance torque map, MyMap — Lookup table

array

Rolling resistance torque versus axle speed and normal force, in N·m.

Dependencies

To create this parameter, select the Rolling Resistance parameter Mapped torque.

Aligning

Wheel width, WIDTH — Width

scalar

Wheel width, WIDTH, in m.

Linear yaw rate resistance, bMz — Resistance

0 | scalar

Linear yaw rate resistance, b_Mz, in N·m·s/rad.

Brake

Static friction coefficient, mu_static — Static friction

.3 (default) | scalar

Static friction coefficient, dimensionless.

Dependencies

To enable this parameter, for the Brake Type parameter, specify one of these types:

• Disc

• Drum

• Mapped

Kinetic friction coefficient, mu_kinetic — Kinetic friction

.2 (default) | scalar

Kinematic friction coefficient, dimensionless.

Dependencies

To enable this parameter, for the Brake Type parameter, specify one of these types:

• Disc

• Drum

• Mapped

Disc

Disc brake actuator bore, disc_abore — Bore distance

.05 (default) | scalar

Disc brake actuator bore, in m.

Dependencies

To enable the disc brake parameters, select Disc for the Brake Type parameter.

Brake pad mean radius, Rm — Radius

.177 (default) | scalar

Brake pad mean radius, in m.

Dependencies

To enable the disc brake parameters, select Disc for the Brake Type parameter.

Number of brake pads, num_pads — Count

2 (default) | scalar

Number of brake pads.

Dependencies

To enable the disc brake parameters, select Disc for the Brake Type parameter.

Drum

Drum brake actuator bore, disc_abore — Bore distance

0.0508 (default) | scalar

Drum brake actuator bore, in m.

Dependencies

To enable the drum brake parameters, select Drum for the Brake Type parameter.

Shoe pin to drum center distance, drum_a — Distance

0.123 (default) | scalar

Shoe pin to drum center distance, in m.

Dependencies

To enable the drum brake parameters, select Drum for the Brake Type parameter.

Shoe pin center to force application point distance, drum_c — Distance

0.212 (default) | scalar

Shoe pin center to force application point distance, in m.

Dependencies

To enable the drum brake parameters, select Drum for the Brake Type parameter.

Drum internal radius, drum_r — Radius

0.15 (default) | scalar

Drum internal radius, in m.

Dependencies

To enable the drum brake parameters, select Drum for the Brake Type parameter.

Shoe pin to pad start angle, drum_theta1 — Angle

0 (default) | scalar

Shoe pin to pad start angle, in deg.

Dependencies

To enable the drum brake parameters, select Drum for the Brake Type parameter.

Shoe pin to pad end angle, drum_theta2 — Angle

126 (default) | scalar

Shoe pin to pad end angle, in deg.

Dependencies

To enable the drum brake parameters, select Drum for the Brake Type parameter.

Mapped

Brake actuator pressure breakpoints, brake_p_bpt — Breakpoints

vector

Brake actuator pressure breakpoints, in bar.

Dependencies

To enable the mapped brake parameters, select Mapped for the Brake Type parameter.

Wheel speed breakpoints, brake_n_bpt — Breakpoints

vector

Wheel speed breakpoints, in rpm.

Dependencies

To enable the mapped brake parameters, select Mapped for the Brake Type parameter.

Brake torque map, f_brake_t — Lookup table

array

The lookup table for the brake torque, $f_{brake}^{}(P,N)$, is a function of applied brake pressure and wheel speed, where:

• T is brake torque, in N·m.

• P is applied brake pressure, in bar.

• N is wheel speed, in rpm.

Dependencies

To enable the mapped brake parameters, select Mapped for the Brake Type parameter.

Vertical

Wheel mass, m — Mass

9.46491996974568 (default) | scalar

Wheel mass, in kg. Used in the vertical motion calculations.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Initial tire deflection, zo — Deflection

0 (default) | scalar

Initial axle displacement along wheel-fixed z-axis, in m.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Initial wheel vertical velocity (wheel fixed frame), zdoto — Velocity

0 (default) | scalar

Initial axle velocity along wheel-fixed z-axis, in m.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Gravitational acceleration, GRAVITY — Gravity

-9.81 (default) | scalar

Gravitational acceleration, in m/s^2.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Mapped Stiffness and Damping

Vertical deflection breakpoints, zFz — Breakpoints

[0 .01 .1] (default) | vector

Vector of sidewall deflection breakpoints corresponding to the force table, in m.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Pressure breakpoints, pFz — Breakpoints

[10000 1000000] (default) | vector

Vector of pressure data points corresponding to the force table, in Pa.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Force due to deflection, Fzz — Force

[0 1e3 1e4; 0 1e4 1e5] (default) | vector

Force due to sidewall deflection and pressure along wheel-fixed z-axis, in N.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Vertical velocity breakpoints, zdotFz — Breakpoints

[-20 0 20] (default) | scalar

Vector of sidewall velocity breakpoints corresponding to the force due to velocity table, in m.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Force due to velocity, Fzzdot — Force

[500 0 -500;250 0 -250] (default) | array

Force due to sidewall velocity and pressure along wheel-fixed z-axis, in N.

Dependencies

To enable this parameter, set Vertical Motion to Mapped stiffness and damping.

Simulation

Maximum normal force, FZMAX — Force

10000 (default) | scalar

Maximum normal force, in N. Used with all vertical force calculations.

Minimum normal force, FZMIN — Force

0 (default) | scalar

Minimum normal force, in N. Used with all vertical force calculations.

Maximum pressure, PRESMAX — Pressure

scalar

Maximum pressure, PRESMAX, in Pa.

Minimum pressure, PRESMIN — Pressure

scalar

Minimum pressure, PRESMIN, in Pa.

Max allowable slip ratio (absolute), KPUMAX — Ratio

scalar

Max allowable slip ratio (absolute), KPUMAX, dimensionless.

Minimum allowable slip ratio (absolute), KPUMIN — Ratio

scalar

Minimum allowable slip ratio (absolute), KPUMIN, dimensionless.

Max allowable slip angle (absolute), ALPMAX — Angle

scalar

Max allowable slip angle (absolute), ALPMAX, in rad.

Minimum allowable slip angle (absolute), ALPMIN — Angle

scalar

Minimum allowable slip angle (absolute), ALPMIN, in rad.

Maximum allowable camber angle, CAMMAX — Angle

scalar

Maximum allowable camber angle CAMMAX, in rad.

Minimum allowable camber angle, CAMMIN — Angle

scalar

Minimum allowable camber angle, CAMMIN, in rad.

Minimum ambient temperature, TMIN — Tmin

0 (default) | scalar

Minimum ambient temperature, T_MIN, in K.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

Maximum ambient temperature, TMAX — Tmax

400 (default) | scalar

Maximum ambient temperature, T_MAX, in K.

Dependencies

To create this parameter, select the Rolling Resistance parameter ISO 28580.

References

[1] Fiala, E. "Seitenkrafte am Rollenden Luftreifen." VDI Zeitschrift, V.D.I.. Vol 96, 1954.

[2] Highway Tire Committee. Stepwise Coastdown Methodology for Measuring Tire Rolling Resistance. Standard J2452_199906. Warrendale, PA: SAE International, June 1999.

[3] ISO 28580:2018. Passenger car, truck and bus tyre rolling resistance measurement method — Single point test and correlation of measurement results. ISO (International Organization for Standardization), 2018.

[4] Pacejka, H. B. Tire and Vehicle Dynamics. 3rd ed. Oxford, UK: SAE and Butterworth-Heinemann, 2012.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.