2-D Continuous Wavelet Transform
The 2-D continuous wavelet transform (CWT) is a representation of 2-D data (image data) in four variables: dilation, rotation, and position. Dilation and rotation are real-valued scalars and position is a 2-D vector with real-valued elements. Let x denote a two-element vector of real-numbers. If
is square-integrable on the plane, the 2-D CWT is defined as
where the bar denotes the complex conjugate and rθ is the 2-D rotation matrix
The 2-D CWT is a space-scale representation of an image. You can view the inverse of the scale and the rotation angle taken together as a spatial-frequency variable, which gives the 2-D CWT an interpretation as a space-frequency representation.
For all admissible 2-D wavelets, the 2-D CWT acts as a local filter for an image in scale and position. If the wavelet is isotropic, there is no dependence on angle in the analysis. The Mexican hat wavelet, also known as the Ricker wavelet, is an example of an isotropic wavelet. Isotropic wavelets are suitable for pointwise analysis of images. If the wavelet is anisotropic, there is a dependence on angle in the analysis, and the 2-D CWT acts a local filter for an image in scale, position, and angle. The Cauchy wavelet is an example of an anisotropic wavelet. In the Fourier domain, this means that the spatial frequency support of the wavelet is a convex cone with the apex at the origin. Anisotropic wavelets are suitable for detecting directional features in an image.
You can use the Wavelet Image Analyzer app to visualize the continuous wavelet decomposition of images. With the app, you can export the decompositions to your workspace, as well as generate scripts to reproduce results.
Obtain 2-D CWT of Image Using Isotropic and Anisotropic Wavelets
Load an image.
imdata = imread("triangle.jpg");
imagesc(imdata)
Isotropic Wavelet
Specify an isotropic wavelet and obtain the 2-D CWT of the image at scales 2, 4, and 8 and angles 0, , , and .
wav = "mexh"; sca = [2 4 8]; rot = [0 1 2 3]*(pi/6); imdata_CWT = cwtft2(imdata,Wavelet=wav,Scales=sca, ... Angles=rot);
Display the magnitudes of the coefficients at all scales and angles. Use the helper function helperPlot2DCWT. Because the wavelet is isotropic, there is no dependence on angle in the analysis. Isotropic wavelets are suitable for pointwise analysis of images.
cfs = imdata_CWT.cfs;
figure(Position=[0 0 560 700])
helperPlot2DCWT(cfs,"Isotropic Wavelet")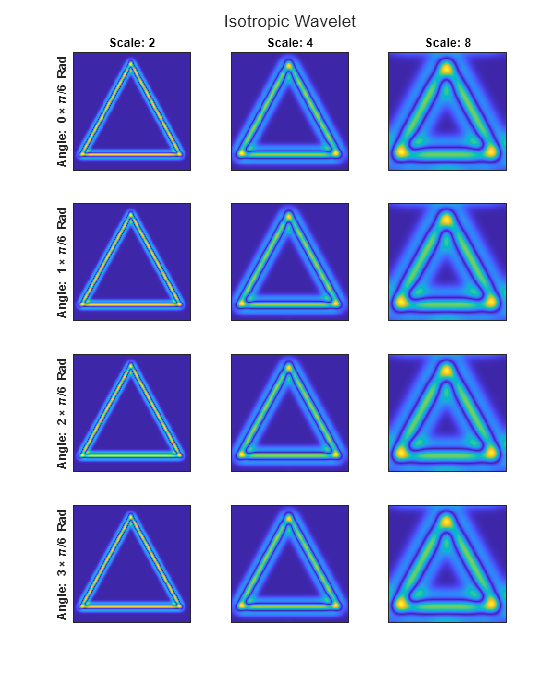
Anisotropic Wavelet
Obtain the 2-D CWT of the image at the same scales and angles, but this time specify an anisotropic wavelet.
wav = "morlet"; sca = [2 4 8]; rot = [0 1 2 3]*(pi/6); imdata_CWT = cwtft2(imdata,Wavelet=wav,Scales=sca, ... Angles=rot);
Display the magnitudes of the coefficients at all scales and angles. Because the wavelet is anisotropic, there is a dependence on angle in the analysis. Anisotropic wavelets are suitable for detecting directional features in an image.
cfs = imdata_CWT.cfs;
figure(Position=[0 0 560 700])
helperPlot2DCWT(cfs,"Anisotropic Wavelet")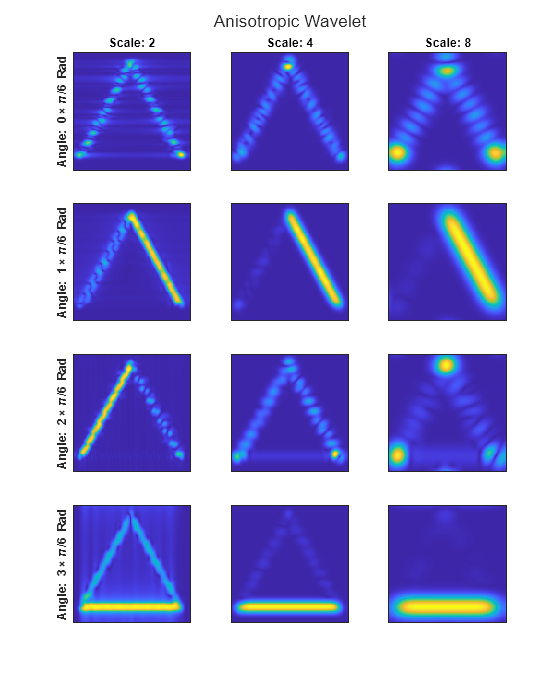
Helper Function
function helperPlot2DCWT(cfs,str) % This function is only intended to support this Wavelet example. % It may change or be removed in a future release. t=tiledlayout(4,3); for i=1:4 for j=1:3 nexttile imagesc(abs(cfs(:,:,1,j,i))) if j==1 ylabel("Angle: "+num2str(i-1)+"\times\pi/6 Rad", ... FontWeight="bold"); end if i==1 title("Scale: "+num2str(2^j)); end xticks([]) yticks([]) end end title(t,str) end