Remove Time-Localized Frequency Components
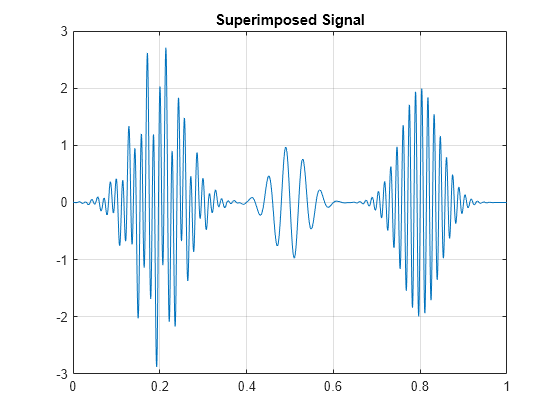
Create a signal consisting of exponentially weighted sine waves. The signal has two 25-Hz components -- one centered at 0.2 seconds and one centered at 0.5 seconds. It also has two 70-Hz components -- one centered at 0.2 and one centered at 0.8 seconds. The first 25-Hz and 70-Hz components co-occur in time.
t = 0:1/2000:1-1/2000; dt = 1/2000; x1 = sin(50*pi*t).*exp(-50*pi*(t-0.2).^2); x2 = sin(50*pi*t).*exp(-100*pi*(t-0.5).^2); x3 = 2*cos(140*pi*t).*exp(-50*pi*(t-0.2).^2); x4 = 2*sin(140*pi*t).*exp(-80*pi*(t-0.8).^2); x = x1+x2+x3+x4; plot(t,x) grid on; title('Superimposed Signal')
Obtain and display the CWT.
cwt(x,2000);
title('Analytic CWT using Default Morse Wavelet');
Remove the 25 Hz component which occurs from approximately 0.07 to 0.3 seconds by zeroing out the CWT coefficients. Use the inverse CWT (icwt) to reconstruct an approximation to the signal.
[cfs,f] = cwt(x,2000); T1 = .07; T2 = .33; F1 = 19; F2 = 34; cfs(f > F1 & f < F2, t> T1 & t < T2) = 0; xrec = icwt(cfs);
Display the CWT of the reconstructed signal. The initial 25-Hz component is removed.
cwt(xrec,2000)
Plot the original signal and the reconstruction.
subplot(2,1,1); plot(t,x); grid on; title('Original Signal'); subplot(2,1,2); plot(t,xrec) grid on; title('Signal with first 25-Hz component removed');

Compare the reconstructed signal with the original signal without the 25-Hz component centered at 0.2 seconds.
y = x2+x3+x4; figure; plot(t,xrec) hold on plot(t,y,'r--') grid on; legend('Inverse CWT approximation','Original Signal Without 25-Hz'); hold off
