compand
Source coding mu-law or A-law compressor or expander
Description
out = compand(in,param,v)param input
specifies the mu-law compression value and must be set to a mu value for mu-law compressor
computation (a mu-law value of 255 is used in practice). v specifies
the peak magnitude of the input data sequence.
out = compand(in,param,v,method)param specifies the mu-law compander or A-law compander value (a
mu-law value of 255 and an A-law value of 87.6 are used in practice).
method specifies the type of compressor or expander computation for
the function to perform on the input data sequence.
Examples
Input Arguments
Output Arguments
Algorithms
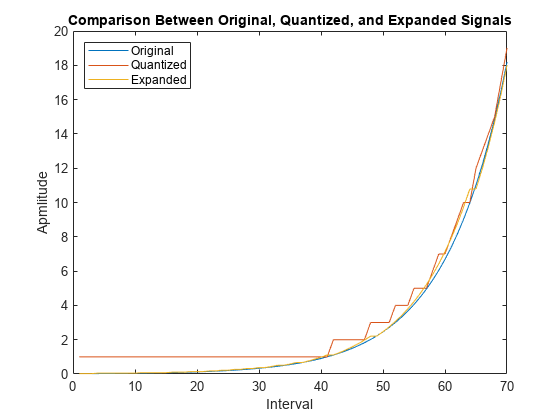
In certain applications, such as speech processing, using a logarithmic computation (called a compressor) before quantizing the input data is common. The inverse operation of a compressor is called an expander. The combination of a compressor and expander is called a compander.
For a given signal, x, the output of the (µ-law) compressor is
µ is the µ-law parameter of the compander, log is
the natural logarithm, and sgn is the signum function (sign in MATLAB®).
µ-law expansion for input signal x is given by the inverse function y-1,
For a given signal, x, the output of the (A-law) compressor is
A is the A-law parameter of the compander, log is
the natural logarithm, and sgn is the signum function (sign in MATLAB).
A-law expansion for input signal x is given by the inverse function y-1,
References
[1] Sklar, Bernard. Digital Communications: Fundamentals and Applications. Englewood Cliffs, NJ: Prentice-Hall, 1988.
Version History
Introduced before R2006a