lqi

Contrôle linéaire quadratique intégral

Syntaxe

[K,S,e] = lqi(SYS,Q,R,N)


Description

lqi calcule une loi de système d’asservissement d'état pour la boucle de suivi illustrée à la figure suivante.

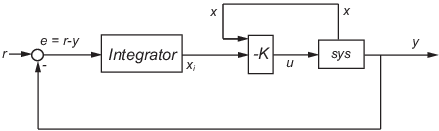
Pour un système physique sys avec équations de représentation d'état (ou leur équivalent discret) :

$$\begin{array}{l}\frac{dx}{dt}=Ax+Bu\\ y=Cx+Du\end{array}$$

le système d’asservissement d'état présente la forme

$$u=-K[x;x_i]$$

où x_i correspond à la sortie de l'intégrateur. Cette loi de contrôle assure que la sortie y suit la commande de référence r. Pour les systèmes MIMO, le nombre d'intégrateurs équivaut à la dimension de la sortie y.

[K,S,e] = lqi(SYS,Q,R,N) calcule la matrice de gain optimale K avec un modèle de représentation d’état SYS pour le système physique et des matrices de pondération Q, R, N. La loi de contrôle u = -Kz = -K[x;x_i] minimise les fonctions de coût suivantes (pour r = 0)

• $$J(u)={\displaystyle {\int }_0^{\infty }\{z^{T}Qz+u^{T}Ru+2z^{T}Nu\}dt}$$ pour le temps continu

• $$J(u)={\displaystyle \sum _{n=0}^{\infty }\{z^{T}Qz+u^{T}Ru+2z^{T}Nu\}}$$ pour le temps discret

En temps discret, lqi calcule la sortie de l'intégrateur x_i au moyen de la formule d'Euler

$$x_i[n+1]=x_i[n]+Ts(r[n]-y[n])$$

où Ts correspond au pas d'échantillonnage de SYS.

Lorsque vous omettez la matrice N, N est réglé sur 0. lqi renvoie la solution S de l'équation algébrique de Riccati associée et les valeurs propres en boucle fermée e.

Limitations

Pour le système de représentation d'état suivant avec un système physique à intégrateur augmenté :

$$\begin{array}{l}\frac{\delta z}{\delta t}=A_{a}z+B_{a}u\\ y=C_{a}z+D_{a}u\end{array}$$

Les données relatives au problème doivent répondre remplir les conditions suivantes :

• La paire (A, B) doit pouvoir être stabilisée.

• R doit être un nombre défini positif.

• $$\left[\begin{array}{cc}Q& N\\ N^T& R\end{array}\right]$$ doit être un nombre semi-défini positif (de manière équivalente, $$Q-N{R}^{-1}{N}^T\ge 0$$).

• $$\left(Q-N{R}^{-1}{N}^T,A_a-B_a{R}^{-1}{N}^T\right)$$ ne doit pas présenter de mode non détectable sur l’axe imaginaire (ou le cercle unitaire en temps discret).

Conseils

lqi prend en charge les modèles de descripteur avec E non singulier. La sortie S de lqi correspond à la solution de l'équation de Riccati pour le modèle de représentation d’état explicite équivalent

$$\frac{dx}{dt}=E^{-1}Ax+E^{-1}Bu$$

Références

[1] P. C. Young and J. C. Willems, "An approach to the linear multivariable servomechanism problem", International Journal of Control, Volume 15, Issue 5, May 1972 , pages 961–979.

Historique des versions

Introduit dans R2008b

Voir aussi

lqr | lqgreg | lqgtrack | lqg | care | dare