La traduction de cette page n'est pas à jour. Cliquez ici pour voir la dernière version en anglais.

lqr

Design d'un régulateur linéaire quadratique (LQR, Linear Quadratic Regulator)

Syntaxe

[K,S,P] = lqr(sys,Q,R,N)

[K,S,P] = lqr(A,B,Q,R,N)

Description

[K,S,P] = lqr(sys,Q,R,N) calcule la matrice de gain optimal K, la solution S de l'équation algébrique de Riccati associée et les pôles en boucle fermée P pour le modèle de représentation d’état en temps continu ou en temps discret sys. Q et R sont respectivement les matrices de poids des états et des entrées. Lorsque la matrice des termes croisés N est omise, elle est définie sur zéro.

[K,S,P] = lqr(A,B,Q,R,N) calcule la matrice de gain optimal K, la solution S de l'équation algébrique de Riccati associée et les pôles en boucle fermée P au moyen des matrices de représentation d’état en temps continu A et B. Cette syntaxe n’est valide que pour les modèles en temps continu. Pour les modèles en temps discret, utilisez dlqr.

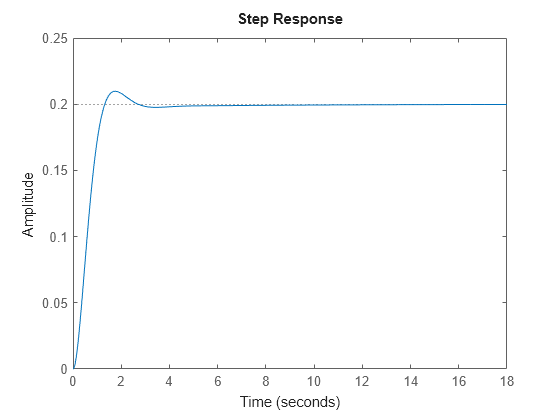
Exemples

Contrôle LQR pour un modèle de pendule inversé

pendulumModelCart.mat contient le modèle de représentation d'état d'un pendule inversé sur un chariot où les sorties correspondent au déplacement du chariot x et à l'angle du pendule $\theta$. L’entrée de contrôle u correspond à la force horizontale exercée sur le chariot.

$$\begin{array}{l}\left[\begin{array}{c}\underset{}{\overset{\dot{}}{x}}\\ \underset{}{\overset{¨}{x}}\\ \underset{}{\overset{\dot{}}{\theta }}\\ \underset{}{\overset{¨}{\theta }}\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -0.1& 3& 0\\ 0& 0& 0& 1\\ 0& -0.5& 30& 0\end{array}\right]\left[\begin{array}{c}x\\ \underset{}{\overset{\dot{}}{x}}\\ \theta \\ \underset{}{\overset{\dot{}}{\theta }}\end{array}\right]+\left[\begin{array}{c}0\\ 2\\ 0\\ 5\end{array}\right]u\\ y=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}x\\ \underset{}{\overset{\dot{}}{x}}\\ \theta \\ \underset{}{\overset{\dot{}}{\theta }}\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]u\end{array}$$

Commencez par charger le modèle de représentation d’état sys dans l’espace de travail.

load('pendulumCartModel.mat','sys')

Étant donné que les sorties correspondent à x et à $\theta$, et qu’il n’existe qu’une entrée, utilisez la règle de Bryson pour déterminer Q et R.

Q = [1,0,0,0;...
    0,0,0,0;...
    0,0,1,0;...
    0,0,0,0];
R = 1;

Trouvez la matrice de gain K au moyen de lqr. Étant donné que N n’est pas spécifié, lqr définit N sur 0.

[K,S,P] = lqr(sys,Q,R)

K = 1×4

   -1.0000   -1.7559   16.9145    3.2274

S = 4×4

    1.5346    1.2127   -3.2274   -0.6851
    1.2127    1.5321   -4.5626   -0.9640
   -3.2274   -4.5626   26.5487    5.2079
   -0.6851   -0.9640    5.2079    1.0311

P = 4×1 complex

  -0.8684 + 0.8523i
  -0.8684 - 0.8523i
  -5.4941 + 0.4564i
  -5.4941 - 0.4564i

Même si la règle de Bryson permet généralement d’obtenir des résultats satisfaisants, elle ne constitue souvent que le point de départ d'une procédure de design itérative par approximations successives visant à régler la réponse de votre système en boucle fermée en fonction des exigences de design.

Contrôle LQR au moyen des matrices de représentation d’état

aircraftPitchModel.mat contient les matrices de représentation d’état d'un avion où l'entrée correspond à l'angle de déviation de la gouverne de profondeur $\delta$ et la sortie, à l'angle de tangage de l'avion $\theta$.

$$\begin{array}{l}\left[\begin{array}{c}\underset{}{\overset{\dot{}}{\alpha }}\\ \underset{}{\overset{\dot{}}{q}}\\ \underset{}{\overset{\dot{}}{\theta }}\end{array}\right]=\left[\begin{array}{ccc}-0.313& 56.7& 0\\ -0.0139& -0.426& 0\\ 0& 56.7& 0\end{array}\right]\left[\begin{array}{c}\alpha \\ q\\ \theta \end{array}\right]+\left[\begin{array}{c}0.232\\ 0.0203\\ 0\end{array}\right]\left[\delta \right]\\ y=\left[\begin{array}{ccc}0& 0& 1\end{array}\right]\left[\begin{array}{c}\alpha \\ q\\ \theta \end{array}\right]+\left[0\right]\left[\delta \right]\end{array}$$

Pour une référence indicielle de 0,2 radian, tenez compte des critères de design suivants :

• Temps de montée inférieur à 2 secondes

• Temps de stabilisation inférieur à 10 secondes

• Erreur d’état stationnaire inférieur à 2 %

Chargez les données du modèle dans l’espace de travail.

load('aircraftPitchModel.mat')

Définissez la matrice pondérée état/coût Q et la matrice pondérée de contrôle R. En règle générale, vous pouvez utiliser la règle de Bryson pour définir vos matrices pondérées initiales Q et R. Pour cet exemple, considérons le vecteur de sortie C avec un facteur de mise à l’échelle de 2 pour la matrice Q et choisissons R en tant que 1. R est un scalaire étant donné que le système ne présente qu’une entrée.

R = 1

R = 1

Q1 = 2*C'*C

Q1 = 3×3

     0     0     0
     0     0     0
     0     0     2

Calculez la matrice de gain au moyen de lqr.

[K1,S1,P1] = lqr(A,B,Q1,R);

Vérifiez la réponse indicielle en boucle fermée par rapport à la matrice de gain générée K1.

sys1 = ss(A-B*K1,B,C,D);
step(sys1)

Étant donné que cette réponse ne satisfait pas aux objectifs de design, augmentez le facteur de mise à l’échelle à 25, calculez la matrice de gain K2 et vérifiez la réponse indicielle en boucle fermée pour la matrice de gain K2.

Q2 = 25*C'*C

Q2 = 3×3

     0     0     0
     0     0     0
     0     0    25

[K2,S2,P2] = lqr(A,B,Q2,R);
sys2 = ss(A-B*K2,B,C,D);
step(sys2)

Dans la réponse indicielle en boucle fermée, les temps de montée et de stabilisation, et l’erreur d’état stationnaire satisfont aux objectifs de design.

Arguments d'entrée

sys — Modèle de systèmes dynamiques

Objet de modèle ss

Modèle de systèmes dynamiques indiqué en tant qu’objet de modèle ss.

A — Matrice d'état

Matrice n par n

Matrice d'état spécifiée en tant que matrice n par n où n désigne le nombre d’états.

B — Matrice entrée-état

Matrice n par m

Matrice entrée/état spécifiée en tant que matrice entrée/état n par m où m désigne le nombre d’entrées.

Q — Matrice pondérée état/coût

matrice

Matrice pondérée état/coût spécifiée en tant que matrice n par n où n désigne le nombre d’états. Vous pouvez utiliser la règle de Bryson pour définir les valeurs initiales de Q attribuées par :

$$\begin{array}{l}{Q}_{i,i}=\frac{1}{\text{maximum acceptable value of }{\left(erro{r}_{states}\right)}^2},\text{ i}\in \left\{1,2,\mathrm{...},n\right\}\\ Q=\left[\begin{array}{cccc}{Q}_{1,1}& 0& \cdots & 0\\ 0& Q_{2,2}& \cdots & 0\\ 0& 0& \ddots & ⋮\\ 0& 0& \cdots & Q_{n,n}\end{array}\right]\end{array}$$

. Ici, n désigne le nombre d’états.

R — Matrice pondérée entrée/coût

scalaire | matrice

Matrice pondérée entrée/coût spécifiée en tant que scalaire ou que matrice de même taille que D'D. Ici, D désigne le flux qui alimente la matrice de représentation d’état. Vous pouvez utiliser la règle de Bryson pour définir les valeurs initiales de R attribuées par :

$$\begin{array}{l}{R}_{j,j}=\frac{1}{\text{maximum acceptable value of }{\left(erro{r}_{inputs}\right)}^2},\text{ j}\in \left\{1,2,\mathrm{...},m\right\}\\ R=\left[\begin{array}{cccc}{R}_{1,1}& 0& \cdots & 0\\ 0& R_{2,2}& \cdots & 0\\ 0& 0& \ddots & ⋮\\ 0& 0& \cdots & R_{m,m}\end{array}\right]\end{array}$$

. Ici, m désigne le nombre d’entrées.

N — Matrice des termes croisées facultative

0 (par défaut) | matrice

Matrice des termes croisées spécifiée en tant que matrice. Si N n’est pas spécifié, lqr définit N sur 0 par défaut.

Arguments en sortie

K — Gain optimal

vecteur ligne

Gain optimal du système en boucle fermée, renvoyé en tant que vecteur ligne de taille n, où n désigne le nombre d’états.

S — Solution de l'équation algébrique de Riccati associée

matrice

Solution de l'équation algébrique de Riccati associée renvoyée en tant que matrice n par n, où n désigne le nombre d’états. Autrement dit, S correspond à la même dimension que la matrice de représentation d’état A. Pour plus d’informations, consultez icare et idare.

P — Pôles du système en boucle fermée

vecteur colonne

Pôles du système en boucle fermée, renvoyés en tant que vecteur colonne de taille n, où n désigne le nombre d’états.

Limitations

Les données d’entrée doivent remplir les conditions suivantes :

• La paire A et B doit pouvoir être stabilisée.

• [Q,N;N',R] doit être un nombre défini non négatif.

• R>0 et $$Q-N{R}^{-1}{N}^T\ge 0$$.

• ($$(Q-N{R}^{-1}{N}^T,A-B{R}^{-1}{N}^T)$$ ne présente aucun mode non détectable sur l’axe imaginaire (ou le cercle unitaire en temps discret).

Conseils

• lqr prend en charge les modèles de descripteur avec E non singulier. La sortie S de lqr correspond à la solution de l'équation algébrique de Riccati pour le modèle de représentation d’état explicite équivalent :

  $$\frac{dx}{dt}=E^{-1}Ax+E^{-1}Bu$$

Algorithmes

Pour les systèmes en temps continu, lqr calcule le système d’avertissement d’état $$u=-Kx$$ qui minimise la fonction de coût quadratique

$$J(u)={\displaystyle {\int }_0^{\infty }(x^{T}Qx+u^{T}Ru+2x^{T}Nu)dt}$$

soumis à la dynamique du système $$\dot{x}=Ax+Bu$$.

Outre le gain de retour d’état K, lqr renvoie la solution S de l’équation algébrique de Riccati associée

$$A^{T}S+SA-(SB+N)R^{-1}(B^{T}S+N^T)+Q=0$$

et les pôles en boucle fermée $$P=eig\left(A-BK\right)$$. La matrice de gain K est dérivée de S au moyen de

$$K=R^{-1}(B^{T}S+N^T).$$

Pour les systèmes en temps discret, lqr calcule le système d’avertissement d’état $$u_n=-K{x}_n$$ qui minimise

$$J={\displaystyle \sum _{n=0}^{\infty }\{x^{T}Qx+u^{T}Ru+2x^{T}Nu\}}$$

soumis à la dynamique du système $$x_{n+1}=A{x}_n+B{u}_n$$.

Dans tous les cas, lorsque vous omettez la matrice des termes croisés N, lqr définit N sur 0.

Historique des versions

Introduit avant R2006a

Voir aussi

icare | idare | dlqr | lqg | lqi | lqrd | lqry | lqgreg | lqgtrack

Rubriques

• Regulate Pressure in Drum Boiler