LQG Regulation: Rolling Mill Case Study
Overview of this Case Study
This case study demonstrates the use of the LQG design tools in a process control application. The goal is to regulate the horizontal and vertical thickness of the beam produced by a hot steel rolling mill. This example is adapted from [1]. The full plant model is MIMO and the example shows the advantage of direct MIMO LQG design over separate SISO designs for each axis. Type
milldemo
at the command line to run this demonstration interactively.
Process and Disturbance Models
The rolling mill is used to shape rectangular beams of hot metal. The desired outgoing shape is sketched below.
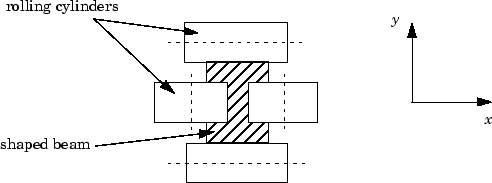
This shape is impressed by two pairs of rolling cylinders (one per axis) positioned by hydraulic actuators. The gap between the two cylinders is called the roll gap.
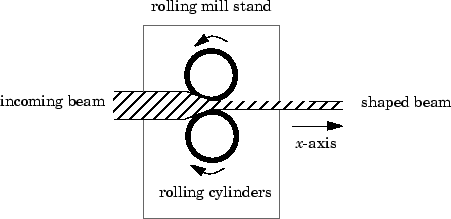
The objective is to maintain the beam thickness along the x- and y-axes within the quality assurance tolerances. Variations in output thickness can arise from the following:
Variations in the thickness/hardness of the incoming beam
Eccentricity in the rolling cylinders
Feedback control is necessary to reduce the effect of these disturbances. Because the roll gap cannot be measured close to the mill stand, the rolling force is used instead for feedback.
The input thickness disturbance is modeled as a low pass filter driven by white noise. The eccentricity disturbance is approximately periodic and its frequency is a function of the rolling speed. A reasonable model for this disturbance is a second-order bandpass filter driven by white noise.
This leads to the following generic model for each axis of the rolling process.

The measured rolling force variation f is a combination of the incremental force delivered by the hydraulic actuator and of the disturbance forces due to eccentricity and input thickness variation. Note that:
The outputs of H(s), Fe(s), and Fi(s) are the incremental forces delivered by each component.
An increase in hydraulic or eccentricity force reduces the output thickness gap δ.
An increase in input thickness increases this gap.
The model data for each axis is summarized below.
Model Data for the x-Axis
Model Data for the y-Axis
LQG Design for the x-Axis
As a first approximation, ignore the cross-coupling between the x- and y-axes and treat each axis independently. That is, design one SISO LQG regulator for each axis. The design objective is to reduce the thickness variations δx and δy due to eccentricity and input thickness disturbances.
Start with the x-axis. First specify the model components as transfer function objects.
% Hydraulic actuator (with input "u-x") Hx = tf(2.4e8,[1 72 90^2],'inputname','u-x') % Input thickness/hardness disturbance model Fix = tf(1e4,[1 0.05],'inputn','w-ix') % Rolling eccentricity model Fex = tf([3e4 0],[1 0.125 6^2],'inputn','w-ex') % Gain from force to thickness gap gx = 1e-6;
Next build the open-loop model shown in Process and Disturbance Models. You could use the function
connect for this purpose, but it is easier to build this
model by elementary append and series
connections.
% I/O map from inputs to forces f1 and f2
Px = append([ss(Hx) Fex],Fix)
% Add static gain from f1,f2 to outputs "x-gap" and "x-force"
Px = [-gx gx;1 1] * Px
% Give names to the outputs:
set(Px,'outputn',{'x-gap' 'x-force'})
Note
To obtain minimal state-space realizations, always convert transfer function models to state space before connecting them. Combining transfer functions and then converting to state space may produce nonminimal state-space models.
The variable Px now contains an open-loop state-space model
complete with input and output names.
Px.inputname
ans =
'u-x'
'w-ex'
'w-ix'
Px.outputname
ans =
'x-gap'
'x-force'
The second output 'x-force' is the rolling force measurement.
The LQG regulator will use this measurement to drive the hydraulic actuator and
reduce disturbance-induced thickness variations
δx.
The LQG design involves two steps:
The performance criterion J(ux) penalizes low and high frequencies equally. Because low-frequency variations are of primary concern, eliminate the high-frequency content of δx with the low-pass filter 30/(s + 30) and use the filtered value in the LQ performance criterion.
lpf = tf(30,[1 30])
% Connect low-pass filter to first output of Px
Pxdes = append(lpf,1) * Px
set(Pxdes,'outputn',{'x-gap*' 'x-force'})
% Design the state-feedback gain using LQRY and q=1, r=1e-4
kx = lqry(Pxdes(1,1),1,1e-4)
Note
lqry expects all inputs to be commands and all outputs to
be measurements. Here the command 'u-x' and the measurement
'x-gap*' (filtered gap) are the first input and first
output of Pxdes. Hence, use the syntax
Pxdes(1,1) to specify just the I/O relation between
'u-x' and 'x-gap*'.
Next, design the Kalman estimator with the function kalman. The
process noise
has unit covariance by construction. Set the measurement noise covariance to 1000
to limit the high frequency gain, and keep only the measured output
'x-force' for estimator design.
estx = kalman(Pxdes(2,:),eye(2),1000)
Finally, connect the state-feedback gain kx and state estimator
estx to form the LQG regulator.
Regx = lqgreg(estx,kx)
This completes the LQG design for the x−axis.
Let's look at the regulator Bode response between 0.1 and 1000 rad/sec.
h = bodeplot(Regx,{0.1 1000})
setoptions(h,'PhaseMatching','on')
The phase response has an interesting physical interpretation. First, consider an increase in input thickness. This low-frequency disturbance boosts both output thickness and rolling force. Because the regulator phase is approximately 0o at low frequencies, the feedback loop then adequately reacts by increasing the hydraulic force to offset the thickness increase. Now consider the effect of eccentricity. Eccentricity causes fluctuations in the roll gap (gap between the rolling cylinders). When the roll gap is minimal, the rolling force increases and the beam thickness diminishes. The hydraulic force must then be reduced (negative force feedback) to restore the desired thickness. This is exactly what the LQG regulator does as its phase drops to -180o near the natural frequency of the eccentricity disturbance (6 rad/sec).
Next, compare the open- and closed-loop responses from disturbance to thickness
gap. Use feedback to close the loop. To help specify the feedback
connection, look at the I/O names of the plant Px and regulator
Regx.
Px.inputname
ans =
'u-x'
'w-ex'
'w-ix'
Regx.outputname
ans =
'u-x'
Px.outputname
ans =
'x-gap'
'x-force'
Regx.inputname
ans =
'x-force'
This indicates that you must connect the first input and second output of
Px to the regulator.
clx = feedback(Px,Regx,1,2,+1) % Note: +1 for positive feedback
You are now ready to compare the open- and closed-loop Bode responses from disturbance to thickness gap.
h = bodeplot(Px(1,2:3),'--',clx(1,2:3),'-',{0.1 100})
setoptions(h,'PhaseMatching','on')
The dashed lines show the open-loop response. Note that the peak gain of the eccentricity-to-gap response and the low-frequency gain of the input-thickness-to-gap response have been reduced by about 20 dB.
Finally, use lsim to simulate the open- and closed-loop time
responses to the white noise inputs wex
and wix. Choose dt=0.01
as sample time for the simulation, and derive equivalent discrete white noise inputs
for this sampling rate.
dt = 0.01 t = 0:dt:50 % time samples % Generate unit-covariance driving noise wx = [w-ex;w-ix]. % Equivalent discrete covariance is 1/dt wx = sqrt(1/dt) * randn(2,length(t)) lsim(Px(1,2:3),':',clx(1,2:3),'-',wx,t)
Right-click on the plot that appears and select Show Input to turn off the display of the input.
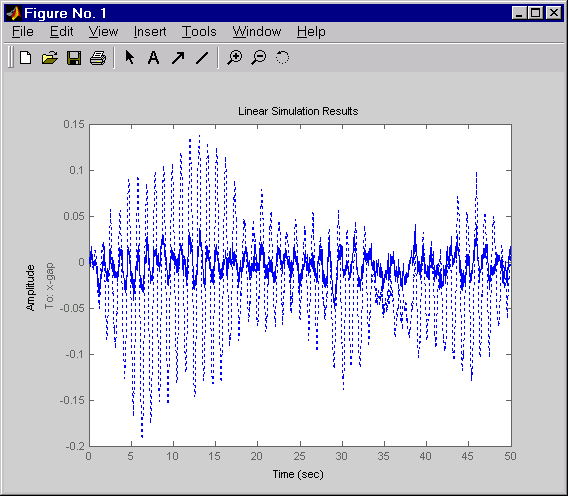
The dotted lines correspond to the open-loop response. In this simulation, the LQG regulation reduces the peak thickness variation by a factor 4.
LQG Design for the y-Axis
The LQG design for the y-axis (regulation of the y thickness) follows the exact same steps as for the x-axis.
% Specify model components
Hy = tf(7.8e8,[1 71 88^2],'inputn','u-y')
Fiy = tf(2e4,[1 0.05],'inputn','w-iy')
Fey = tf([1e5 0],[1 0.19 9.4^2],'inputn','w-ey')
gy = 0.5e-6 % force-to-gap gain
% Build open-loop model
Py = append([ss(Hy) Fey],Fiy)
Py = [-gy gy;1 1] * Py
set(Py,'outputn',{'y-gap' 'y-force'})
% State-feedback gain design
Pydes = append(lpf,1) * Py % Add low-freq. weigthing
set(Pydes,'outputn',{'y-gap*' 'y-force'})
ky = lqry(Pydes(1,1),1,1e-4)
% Kalman estimator design
esty = kalman(Pydes(2,:),eye(2),1e3)
% Form SISO LQG regulator for y-axis and close the loop
Regy = lqgreg(esty,ky)
cly = feedback(Py,Regy,1,2,+1)
Compare the open- and closed-loop response to the white noise input disturbances.
dt = 0.01 t = 0:dt:50 wy = sqrt(1/dt) * randn(2,length(t)) lsim(Py(1,2:3),':',cly(1,2:3),'-',wy,t)
Right-click on the plot that appears and select Show Input to turn off the display of the input.

The dotted lines correspond to the open-loop response. The simulation results are comparable to those for the x-axis.
Cross-Coupling Between Axes
The x/y thickness regulation, is a MIMO problem. So far you have treated each axis separately and closed one SISO loop at a time. This design is valid as long as the two axes are fairly decoupled. Unfortunately, this rolling mill process exhibits some degree of cross-coupling between axes. Physically, an increase in hydraulic force along the x-axis compresses the material, which in turn boosts the repelling force on the y-axis cylinders. The result is an increase in y-thickness and an equivalent (relative) decrease in hydraulic force along the y-axis.
The figure below shows the coupling.

Accordingly, the thickness gaps and rolling forces are related to the outputs of the x- and y-axis models by
Let's see how the previous "decoupled" LQG design fares when cross-coupling is
taken into account. To build the two-axes model, shown above, append the models
Px and Py for the x-
and y-axes.
P = append(Px,Py)
For convenience, reorder the inputs and outputs so that the commands and thickness gaps appear first.
P = P([1 3 2 4],[1 4 2 3 5 6])
P.outputname
ans =
'x-gap'
'y-gap'
'x-force'
'y-force'
Finally, place the cross-coupling matrix in series with the outputs.
gxy = 0.1; gyx = 0.4; CCmat = [eye(2) [0 gyx*gx;gxy*gy 0] ; zeros(2) [1 -gyx;-gxy 1]] Pc = CCmat * P Pc.outputname = P.outputname
To simulate the closed-loop response, also form the closed-loop model by
feedin = 1:2 % first two inputs of Pc are the commands feedout = 3:4 % last two outputs of Pc are the measurements cl = feedback(Pc,append(Regx,Regy),feedin,feedout,+1)
You are now ready to simulate the open- and closed-loop responses to the driving
white noises wx (for the x-axis) and
wy (for the y-axis).
wxy = [wx ; wy] lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)
Right-click on the plot that appears and select Show Input to turn off the display of the input.

The response reveals a severe deterioration in regulation performance along the x-axis (the peak thickness variation is about four times larger than in the simulation without cross-coupling). Hence, designing for one loop at a time is inadequate for this level of cross-coupling, and you must perform a joint-axis MIMO design to correctly handle coupling effects.
MIMO LQG Design
Start with the complete two-axis state-space model Pc
derived in Cross-Coupling Between Axes.
The model inputs and outputs are
Pc.inputname
ans =
'u-x'
'u-y'
'w-ex'
'w-ix'
'w_ey'
'w_iy'
P.outputname
ans =
'x-gap'
'y-gap'
'x-force'
'y-force'
As earlier, add low-pass filters in series with the 'x-gap' and
'y-gap' outputs to penalize only low-frequency thickness
variations.
Pdes = append(lpf,lpf,eye(2)) * Pc Pdes.outputn = Pc.outputn
Next, design the LQ gain and state estimator as before (there are now two commands and two measurements).
k = lqry(Pdes(1:2,1:2),eye(2),1e-4*eye(2)) % LQ gain est = kalman(Pdes(3:4,:),eye(4),1e3*eye(2)) % Kalman estimator RegMIMO = lqgreg(est,k) % form MIMO LQG regulator
The resulting LQG regulator RegMIMO has two inputs and two
outputs.
RegMIMO.inputname
ans =
'x-force'
'y-force'
RegMIMO.outputname
ans =
'u-x'
'u-y'
Plot its singular value response (principal gains).
sigma(RegMIMO)
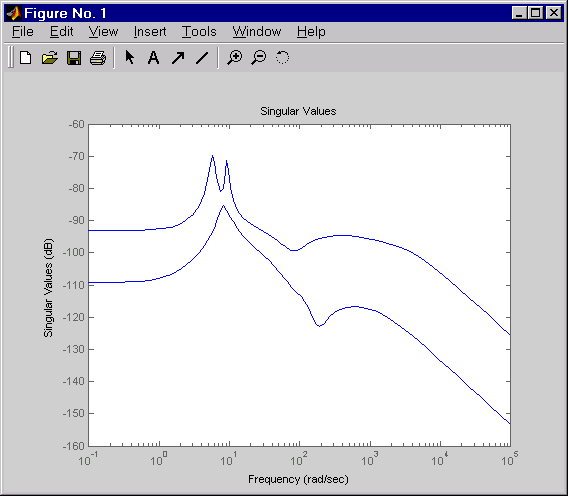
Next, plot the open- and closed-loop time responses to the white noise inputs (using the MIMO LQG regulator for feedback).
% Form the closed-loop model cl = feedback(Pc,RegMIMO,1:2,3:4,+1); % Simulate with lsim using same noise inputs lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)
Right-click on the plot that appears and select Show Input to turn off the display of the input.
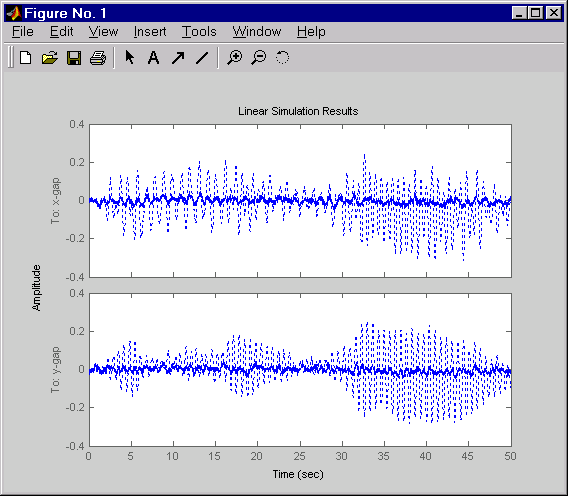
The MIMO design is a clear improvement over the separate SISO designs for each axis. In particular, the level of x/y thickness variation is now comparable to that obtained in the decoupled case. This example illustrates the benefits of direct MIMO design for multivariable systems.
References
[1] Grimble, M.J., Robust Industrial Control: Optimal Design Approach for Polynomial Systems, Prentice Hall, 1994, p. 261 and pp. 443-456.