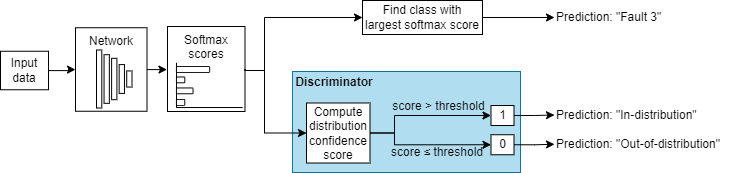
networkDistributionDiscriminator
Syntax
Description
discriminator = networkDistributionDiscriminator(net,XID,XOOD,method)method.
You can use the discriminator to classify observations as in-distribution (ID) and out-of-distribution (OOD). OOD data refers to data that is sufficiently different from the data you use to train the network, which can cause the network to behave unexpectedly. For more information, see In-Distribution and Out-of-Distribution Data.
The networkDistributionDiscriminator function first finds
distribution confidence scores using the method you specify in method. The
function then finds a threshold that best separates the ID and OOD distribution confidence
scores. You can classify any observation with a score below the threshold as OOD. For more
information about how the function computes the threshold, see Algorithms. You can find the
threshold using a set of ID data, a set of OOD data, or both.
To determine whether new data is ID or OOD, pass discriminator as
an input to the isInNetworkDistribution function.
To find the distribution confidence scores, pass discriminator as
an input to the distributionScores function. For more information about distribution
confidence scores, see Distribution Confidence Scores.
discriminator = networkDistributionDiscriminator(net,XID,[],method)Threshold property of discriminator contains the
threshold such that the discriminator attains a true positive rate greater than the value of
the TruePositiveGoal
name-value argument. For more information, see Algorithms.
discriminator = networkDistributionDiscriminator(net,[],XOOD,method)Threshold property of discriminator contains the
threshold such that the discriminator attains a false positive rate less than the value of
the FalsePositiveGoal
name-value argument. For more information, see Algorithms.
discriminator = networkDistributionDiscriminator(___,Name=Value)
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Algorithms
The function creates a discriminator using the trained network. The discriminator behaves as an additional output of the network and classifies an observation as ID or OOD using a threshold. For more information, see OOD Data Detection.
To compute the distribution threshold, the function first computes the distribution
confidence scores using the method that you specify in the method input
argument. For more information, see Distribution Confidence Scores. The software then finds the
threshold that best separates the scores of the ID and OOD data. To find the threshold, the
software optimizes over these values:
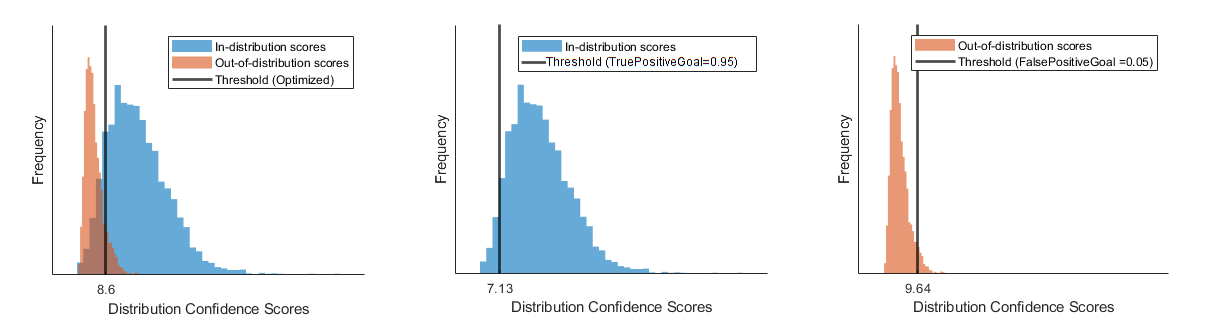
True positive goal — Number of ID observations that the discriminator correctly classifies as ID. To optimize for this value, the ID data
XIDmust be nonempty and you must specifyTruePositiveGoal. If you specifyTruePositiveGoalasp, then the software finds the threshold above which the proportion of ID confidence scores isp. This process is equivalent to finding the 100(1-p)-th percentile for the ID confidence scores.False positive goal — Number of OOD observations that the discriminator incorrectly classifies as ID. To optimize for this value, the OOD data
XOODmust be nonempty and you must specifyFalsePositiveGoal. If you specifyFalsePositiveGoalasp, then the software finds the threshold above which the proportion of OOD confidence scores isp. This process is equivalent to finding the 100p-th percentile for the OOD confidence scores.
If you provide ID and OOD data and do not specify TruePositiveGoal or
FalsePositiveGoal,
then the software finds the threshold that maximizes the balanced accuracy . If you provide only ID data, then the software optimizes using only
TruePositiveGoal,
whose default is 0.95. If you provide only OOD data, then the software
optimizes using only FalsePositiveGoal,
whose default is 0.05.
This figure illustrates the different thresholds that the software chooses if you optimize over both the true positive rate and false positive rate, just the true positive rate, or just the false positive rate.
References
[5] Jingkang Yang, Kaiyang Zhou, Yixuan Li, and Ziwei Liu, “Generalized Out-of-Distribution Detection: A Survey” August 3, 2022, http://arxiv.org/abs/2110.11334.
[6] Lee, Kimin, Kibok Lee, Honglak Lee, and Jinwoo Shin. “A Simple Unified Framework for Detecting Out-of-Distribution Samples and Adversarial Attacks.” arXiv, October 27, 2018. http://arxiv.org/abs/1807.03888.
Extended Capabilities
Version History
Introduced in R2023aSee Also
isInNetworkDistribution | distributionScores | minibatchqueue | coder.loadNetworkDistributionDiscriminator
Topics
- Verification of Neural Networks
- Out-of-Distribution Detection for Deep Neural Networks
- Out-of-Distribution Data Discriminator for YOLO v4 Object Detector
- Out-of-Distribution Detection for LSTM Document Classifier
- Out-of-Distribution Detection for BERT Document Classifier
- Verify Robustness of Deep Learning Neural Network