Neural Net Time Series
Résoudre des problèmes de séries temporelles non linéaires avec des réseaux de neurones dynamiques
Description
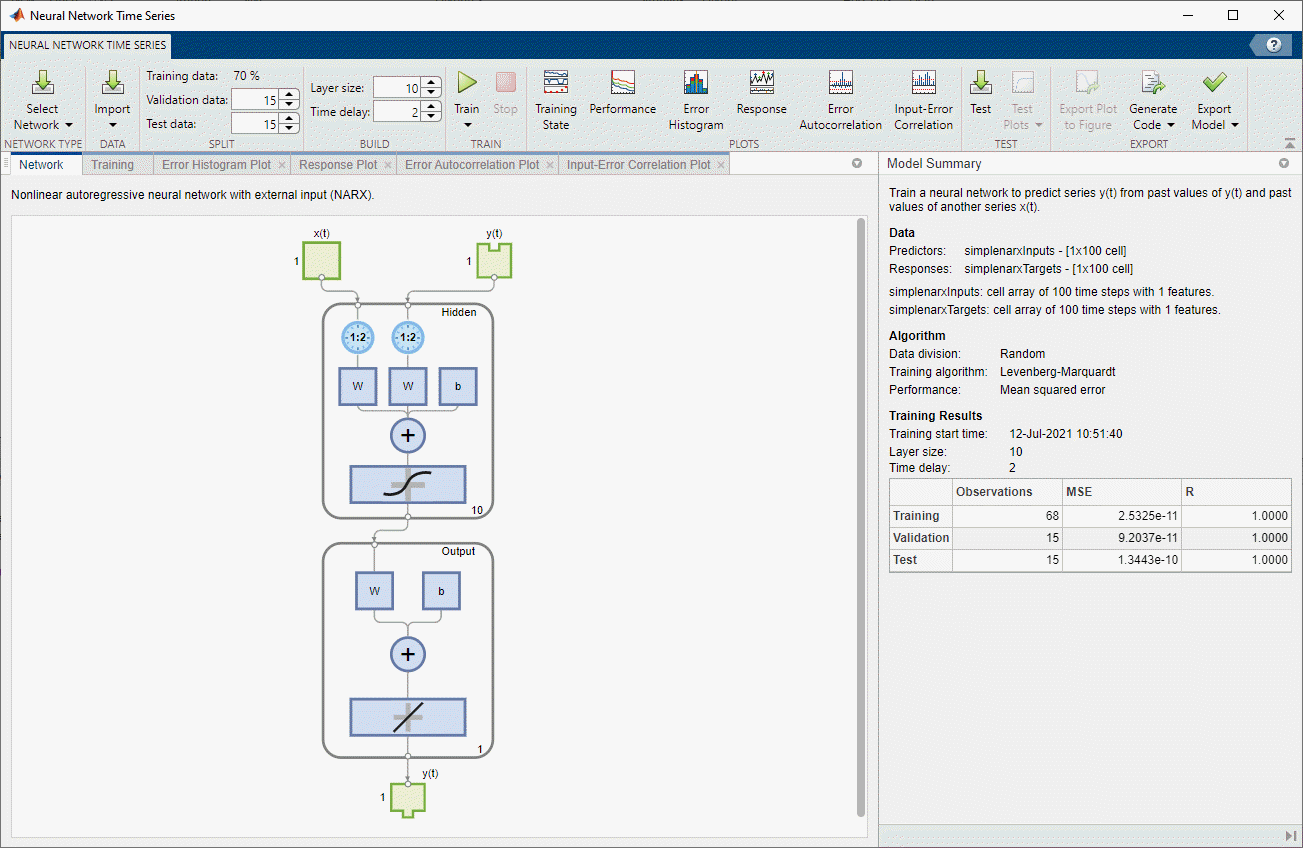
L’application Neural Net Time Series vous permet de créer, de visualiser et d’entraîner des réseaux de neurones dynamiques pour résoudre trois types de problèmes de séries temporelles non linéaires.
Avec cette application, vous pouvez :
Créer trois types de réseaux de neurones : réseau NARX, réseau NAR et réseau d’entrée-sortie non linéaire.
Importer des données depuis un fichier, l’espace de travail MATLAB® ou utiliser un des exemples de jeux de données.
Répartir les données entre les jeux d’apprentissage, de validation et de test.
Définir et entraîner un réseau de neurones.
Évaluer la performance du réseau avec une erreur quadratique moyenne et une analyse de régression.
Analyser les résultats avec des tracés de visualisation comme un tracé d’autocorrélation ou un histogramme d’erreurs.
Générer des scripts MATLAB pour reproduire des résultats et personnaliser le processus d’apprentissage.
Générer des fonctions adaptées à un déploiement avec des outils MATLAB Compiler™ et MATLAB Coder™ et les exporter vers Simulink® pour une utilisation avec Simulink Coder.
Conseil
Utilisez l’application Deep Network Designer pour créer et visualiser des réseaux de neurones de Deep Learning de manière interactive. Pour plus d’informations, veuillez consulter Démarrer avec Deep Network Designer.
Ouvrir l'application Neural Net Time Series
Barre d’outils MATLAB : dans l’onglet Apps, dans la section Machine Learning and Deep Learning, cliquez sur l’icône de l’application.
Invite de commande MATLAB : saisissez
ntstool.
Algorithmes
L’application Neural Net Time Series propose des algorithmes d’apprentissage prédéfinis que vous pouvez utiliser pour entraîner votre réseau de neurones.
| Algorithme d’apprentissage | Description |
|---|---|
| Levenberg-Marquardt | Mettre à jour les valeurs de poids et de biais selon l’optimisation de Levenberg-Marquardt. L’apprentissage de Levenberg-Marquardt est souvent l’algorithme d’apprentissage le plus rapide, bien qu’il nécessite davantage de mémoire que d’autres techniques. Pour implémenter cet algorithme, l’application Neural Net Time Series utilise la fonction |
| Régularisation bayésienne | La régularisation bayésienne met à jour les valeurs de poids et de biais selon l’optimisation de Levenberg-Marquardt. Elle minimise ensuite une combinaison d’erreurs quadratiques et de poids et détermine la combinaison correcte afin de produire un réseau avec une bonne généralisation. Cet algorithme prend généralement plus de temps mais généralise bien les jeux de données bruités ou de petite taille. Pour implémenter cet algorithme, l’application Neural Net Time Series utilise la fonction |
Rétropropagation du gradient conjugué à l’échelle | La rétropropagation du gradient conjugué à l’échelle met à jour les valeurs des poids et des biais selon la méthode du gradient conjugué à l’échelle. Pour des problèmes de grande dimension, le gradient conjugué à l’échelle est recommandé, car il utilise des calculs de gradient qui consomment moins de mémoire que les calculs jacobiens utilisés par la régularisation de Levenberg-Marquardt ou bayésienne. Pour implémenter cet algorithme, l’application Neural Net Time Series utilise la fonction |