Entraîner et appliquer des réseaux de neurones peu profonds multicouches

Conseil

Pour entraîner un réseau de Deep Learning, utilisez trainnet.

Ce sujet présente une partie du workflow d'un réseau peu profond multicouche typique. Pour plus d’informations et pour connaître les autres étapes du processus, veuillez consulter Réseaux de neurones peu profonds multicouches et apprentissage par rétropropagation.

Lorsque les poids et biais du réseau sont initialisés, le réseau est prêt pour l’apprentissage. Le réseau feedforward multicouche peut être entraîné pour l'approximation de fonctions (régression non linéaire) ou la reconnaissance de formes. Le processus d‘apprentissage nécessite un ensemble d'exemples de comportement correct du réseau : entrées du réseau p et sorties cibles t.

Le processus d‘apprentissage d'un réseau de neurones consiste à régler les valeurs des poids et biais du réseau afin d'optimiser la performance du réseau, telle que définit par la fonction de performance du réseau net.performFcn. La fonction de performance par défaut pour les réseaux feedforward est l'erreur quadratique moyenne mse, autrement dit, l'erreur quadratique moyenne entre les sorties du réseau a et les sorties cibles t. Elle est définie comme suit :

$F = m s e = \frac{1}{N} \sum_{i = 1}^{N} {(e_{i})}^{2} = \frac{1}{N} \sum_{i = 1}^{N} {(t_{i} - a_{i})}^{2}$

(Les erreurs quadratiques individuelles peuvent également être pondérées. Veuillez consulter Train Neural Networks with Error Weights.) L‘apprentissage peut être implémenté de deux manières : en mode incrémental et en mode batch. En mode incrémental, le gradient est calculé et les poids sont mis à jour après chaque entrée appliquée au réseau. En mode batch, toutes les entrées du jeu d‘apprentissage sont appliquées au réseau avant la mise à jour des poids. Ce sujet décrit l’apprentissage en mode batch avec la commande train. L’apprentissage incrémental avec la commande adapt est abordé dans Incremental Training with adapt. Pour la plupart des problèmes, lors de l’utilisation du logiciel Deep Learning Toolbox™, l‘apprentissage par batch est nettement plus rapide et donne lieu à moins d'erreurs que l‘apprentissage incrémental.

Pour l‘apprentissage des réseaux feedforward multicouches, tout algorithme d'optimisation numérique standard peut être utilisé pour optimiser la fonction de performance, mais quelques algorithmes clés ont démontré d'excellentes performances pour l'apprentissage des réseaux de neurones. Ces méthodes d'optimisation utilisent soit le gradient de performance du réseau par rapport aux poids du réseau, soit le jacobien des erreurs du réseau par rapport aux poids.

Le gradient et le jacobien sont calculés au moyen d'une technique appelée algorithme de backpropagation, qui consiste à réaliser des calculs en reculant à travers le réseau. Le calcul de la rétropropagation est dérivé de la règle de la chaîne du calcul différentiel et intégral, et est décrit aux chapitres 11 (pour le gradient) et 12 (pour le jacobien) de [HDB96].

Algorithmes d’apprentissage

Pour illustrer le fonctionnement de l’apprentissage, prenons l'exemple de l'algorithme d'optimisation le plus simple : la descente de gradient. Il met à jour les poids et biais du réseau dans la direction dans laquelle la fonction de performance diminue le plus rapidement, autrement dit dans la direction négative du gradient. Voici un exemple d’itération de cet algorithme :

$x_{k + 1} = x_{k} - α_{k} g_{k}$

où x_k est un vecteur des poids et biais actuels, g_k, le gradient actuel et α_k, le taux d’apprentissage. Cette équation est itérée jusqu’à ce que le réseau convergence.

La liste des algorithmes d‘apprentissage disponibles dans le logiciel Deep Learning Toolbox et qui utilisent des méthodes reposant sur le gradient ou le jacobien est présentée dans le tableau suivant.

Pour obtenir une description détaillée de plusieurs de ces techniques, voir aussi Hagan, M.T., H.B. Demuth, and M.H. Beale, Neural Network Design, Boston, MA : PWS Publishing, 1996, chapitres 11 et 12.

Fonction	Algorithme
`trainlm`	Levenberg-Marquardt
`trainbr`	Régularisation bayésienne
`trainbfg`	BFGS quasi-Newton
`trainrp`	Rétropropagation résiliente
`trainscg`	Gradient conjugué à l’échelle
`traincgb`	Gradient conjugué avec redémarrages Powell-Beale
`traincgf`	Gradient conjugué Fletcher-Powell
`traincgp`	Gradient conjugué Polak-Ribière
`trainoss`	Sécante en une seule étape
`traingdx`	Descente de gradient avec taux d’apprentissage variable
`traingdm`	Descente de gradient avec momentum
`traingd`	Descente de gradient

En règle générale, la fonction d‘apprentissage la plus rapide est trainlm. Il s’agit de la fonction d’apprentissage par défaut pour feedforwardnet. La méthode quasi-Newton, trainbfg, est elle aussi relativement rapide. Ces deux méthodes tendent à être moins efficaces pour les grands réseaux (avec des milliers de poids). En effet, elles nécessitent davantage de mémoire et de temps de calcul dans ces cas. En outre, trainlm permet d’obtenir de meilleurs résultats pour les problèmes d'ajustement de fonctions (régression non linéaire) que pour les problèmes de reconnaissance de formes.

Lors de l‘apprentissage de grands réseaux et de réseaux de reconnaissance de formes, il est judicieux de choisir trainscg et trainrp. Leurs exigences en matière de mémoire sont relativement faibles. Pour autant, ces algorithmes sont beaucoup plus rapides que les algorithmes standard de descente de gradient.

Voir Choose a Multilayer Neural Network Training Function pour consulter une comparaison complète de la performance des algorithmes d’apprentissage répertoriés dans le tableau ci-dessus.

En ce qui concerne la terminologie, le terme de « rétropropagation » est parfois utilisé pour faire référence spécifiquement à l'algorithme de descente de gradient lorsqu'il est appliqué à l’apprentissage des réseaux de neurones. Cette terminologie n'est pas utilisée ici étant donné que le processus de calcul du gradient et du jacobien, par le biais de calculs qui reculent à travers le réseau, est appliqué dans toutes les fonctions d'apprentissage répertoriées ci-dessus. Pour plus de clarté, il vaut mieux faire référence au nom de l'algorithme d'optimisation utilisé plutôt que de recourir au seul terme de rétropropagation.

Le réseau multicouche est lui aussi parfois appelé réseau de rétropropagation. Toutefois, la technique de rétropropagation utilisée pour calculer les gradients et jacobiens dans un réseau multicouche peut également être appliquée à de nombreuses architectures de réseau différentes. En fait, les gradients et jacobiens d'un réseau, qui a des fonctions de transfert, des fonctions de poids et des fonctions d'entrée nette différentiables, peuvent être calculés avec le logiciel Deep Learning Toolbox via un processus de rétropropagation. Vous pouvez même créer vos propres réseaux personnalisés et les entraîner en utilisant l'une des fonctions d'apprentissage présentées dans le tableau ci-dessus. Les gradients et jacobiens sont calculés automatiquement.

Exemple d’apprentissage

Pour illustrer le processus d’apprentissage, exécutez les commandes suivantes :

load bodyfat_dataset
net = feedforwardnet(20);
[net,tr] = train(net,bodyfatInputs,bodyfatTargets);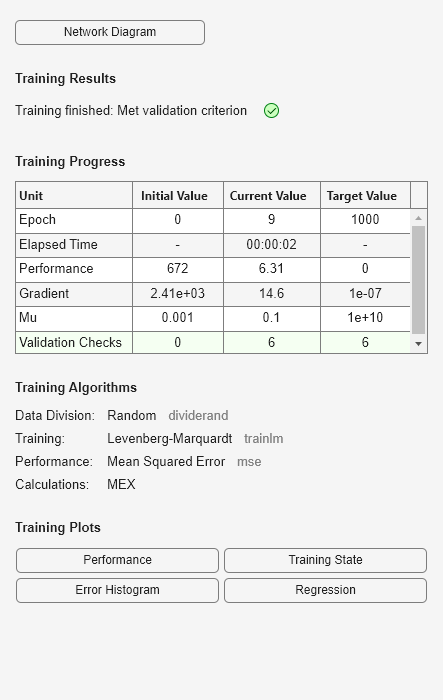

Figure Neural Network Training (09-Aug-2025 13:37:39) contains an object of type uigridlayout.

Remarque : vous n’avez pas eu besoin d’utiliser la commande configure car la fonction train effectue automatiquement la configuration. La fenêtre d’apprentissage apparaît pendant l’apprentissage, comme l’illustre la figure suivante. (Si vous ne souhaitez pas que cette fenêtre apparaisse pendant l’apprentissage, vous pouvez définir le paramètre net.trainParam.showWindow sur false. Si vous souhaitez que des informations d'apprentissage apparaissent en ligne de commande, vous pouvez définir le paramètre net.trainParam.showCommandLine sur true.)

Cette fenêtre indique que les données ont été partitionnées au moyen de la fonction dividerand et que la méthode d'apprentissage de Levenberg-Marquardt (trainlm) a été utilisée avec la fonction de performance de l'erreur quadratique moyenne. Rappelons qu'il s'agit là des paramètres par défaut pour feedforwardnet.

Pendant l’apprentissage, la progression est mise à jour constamment dans la fenêtre d’apprentissage. Les éléments essentiels sont la performance, l'amplitude du gradient de performance et le nombre de contrôles de validation. L'amplitude du gradient de performance et le nombre de contrôles de validation sont utilisés pour mettre fin à l'apprentissage. Le gradient devient très petit lorsque l‘apprentissage atteint un minimum de performance. Si l’amplitude du gradient est inférieure à 1e-5, l’apprentissage prend fin. Il est possible d’ajuster cette limite en définissant le paramètre net.trainParam.min_grad. Le nombre de contrôles de validation correspond au nombre d’itérations successives au cours desquelles la performance de validation ne réussit pas à diminuer. Si ce nombre atteint 6 (la valeur par défaut), l’apprentissage prend fin. Lors de ce cycle, vous pouvez constater que l’apprentissage a cessé en raison du nombre des contrôles de validation. Vous pouvez modifier ce critère en définissant le paramètre net.trainParam.max_fail. (Remarque : vos résultats peuvent être différents de ceux présentés dans la figure d'apprentissage du fait de la configuration aléatoire des poids et biais initiaux).

D’autres critères peuvent permettre de faire cesser l'apprentissage du réseau. Ils sont répertoriés dans le tableau suivant.

Paramètre	Critères d'arrêt
`min_grad`	Amplitude de gradient minimale
`max_fail`	Nombre maximal d’augmentations de validation
`time`	Temps d’apprentissage maximal
`goal`	Valeur de performance maximale
`epochs`	Nombre maximal d’epochs d’apprentissage (itérations)

L’apprentissage cesse également si vous cliquez sur le bouton « Stop » dans la fenêtre d’apprentissage. Vous pouvez souhaiter cet arrêt si la fonction de performance ne diminue pas de manière significative après de nombreuses itérations. Dans tous les cas, il est possible de reprendre l’apprentissage en utilisant la commande train que nous vous avons présentée précédemment. L'apprentissage du réseau reprend alors à l’endroit où il s’était arrêté lors du cycle précédent.

La fenêtre d’apprentissage vous permet d’accéder à quatre tracés : la performance, l'état de l’apprentissage, l'histogramme des erreurs et la régression. Le tracé des performance présente la valeur de la fonction de performance par rapport au nombre d’itérations. Il représente la performance d’apprentissage, de validation et de test. Le tracé de l'état de l‘apprentissage présente la progression d'autres variables de l’apprentissage, telles que l'amplitude du gradient, le nombre de contrôles de validation, etc. Le tracé de l’histogramme des erreurs présente la distribution des erreurs du réseau. Le tracé de la régression présente une régression entre les sorties et les cibles du réseau. Les tracés de l’histogramme et de la régression peuvent vous permettre de valider la performance du réseau, comme nous l'avons vu dans Analyze Shallow Neural Network Performance After Training.

Utiliser le réseau

Une fois le réseau entraîné et validé, l'objet réseau peut servir à calculer la réponse du réseau à une entrée. Par exemple, si vous souhaitez identifier la réponse du réseau au cinquième vecteur d'entrée du jeu de données de constitution, vous pouvez utiliser la commande suivante :

a = net(bodyfatInputs(:,5))

a =

   27.3740

Si vous essayez cette commande, votre résultat peut varier en fonction de l'état de votre générateur de nombres aléatoires au moment de l'initialisation du réseau. Dans ce qui suit, l'objet réseau est appelé pour calculer les sorties d’un jeu concurrent regroupant tous les vecteurs d'entrée du jeu de données de graisse corporelle. Il s'agit de la forme de simulation en mode batch, dans laquelle tous les vecteurs d'entrée sont placés dans une matrice. Cette méthode est beaucoup plus efficace que la présentation des vecteurs l’un après l’autre.

a = net(bodyfatInputs);

Chaque fois qu'un réseau de neurones est entraîné, il peut produire une solution différente en raison des valeurs initiales différentes de poids et de biais, et des différences de partition des données en jeux de données d’apprentissage, de validation et de test. Par conséquent, différents réseaux de neurones entraînés sur le même problème peuvent produire différentes sorties pour la même entrée. Pour s'assurer qu'un réseau de neurones est suffisamment précis, réalisez plusieurs apprentissages.

Il existe plusieurs autres techniques pour améliorer les résultats si vous voulez plus de précision. Pour plus d’informations, veuillez consulter Improve Shallow Neural Network Generalization and Avoid Overfitting.