GlobalSearch
Trouver le minimum global
Description
Un objet GlobalSearch contient des propriétés (options) qui affectent la manière dont run exécute à plusieurs reprises un solveur local pour générer un objet GlobalOptimSolution. Lorsqu'il est exécuté, le solveur tente de localiser une solution qui a la valeur de fonction objectif la plus basse.
Création
Syntaxe
Description
gs = GlobalSearch crée gs, un solveur GlobalSearch avec ses propriétés définies par défaut.
gs = GlobalSearch(Name,Value) définit les propriétés à l'aide de paires nom-valeur.
gs = GlobalSearch(oldGS,Name,Value) crée une copie du solveur oldGS GlobalSearch et définit les propriétés à l'aide de paires nom-valeur.
gs = GlobalSearch(ms) crée gs, un solveur GlobalSearch, avec des valeurs de propriétés communes du solveur ms MultiStart.
Propriétés
Fonctions d'objet
run | Run multiple-start solver |
Exemples
Créez un problème d’optimisation comportant plusieurs minima locaux et essayez de trouver le minimum global à l’aide de GlobalSearch. L'objectif est le problème du dos de chameau à six bosses (voir Run the Solver).
rng default % For reproducibility gs = GlobalSearch; sixmin = @(x)(4*x(1)^2 - 2.1*x(1)^4 + x(1)^6/3 ... + x(1)*x(2) - 4*x(2)^2 + 4*x(2)^4); problem = createOptimProblem('fmincon','x0',[-1,2],... 'objective',sixmin,'lb',[-3,-3],'ub',[3,3]); x = run(gs,problem)
GlobalSearch stopped because it analyzed all the trial points. All 8 local solver runs converged with a positive local solver exit flag.
x = 1×2
-0.0898 0.7127
Vous pouvez demander la valeur de la fonction objectif à x lorsque vous appelez run en utilisant la syntaxe suivante :
[x,fval] = run(gs,problem)
Cependant, si vous avez oublié de demander fval, vous pouvez toujours calculer la valeur de la fonction objectif à x.
fval = sixmin(x)
fval = -1.0316
Considérons une fonction avec plusieurs minima locaux.
fun = @(x) x.^2 + 4*sin(5*x); fplot(fun,[-5,5])
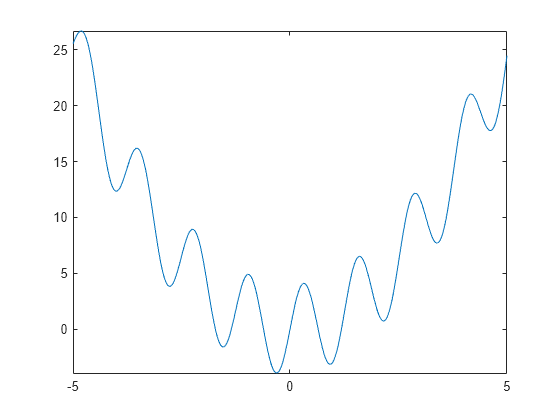
Pour rechercher le minimum global, exécutez GlobalSearch en utilisant l'algorithme fmincon 'sqp'.
rng default % For reproducibility opts = optimoptions(@fmincon,'Algorithm','sqp'); problem = createOptimProblem('fmincon','objective',... fun,'x0',3,'lb',-5,'ub',5,'options',opts); gs = GlobalSearch; [x,f] = run(gs,problem)
GlobalSearch stopped because it analyzed all the trial points. All 23 local solver runs converged with a positive local solver exit flag.
x = -0.3080
f = -3.9032
Créez un objet MultiStart sans utiliser les valeurs de tolérance par défaut.
ms = MultiStart('FunctionTolerance',2e-4,'UseParallel',true)
ms =
MultiStart with properties:
UseParallel: 1
Display: 'final'
FunctionTolerance: 2.0000e-04
MaxTime: Inf
OutputFcn: []
PlotFcn: []
StartPointsToRun: 'all'
XTolerance: 1.0000e-06
Créez un objet GlobalSearch qui utilise les propriétés disponibles à partir de ms.
gs = GlobalSearch(ms)
gs =
GlobalSearch with properties:
NumTrialPoints: 1000
BasinRadiusFactor: 0.2000
DistanceThresholdFactor: 0.7500
MaxWaitCycle: 20
NumStageOnePoints: 200
PenaltyThresholdFactor: 0.2000
Display: 'final'
FunctionTolerance: 2.0000e-04
MaxTime: Inf
OutputFcn: []
PlotFcn: []
StartPointsToRun: 'all'
XTolerance: 1.0000e-06
gs a la même valeur personnalisée (pas celle par défaut) de FunctionTolerance que ms. Mais gs n'utilise pas la propriété UseParallel.
Créez un objet GlobalSearch avec une FunctionTolerance de 1e-4.
gs = GlobalSearch('FunctionTolerance',1e-4)gs =
GlobalSearch with properties:
NumTrialPoints: 1000
BasinRadiusFactor: 0.2000
DistanceThresholdFactor: 0.7500
MaxWaitCycle: 20
NumStageOnePoints: 200
PenaltyThresholdFactor: 0.2000
Display: 'final'
FunctionTolerance: 1.0000e-04
MaxTime: Inf
OutputFcn: []
PlotFcn: []
StartPointsToRun: 'all'
XTolerance: 1.0000e-06
Mettez à jour la propriété XTolerance en 1e-3 et la propriété StartPointsToRun en 'bounds'.
gs = GlobalSearch(gs,'XTolerance',1e-3,'StartPointsToRun','bounds')
gs =
GlobalSearch with properties:
NumTrialPoints: 1000
BasinRadiusFactor: 0.2000
DistanceThresholdFactor: 0.7500
MaxWaitCycle: 20
NumStageOnePoints: 200
PenaltyThresholdFactor: 0.2000
Display: 'final'
FunctionTolerance: 1.0000e-04
MaxTime: Inf
OutputFcn: []
PlotFcn: []
StartPointsToRun: 'bounds'
XTolerance: 1.0000e-03
Vous pouvez également mettre à jour les propriétés une par une en utilisant la notation par points.
gs.MaxTime = 1800
gs =
GlobalSearch with properties:
NumTrialPoints: 1000
BasinRadiusFactor: 0.2000
DistanceThresholdFactor: 0.7500
MaxWaitCycle: 20
NumStageOnePoints: 200
PenaltyThresholdFactor: 0.2000
Display: 'final'
FunctionTolerance: 1.0000e-04
MaxTime: 1800
OutputFcn: []
PlotFcn: []
StartPointsToRun: 'bounds'
XTolerance: 1.0000e-03
Algorithmes
Pour une description détaillée de l'algorithme, voir GlobalSearch Algorithm. Ugray et al. [1] décrivent à la fois l'algorithme et la méthode de recherche par dispersion pour générer des points d'essai.
Références
[1] Ugray, Zsolt, Leon Lasdon, John Plummer, Fred Glover, James Kelly, and Rafael Martí. Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization. INFORMS Journal on Computing, Vol. 19, No. 3, 2007, pp. 328–340.
