Front de Pareto pour l'optimisation multi-objectifs, basée sur les problèmes
Cet exemple montre comment résoudre un problème d'optimisation multiobjectif à l'aide de variables d'optimisation et comment tracer la solution.
Formulation du problème
Le problème comporte une variable d’optimisation bidimensionnelle et deux fonctions objectif. Créez la variable d'optimisation x comme vecteur de ligne, l'orientation attendue par les solveurs multiobjectifs. Définissez des limites spécifiant que les composants de x varient de –50 à 50.
x = optimvar("x",1,2,LowerBound=-50,UpperBound=50);Créez la fonction objectif à deux composants. Inclure la fonction objectif dans un problème d’optimisation.
fun(1) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 - 9*x(1)^2;
fun(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 + 3*x(2)^3;
prob = optimproblem("Objective",fun);Revoyez le problème.
show(prob)
OptimizationProblem :
Solve for:
x
minimize :
((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) - (9 .* x(1).^2))
((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) + (3 .* x(2).^3))
variable bounds:
-50 <= x(1) <= 50
-50 <= x(2) <= 50
Résoudre et tracer la solution
Appelez solve pour résoudre le problème.
rng default % For reproducibility sol = solve(prob)
Solving problem using gamultiobj. gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
sol =
1x18 OptimizationValues vector with properties:
Variables properties:
x: [2x18 double]
Objective properties:
Objective: [2x18 double]
Tracez le front de Pareto résultant.
paretoplot(sol)
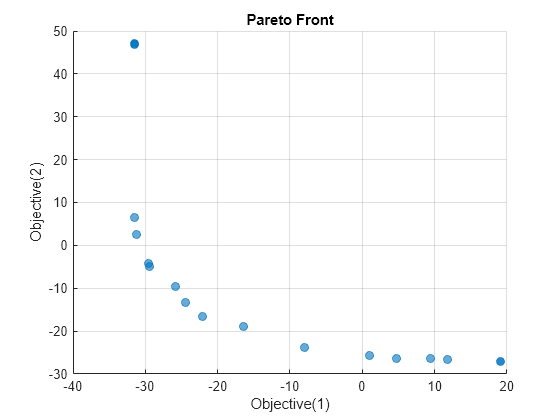
Résolvez à nouveau le problème en utilisant le solveur paretosearch.
sol2 = solve(prob,Solver="paretosearch");Solving problem using paretosearch. Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
paretoplot(sol2)
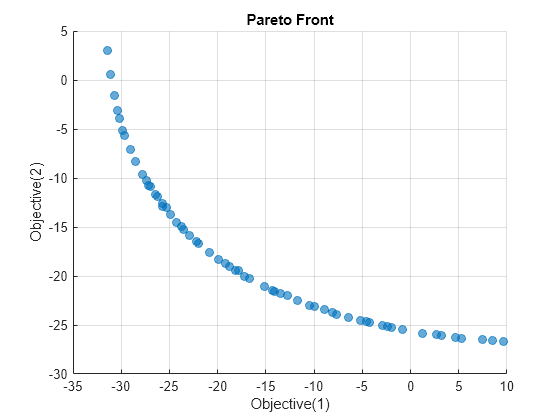
En utilisant les options par défaut, le solveur paretosearch obtient un ensemble de points de solution plus dense que gamultiobj. Cependant, gamultiobj obtient une plage de valeurs plus large.
Commencez par des solutions à objectif unique
Pour tenter d'obtenir une meilleure répartition des solutions, recherchez les solutions à objectif unique à partir de x = [1 1].
x0.x = [1 1];
prob1 = optimproblem("Objective",fun(1));
solp1 = solve(prob1,x0);Solving problem using fmincon. Local minimum possible. Constraints satisfied. fmincon stopped because the size of the current step is less than the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
prob2 = optimproblem("Objective",fun(2));
solp2 = solve(prob2,x0);Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
Préparez les solutions à objectif unique comme point de départ pour solve. Chaque point doit être transmis sous forme de vecteur colonne à la fonction optimvalues.
start = optimvalues(prob,"x",[solp1.x' solp2.x']);Résolvez le problème multiobjectif avec paretosearch à partir des points start.
sol3 = solve(prob,start,Solver="paretosearch");Solving problem using paretosearch. Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
paretoplot(sol3)
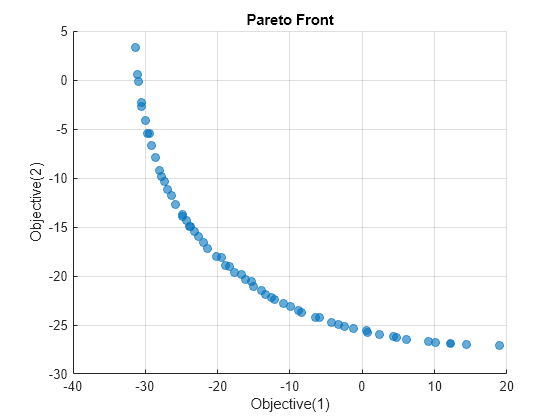
Cette fois, paretosearch trouve une gamme plus large de fonctions objectif, allant presque jusqu'à 10 dans l'Objectif 2 et presque jusqu'à 20 dans l'Objectif 1. Cette plage est similaire à la plage gamultiobj, à l'exception du point de solution anormal près de l'objectif 1 = –31, Objectif 2 = 48.
Voir aussi
gamultiobj | paretosearch | solve | paretoplot