solve
Solve optimization problem or equation problem
Syntax
Description
Use solve to find the solution of an optimization problem
or equation problem.
Tip
For the full workflow, see Problem-Based Optimization Workflow or Problem-Based Workflow for Solving Equations.
sol = solve(___,Name,Value)
Examples
Solve a linear programming problem defined by an optimization problem.
x = optimvar('x'); y = optimvar('y'); prob = optimproblem; prob.Objective = -x - y/3; prob.Constraints.cons1 = x + y <= 2; prob.Constraints.cons2 = x + y/4 <= 1; prob.Constraints.cons3 = x - y <= 2; prob.Constraints.cons4 = x/4 + y >= -1; prob.Constraints.cons5 = x + y >= 1; prob.Constraints.cons6 = -x + y <= 2; sol = solve(prob)
Solving problem using linprog. Optimal solution found.
sol = struct with fields:
x: 0.6667
y: 1.3333
Find a minimum of the peaks function, which is included in MATLAB®, in the region . To do so, create optimization variables x and y.
x = optimvar('x'); y = optimvar('y');
Create an optimization problem having peaks as the objective function.
prob = optimproblem("Objective",peaks(x,y));Include the constraint as an inequality in the optimization variables.
prob.Constraints = x^2 + y^2 <= 4;
Set the initial point for x to 1 and y to –1, and solve the problem.
x0.x = 1; x0.y = -1; sol = solve(prob,x0)
Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
sol = struct with fields:
x: 0.2283
y: -1.6255
Unsupported Functions Require fcn2optimexpr
If your objective or nonlinear constraint functions are not entirely composed of elementary functions, you must convert the functions to optimization expressions using fcn2optimexpr. See Convert Nonlinear Function to Optimization Expression and Supported Operations for Optimization Variables and Expressions.
To convert the present example:
convpeaks = fcn2optimexpr(@peaks,x,y); prob.Objective = convpeaks; sol2 = solve(prob,x0)
Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
sol2 = struct with fields:
x: 0.2283
y: -1.6255
Copyright 2018–2020 The MathWorks, Inc.
Compare the number of steps to solve an integer programming problem both with and without an initial feasible point. The problem has eight integer variables and four linear equality constraints, and all variables are restricted to be positive.
prob = optimproblem; x = optimvar('x',8,1,'LowerBound',0,'Type','integer');
Create four linear equality constraints and include them in the problem.
Aeq = [22 13 26 33 21 3 14 26
39 16 22 28 26 30 23 24
18 14 29 27 30 38 26 26
41 26 28 36 18 38 16 26];
beq = [ 7872
10466
11322
12058];
cons = Aeq*x == beq;
prob.Constraints.cons = cons;Create an objective function and include it in the problem.
f = [2 10 13 17 7 5 7 3]; prob.Objective = f*x;
Solve the problem without using an initial point, and examine the display to see the number of branch-and-bound nodes.
[x1,fval1,exitflag1,output1] = solve(prob);
Solving problem using intlinprog.
Running HiGHS 1.7.1: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
Matrix [3e+00, 4e+01]
Cost [2e+00, 2e+01]
Bound [0e+00, 0e+00]
RHS [8e+03, 1e+04]
Presolving model
4 rows, 8 cols, 32 nonzeros 0s
4 rows, 8 cols, 27 nonzeros 0s
Objective function is integral with scale 1
Solving MIP model with:
4 rows
8 cols (0 binary, 8 integer, 0 implied int., 0 continuous)
27 nonzeros
Nodes | B&B Tree | Objective Bounds | Dynamic Constraints | Work
Proc. InQueue | Leaves Expl. | BestBound BestSol Gap | Cuts InLp Confl. | LpIters Time
0 0 0 0.00% 0 inf inf 0 0 0 0 0.0s
0 0 0 0.00% 1554.047531 inf inf 0 0 4 4 0.0s
T 20753 210 8189 98.04% 1783.696925 1854 3.79% 30 8 9884 19222 2.7s
Solving report
Status Optimal
Primal bound 1854
Dual bound 1854
Gap 0% (tolerance: 0.01%)
Solution status feasible
1854 (objective)
0 (bound viol.)
9.63673585375e-14 (int. viol.)
0 (row viol.)
Timing 2.80 (total)
0.00 (presolve)
0.00 (postsolve)
Nodes 21163
LP iterations 19608 (total)
223 (strong br.)
76 (separation)
1018 (heuristics)
Optimal solution found.
Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.
For comparison, find the solution using an initial feasible point.
x0.x = [8 62 23 103 53 84 46 34]'; [x2,fval2,exitflag2,output2] = solve(prob,x0);
Solving problem using intlinprog.
Running HiGHS 1.7.1: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
Matrix [3e+00, 4e+01]
Cost [2e+00, 2e+01]
Bound [0e+00, 0e+00]
RHS [8e+03, 1e+04]
Assessing feasibility of MIP using primal feasibility and integrality tolerance of 1e-06
Solution has num max sum
Col infeasibilities 0 0 0
Integer infeasibilities 0 0 0
Row infeasibilities 0 0 0
Row residuals 0 0 0
Presolving model
4 rows, 8 cols, 32 nonzeros 0s
4 rows, 8 cols, 27 nonzeros 0s
MIP start solution is feasible, objective value is 3901
Objective function is integral with scale 1
Solving MIP model with:
4 rows
8 cols (0 binary, 8 integer, 0 implied int., 0 continuous)
27 nonzeros
Nodes | B&B Tree | Objective Bounds | Dynamic Constraints | Work
Proc. InQueue | Leaves Expl. | BestBound BestSol Gap | Cuts InLp Confl. | LpIters Time
0 0 0 0.00% 0 3901 100.00% 0 0 0 0 0.0s
0 0 0 0.00% 1554.047531 3901 60.16% 0 0 4 4 0.0s
T 6266 708 2644 73.61% 1662.791423 3301 49.63% 20 6 9746 10699 1.4s
T 9340 919 3970 80.72% 1692.410008 2687 37.01% 29 6 9995 16120 2.1s
T 21750 192 9514 96.83% 1791.542628 1854 3.37% 20 6 9984 40278 5.3s
Solving report
Status Optimal
Primal bound 1854
Dual bound 1854
Gap 0% (tolerance: 0.01%)
Solution status feasible
1854 (objective)
0 (bound viol.)
1.42108547152e-13 (int. viol.)
0 (row viol.)
Timing 5.38 (total)
0.00 (presolve)
0.00 (postsolve)
Nodes 22163
LP iterations 40863 (total)
538 (strong br.)
64 (separation)
2782 (heuristics)
Optimal solution found.
Intlinprog stopped because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.
fprintf('Without an initial point, solve took %d steps.\nWith an initial point, solve took %d steps.',output1.numnodes,output2.numnodes)Without an initial point, solve took 21163 steps. With an initial point, solve took 22163 steps.
Giving an initial point does not always improve the problem. For this problem, using an initial point saves time and computational steps. However, for some problems, an initial point can cause solve to take more steps.
For some solvers, you can pass the objective and constraint function values, if any, to solve in the x0 argument. This can save time in the solver. Pass a vector of OptimizationValues objects. Create this vector using the optimvalues function.
The solvers that can use the objective function values are:
gagamultiobjparetosearchsurrogateopt
The solvers that can use nonlinear constraint function values are:
paretosearchsurrogateopt
For example, minimize the peaks function using surrogateopt, starting with values from a grid of initial points. Create a grid from -10 to 10 in the x variable, and –5/2 to 5/2 in the y variable with spacing 1/2. Compute the objective function values at the initial points.
x = optimvar("x",LowerBound=-10,UpperBound=10); y = optimvar("y",LowerBound=-5/2,UpperBound=5/2); prob = optimproblem("Objective",peaks(x,y)); xval = -10:10; yval = (-5:5)/2; [x0x,x0y] = meshgrid(xval,yval); peaksvals = peaks(x0x,x0y);
Pass the values in the x0 argument by using optimvalues. This saves time for solve, as solve does not need to compute the values. Pass the values as row vectors.
x0 = optimvalues(prob,'x',x0x(:)','y',x0y(:)',... "Objective",peaksvals(:)');
Solve the problem using surrogateopt with the initial values.
[sol,fval,eflag,output] = solve(prob,x0,Solver="surrogateopt")Solving problem using surrogateopt.
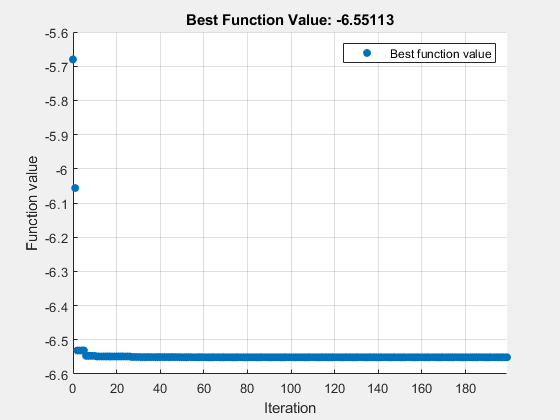
surrogateopt stopped because it exceeded the function evaluation limit set by 'options.MaxFunctionEvaluations'.
sol = struct with fields:
x: 0.2279
y: -1.6258
fval = -6.5511
eflag =
SolverLimitExceeded
output = struct with fields:
elapsedtime: 19.0362
funccount: 200
constrviolation: 0
ineq: [1×1 struct]
rngstate: [1×1 struct]
message: 'surrogateopt stopped because it exceeded the function evaluation limit set by ↵'options.MaxFunctionEvaluations'.'
solver: 'surrogateopt'
Find a local minimum of the peaks function on the range starting from the point [–1,2].
x = optimvar("x",LowerBound=-5,UpperBound=5); y = optimvar("y",LowerBound=-5,UpperBound=5); x0.x = -1; x0.y = 2; prob = optimproblem(Objective=peaks(x,y)); opts = optimoptions("fmincon",Display="none"); [sol,fval] = solve(prob,x0,Options=opts)
sol = struct with fields:
x: -3.3867
y: 3.6341
fval = 1.1224e-07
Try to find a better solution by using the GlobalSearch solver. This solver runs fmincon multiple times, which potentially yields a better solution.
ms = GlobalSearch; [sol2,fval2] = solve(prob,x0,ms)
Solving problem using GlobalSearch. GlobalSearch stopped because it analyzed all the trial points. All 15 local solver runs converged with a positive local solver exit flag.
sol2 = struct with fields:
x: 0.2283
y: -1.6255
fval2 = -6.5511
GlobalSearch finds a solution with a better (lower) objective function value. The exit message shows that fmincon, the local solver, runs 15 times. The returned solution has an objective function value of about –6.5511, which is lower than the value at the first solution, 1.1224e–07.
Solve the problem
without showing iterative display.
x = optimvar('x',2,1,'LowerBound',0); x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1); prob = optimproblem; prob.Objective = -3*x(1) - 2*x(2) - x3; prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7; prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12; options = optimoptions('intlinprog','Display','off'); sol = solve(prob,'Options',options)
sol = struct with fields:
x: [2×1 double]
x3: 0
Examine the solution.
sol.x
ans = 2×1
0
6
sol.x3
ans = 0
Force solve to use intlinprog as the solver for a linear programming problem.
x = optimvar('x'); y = optimvar('y'); prob = optimproblem; prob.Objective = -x - y/3; prob.Constraints.cons1 = x + y <= 2; prob.Constraints.cons2 = x + y/4 <= 1; prob.Constraints.cons3 = x - y <= 2; prob.Constraints.cons4 = x/4 + y >= -1; prob.Constraints.cons5 = x + y >= 1; prob.Constraints.cons6 = -x + y <= 2; sol = solve(prob,'Solver', 'intlinprog')
Solving problem using intlinprog.
Running HiGHS 1.7.1: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
Matrix [2e-01, 1e+00]
Cost [3e-01, 1e+00]
Bound [0e+00, 0e+00]
RHS [1e+00, 2e+00]
Presolving model
6 rows, 2 cols, 12 nonzeros 0s
4 rows, 2 cols, 8 nonzeros 0s
4 rows, 2 cols, 8 nonzeros 0s
Presolve : Reductions: rows 4(-2); columns 2(-0); elements 8(-4)
Solving the presolved LP
Using EKK dual simplex solver - serial
Iteration Objective Infeasibilities num(sum)
0 -1.3333333333e+03 Ph1: 3(4499); Du: 2(1.33333) 0s
3 -1.1111111111e+00 Pr: 0(0) 0s
Solving the original LP from the solution after postsolve
Model status : Optimal
Simplex iterations: 3
Objective value : -1.1111111111e+00
HiGHS run time : 0.00
Optimal solution found.
No integer variables specified. Intlinprog solved the linear problem.
sol = struct with fields:
x: 0.6667
y: 1.3333
Solve the mixed-integer linear programming problem described in Solve Integer Programming Problem with Nondefault Options and examine all of the output data.
x = optimvar('x',2,1,'LowerBound',0); x3 = optimvar('x3','Type','integer','LowerBound',0,'UpperBound',1); prob = optimproblem; prob.Objective = -3*x(1) - 2*x(2) - x3; prob.Constraints.cons1 = x(1) + x(2) + x3 <= 7; prob.Constraints.cons2 = 4*x(1) + 2*x(2) + x3 == 12; [sol,fval,exitflag,output] = solve(prob)
Solving problem using intlinprog.
Running HiGHS 1.7.1: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
Matrix [1e+00, 4e+00]
Cost [1e+00, 3e+00]
Bound [1e+00, 1e+00]
RHS [7e+00, 1e+01]
Presolving model
2 rows, 3 cols, 6 nonzeros 0s
0 rows, 0 cols, 0 nonzeros 0s
Presolve: Optimal
Solving report
Status Optimal
Primal bound -12
Dual bound -12
Gap 0% (tolerance: 0.01%)
Solution status feasible
-12 (objective)
0 (bound viol.)
0 (int. viol.)
0 (row viol.)
Timing 0.01 (total)
0.01 (presolve)
0.00 (postsolve)
Nodes 0
LP iterations 0 (total)
0 (strong br.)
0 (separation)
0 (heuristics)
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.
sol = struct with fields:
x: [2×1 double]
x3: 0
fval = -12
exitflag =
OptimalSolution
output = struct with fields:
relativegap: 0
absolutegap: 0
numfeaspoints: 1
numnodes: 0
constrviolation: 0
algorithm: 'highs'
message: 'Optimal solution found.↵↵Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.'
solver: 'intlinprog'
For a problem without any integer constraints, you can also obtain a nonempty Lagrange multiplier structure as the fifth output.
Create and solve an optimization problem using named index variables. The problem is to maximize the profit-weighted flow of fruit to various airports, subject to constraints on the weighted flows.
rng(0) % For reproducibility p = optimproblem('ObjectiveSense', 'maximize'); flow = optimvar('flow', ... {'apples', 'oranges', 'bananas', 'berries'}, {'NYC', 'BOS', 'LAX'}, ... 'LowerBound',0,'Type','integer'); p.Objective = sum(sum(rand(4,3).*flow)); p.Constraints.NYC = rand(1,4)*flow(:,'NYC') <= 10; p.Constraints.BOS = rand(1,4)*flow(:,'BOS') <= 12; p.Constraints.LAX = rand(1,4)*flow(:,'LAX') <= 35; sol = solve(p);
Solving problem using intlinprog.
Running HiGHS 1.7.1: Copyright (c) 2024 HiGHS under MIT licence terms
Coefficient ranges:
Matrix [4e-02, 1e+00]
Cost [1e-01, 1e+00]
Bound [0e+00, 0e+00]
RHS [1e+01, 4e+01]
Presolving model
3 rows, 12 cols, 12 nonzeros 0s
3 rows, 12 cols, 12 nonzeros 0s
Solving MIP model with:
3 rows
12 cols (0 binary, 12 integer, 0 implied int., 0 continuous)
12 nonzeros
Nodes | B&B Tree | Objective Bounds | Dynamic Constraints | Work
Proc. InQueue | Leaves Expl. | BestBound BestSol Gap | Cuts InLp Confl. | LpIters Time
0 0 0 0.00% 1160.150059 -inf inf 0 0 0 0 0.0s
S 0 0 0 0.00% 1160.150059 1027.233133 12.94% 0 0 0 0 0.0s
Solving report
Status Optimal
Primal bound 1027.23313332
Dual bound 1027.23313332
Gap 0% (tolerance: 0.01%)
Solution status feasible
1027.23313332 (objective)
0 (bound viol.)
0 (int. viol.)
0 (row viol.)
Timing 0.01 (total)
0.00 (presolve)
0.00 (postsolve)
Nodes 1
LP iterations 3 (total)
0 (strong br.)
0 (separation)
0 (heuristics)
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 1e-06. The intcon variables are integer within tolerance, options.ConstraintTolerance = 1e-06.
Find the optimal flow of oranges and berries to New York and Los Angeles.
[idxFruit,idxAirports] = findindex(flow, {'oranges','berries'}, {'NYC', 'LAX'})idxFruit = 1×2
2 4
idxAirports = 1×2
1 3
orangeBerries = sol.flow(idxFruit, idxAirports)
orangeBerries = 2×2
0 980
70 0
This display means that no oranges are going to NYC, 70 berries are going to NYC, 980 oranges are going to LAX, and no berries are going to LAX.
List the optimal flow of the following:
Fruit Airports
----- --------
Berries NYC
Apples BOS
Oranges LAX
idx = findindex(flow, {'berries', 'apples', 'oranges'}, {'NYC', 'BOS', 'LAX'})idx = 1×3
4 5 10
optimalFlow = sol.flow(idx)
optimalFlow = 1×3
70 28 980
This display means that 70 berries are going to NYC, 28 apples are going to BOS, and 980 oranges are going to LAX.
To solve the nonlinear system of equations
using the problem-based approach, first define x as a two-element optimization variable.
x = optimvar('x',2);Create the first equation as an optimization equality expression.
eq1 = exp(-exp(-(x(1) + x(2)))) == x(2)*(1 + x(1)^2);
Similarly, create the second equation as an optimization equality expression.
eq2 = x(1)*cos(x(2)) + x(2)*sin(x(1)) == 1/2;
Create an equation problem, and place the equations in the problem.
prob = eqnproblem; prob.Equations.eq1 = eq1; prob.Equations.eq2 = eq2;
Review the problem.
show(prob)
EquationProblem :
Solve for:
x
eq1:
exp((-exp((-(x(1) + x(2)))))) == (x(2) .* (1 + x(1).^2))
eq2:
((x(1) .* cos(x(2))) + (x(2) .* sin(x(1)))) == 0.5
Solve the problem starting from the point [0,0]. For the problem-based approach, specify the initial point as a structure, with the variable names as the fields of the structure. For this problem, there is only one variable, x.
x0.x = [0 0]; [sol,fval,exitflag] = solve(prob,x0)
Solving problem using fsolve. Equation solved. fsolve completed because the vector of function values is near zero as measured by the value of the function tolerance, and the problem appears regular as measured by the gradient. <stopping criteria details>
sol = struct with fields:
x: [2×1 double]
fval = struct with fields:
eq1: -2.4070e-07
eq2: -3.8255e-08
exitflag =
EquationSolved
View the solution point.
disp(sol.x)
0.3532
0.6061
Unsupported Functions Require fcn2optimexpr
If your equation functions are not composed of elementary functions, you must convert the functions to optimization expressions using fcn2optimexpr. For the present example:
ls1 = fcn2optimexpr(@(x)exp(-exp(-(x(1)+x(2)))),x); eq1 = ls1 == x(2)*(1 + x(1)^2); ls2 = fcn2optimexpr(@(x)x(1)*cos(x(2))+x(2)*sin(x(1)),x); eq2 = ls2 == 1/2;
See Supported Operations for Optimization Variables and Expressions and Convert Nonlinear Function to Optimization Expression.
Input Arguments
Optimization problem or equation problem, specified as an OptimizationProblem object or an EquationProblem object. Create an optimization problem by using optimproblem; create an equation problem by using eqnproblem.
Warning
The problem-based approach does not support complex values in the following: an objective function, nonlinear equalities, and nonlinear inequalities. If a function calculation has a complex value, even as an intermediate value, the final result might be incorrect.
Example: prob = optimproblem; prob.Objective = obj; prob.Constraints.cons1 =
cons1;
Example: prob = eqnproblem; prob.Equations = eqs;
Initial point, specified as a structure with field names equal to the variable names in prob.
For some Global Optimization Toolbox solvers, x0 can be a vector of OptimizationValues objects representing multiple initial points. Create
the points using the optimvalues
function. These solvers are:
ga(Global Optimization Toolbox),gamultiobj(Global Optimization Toolbox),paretosearch(Global Optimization Toolbox) andparticleswarm(Global Optimization Toolbox). These solvers accept multiple starting points as members of the initial population.MultiStart(Global Optimization Toolbox). This solver accepts multiple initial points for a local solver such asfmincon.surrogateopt(Global Optimization Toolbox). This solver accepts multiple initial points to help create an initial surrogate.
For an example using x0 with named index variables, see Create Initial Point for Optimization with Named Index Variables.
Example: If prob has variables named x and y: x0.x = [3,2,17]; x0.y = [pi/3,2*pi/3].
Data Types: struct
Multiple start solver, specified as a MultiStart (Global Optimization Toolbox) object or a GlobalSearch (Global Optimization Toolbox) object. Create
ms using the MultiStart or
GlobalSearch commands.
Currently, GlobalSearch supports only the
fmincon local solver, and
MultiStart supports only the
fmincon, fminunc, and
lsqnonlin local solvers.
Example: ms = MultiStart;
Example: ms =
GlobalSearch(FunctionTolerance=1e-4);
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: solve(prob,'Options',opts)
Minimum number of start points for MultiStart (Global Optimization Toolbox), specified as a
positive integer. This argument applies only when you call
solve using the ms
argument. solve uses all of the values in
x0 as start points. If
MinNumStartPoints is greater than the number of
values in x0, then solve
generates more start points uniformly at random within the problem
bounds. If a component is unbounded, solve
generates points using the default artificial bounds for
MultiStart.
Example: solve(prob,x0,ms,MinNumStartPoints=50)
Data Types: double
Optimization options, specified as an object created by optimoptions or an options
structure such as created by optimset.
Internally, the solve function calls a relevant
solver as detailed in the 'solver' argument reference. Ensure that
options is compatible with the solver. For
example, intlinprog does not allow options to be a
structure, and lsqnonneg does not allow options to be
an object.
For suggestions on options settings to improve an
intlinprog solution or the speed of a solution,
see Tuning Integer Linear Programming. For linprog, the
default 'dual-simplex' algorithm is generally
memory-efficient and speedy. Occasionally, linprog
solves a large problem faster when the Algorithm
option is 'interior-point'. For suggestions on
options settings to improve a nonlinear problem's solution, see Optimization Options in Common Use: Tuning and Troubleshooting and Improve Results.
Example: options =
optimoptions('intlinprog','Display','none')
Optimization solver, specified as the name of a listed solver. For optimization problems, this table contains the available solvers for each problem type, including solvers from Global Optimization Toolbox. Details for equation problems appear below the optimization solver details.
For converting nonlinear problems with integer constraints using
prob2struct, the resulting problem structure can depend on the
chosen solver. If you do not have a Global Optimization Toolbox license, you must specify the solver. See Integer Constraints in Nonlinear Problem-Based Optimization.
The default solver for each optimization problem type is listed here.
| Problem Type | Default Solver |
|---|---|
| Linear Programming (LP) | linprog |
| Mixed-Integer Linear Programming (MILP) | intlinprog |
| Quadratic Programming (QP) | quadprog |
| Second-Order Cone Programming (SOCP) | coneprog |
| Linear Least Squares | lsqlin |
| Nonlinear Least Squares | lsqnonlin |
| Nonlinear Programming (NLP) | |
| Mixed-Integer Nonlinear Programming (MINLP) | ga (Global Optimization Toolbox) |
| Multiobjective | gamultiobj (Global Optimization Toolbox) |
In this table, ![]() means the solver is available for the problem type,
x means the solver is not available.
means the solver is available for the problem type,
x means the solver is not available.
Problem Type | LP | MILP | QP | SOCP | Linear Least Squares | Nonlinear Least Squares | NLP | MINLP |
|---|---|---|---|---|---|---|---|---|
| Solver | ||||||||
linprog |
| x | x | x | x | x | x | x |
intlinprog |
|
| x | x | x | x | x | x |
quadprog |
| x |
|
|
| x | x | x |
coneprog |
| x | x |
| x | x | x | x |
lsqlin | x | x | x | x |
| x | x | x |
lsqnonneg | x | x | x | x |
| x | x | x |
lsqnonlin | x | x | x | x |
|
| x | x |
fminunc |
| x |
| x |
|
|
| x |
fmincon |
| x |
|
|
|
|
| x |
fminbnd | x | x | x | x |
|
|
| x |
fminsearch | x | x | x | x |
|
|
| x |
patternsearch (Global Optimization Toolbox) |
| x |
|
|
|
|
| x |
ga (Global Optimization Toolbox) |
|
|
|
|
|
|
|
|
particleswarm (Global Optimization Toolbox) |
| x |
| x |
|
|
| x |
simulannealbnd (Global Optimization Toolbox) |
| x |
| x |
|
|
| x |
surrogateopt (Global Optimization Toolbox) |
|
|
|
|
|
|
|
|
gamultiobj (Global Optimization Toolbox) |
|
|
|
|
|
|
|
|
paretosearch (Global Optimization Toolbox) |
| x |
|
|
|
|
| x |
Note
If you choose lsqcurvefit as the solver for a least-squares
problem, solve uses lsqnonlin. The
lsqcurvefit and lsqnonlin solvers are
identical for solve.
Caution
For maximization problems (prob.ObjectiveSense is
"max" or "maximize"), do not specify a
least-squares solver (one with a name beginning lsq). If you do,
solve throws an error, because these solvers cannot
maximize.
For equation solving, this table contains the available solvers for each problem type. In the table,
* indicates the default solver for the problem type.
Y indicates an available solver.
N indicates an unavailable solver.
Supported Solvers for Equations
| Equation Type | lsqlin | lsqnonneg | fzero | fsolve | lsqnonlin |
|---|---|---|---|---|---|
| Linear | * | N | Y (scalar only) | Y | Y |
| Linear plus bounds | * | Y | N | N | Y |
| Scalar nonlinear | N | N | * | Y | Y |
| Nonlinear system | N | N | N | * | Y |
| Nonlinear system plus bounds | N | N | N | N | * |
Example: 'intlinprog'
Data Types: char | string
Indication to use automatic differentiation (AD) for nonlinear
objective function, specified as 'auto' (use AD if
possible), 'auto-forward' (use forward AD if
possible), 'auto-reverse' (use reverse AD if
possible), or 'finite-differences' (do not use AD).
Choices including auto cause the underlying solver to
use gradient information when solving the problem provided that the
objective function is supported, as described in Supported Operations for Optimization Variables and Expressions. For
an example, see Effect of Automatic Differentiation in Problem-Based Optimization.
Solvers choose the following type of AD by default:
For a general nonlinear objective function,
fmincondefaults to reverse AD for the objective function.fmincondefaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise,fmincondefaults to forward AD for the nonlinear constraint function.For a general nonlinear objective function,
fminuncdefaults to reverse AD.For a least-squares objective function,
fminconandfminuncdefault to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.lsqnonlindefaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise,lsqnonlindefaults to reverse AD.fsolvedefaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise,fsolvedefaults to reverse AD.
Example: 'finite-differences'
Data Types: char | string
Indication to use automatic differentiation (AD) for nonlinear
constraint functions, specified as 'auto' (use AD if
possible), 'auto-forward' (use forward AD if
possible), 'auto-reverse' (use reverse AD if
possible), or 'finite-differences' (do not use AD).
Choices including auto cause the underlying solver to
use gradient information when solving the problem provided that the
constraint functions are supported, as described in Supported Operations for Optimization Variables and Expressions. For
an example, see Effect of Automatic Differentiation in Problem-Based Optimization.
Solvers choose the following type of AD by default:
For a general nonlinear objective function,
fmincondefaults to reverse AD for the objective function.fmincondefaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise,fmincondefaults to forward AD for the nonlinear constraint function.For a general nonlinear objective function,
fminuncdefaults to reverse AD.For a least-squares objective function,
fminconandfminuncdefault to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.lsqnonlindefaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise,lsqnonlindefaults to reverse AD.fsolvedefaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise,fsolvedefaults to reverse AD.
Example: 'finite-differences'
Data Types: char | string
Indication to use automatic differentiation (AD) for nonlinear
constraint functions, specified as 'auto' (use AD if
possible), 'auto-forward' (use forward AD if
possible), 'auto-reverse' (use reverse AD if
possible), or 'finite-differences' (do not use AD).
Choices including auto cause the underlying solver to
use gradient information when solving the problem provided that the
equation functions are supported, as described in Supported Operations for Optimization Variables and Expressions. For
an example, see Effect of Automatic Differentiation in Problem-Based Optimization.
Solvers choose the following type of AD by default:
For a general nonlinear objective function,
fmincondefaults to reverse AD for the objective function.fmincondefaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise,fmincondefaults to forward AD for the nonlinear constraint function.For a general nonlinear objective function,
fminuncdefaults to reverse AD.For a least-squares objective function,
fminconandfminuncdefault to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.lsqnonlindefaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise,lsqnonlindefaults to reverse AD.fsolvedefaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise,fsolvedefaults to reverse AD.
Example: 'finite-differences'
Data Types: char | string
Output Arguments
Solution, returned as a structure or an OptimizationValues vector. sol is an
OptimizationValues vector when the problem is multiobjective. For
single-objective problems, the fields of the returned structure are the names of the
optimization variables in the problem. See optimvar.
Objective function value at the solution, returned as one of the following:
| Problem Type | Returned Value(s) |
|---|---|
| Optimize scalar objective function f(x) | Real number f(sol) |
| Least squares | Real number, the sum of squares of the residuals at the solution |
| Solve equation | If prob.Equations is a single entry:
Real vector of function values at the solution, meaning the
left side minus the right side of the equations |
If prob.Equations has multiple named
fields: Structure with same names as
prob.Equations, where each field
value is the left side minus the right side of the named
equations | |
| Multiobjective | Matrix with one row for each objective function component, and one column for each solution point. |
Tip
If you neglect to ask for fval for an objective
defined as an optimization expression or equation expression, you can
calculate it using
fval = evaluate(prob.Objective,sol)
If the objective is defined as a structure with only one field,
fval = evaluate(prob.Objective.ObjectiveName,sol)
If the objective is a structure with multiple fields, write a loop.
fnames = fields(prob.Equations); for i = 1:length(fnames) fval.(fnames{i}) = evaluate(prob.Equations.(fnames{i}),sol); end
Reason the solver stopped, returned as an enumeration variable. You can convert
exitflag to its numeric equivalent using
double(exitflag), and to its string equivalent using
string(exitflag).
This table describes the exit flags for the intlinprog
solver.
Exit Flag for intlinprog | Numeric Equivalent | Meaning |
|---|---|---|
OptimalWithPoorFeasibility | 3 | The solution is feasible with respect to the relative
|
IntegerFeasible | 2 | intlinprog stopped prematurely, and found an
integer feasible point. |
OptimalSolution |
| The solver converged to a solution
|
SolverLimitExceeded |
|
See Tolerances and Stopping Criteria. |
OutputFcnStop | -1 | intlinprog stopped by an output function or plot
function. |
NoFeasiblePointFound |
| No feasible point found. |
Unbounded |
| The problem is unbounded. |
FeasibilityLost |
| Solver lost feasibility. |
Exitflags 3 and -9 relate
to solutions that have large infeasibilities. These usually arise from linear constraint
matrices that have large condition number, or problems that have large solution components. To
correct these issues, try to scale the coefficient matrices, eliminate redundant linear
constraints, or give tighter bounds on the variables.
This table describes the exit flags for the linprog solver.
Exit Flag for linprog | Numeric Equivalent | Meaning |
|---|---|---|
OptimalWithPoorFeasibility | 3 | The solution is feasible with respect to the relative
|
OptimalSolution | 1 | The solver converged to a solution
|
SolverLimitExceeded | 0 | The number of iterations exceeds
|
NoFeasiblePointFound | -2 | No feasible point found. |
Unbounded | -3 | The problem is unbounded. |
FoundNaN | -4 |
|
PrimalDualInfeasible | -5 | Both primal and dual problems are infeasible. |
DirectionTooSmall | -7 | The search direction is too small. No further progress can be made. |
FeasibilityLost | -9 | Solver lost feasibility. |
Exitflags 3 and -9 relate
to solutions that have large infeasibilities. These usually arise from linear constraint
matrices that have large condition number, or problems that have large solution components. To
correct these issues, try to scale the coefficient matrices, eliminate redundant linear
constraints, or give tighter bounds on the variables.
This table describes the exit flags for the lsqlin solver.
Exit Flag for lsqlin | Numeric Equivalent | Meaning |
|---|---|---|
FunctionChangeBelowTolerance | 3 | Change in the residual is smaller than the specified tolerance
|
StepSizeBelowTolerance |
| Step size smaller than
|
OptimalSolution | 1 | The solver converged to a solution
|
SolverLimitExceeded | 0 | The number of iterations exceeds
|
NoFeasiblePointFound | -2 | For optimization problems, the problem is infeasible. Or, for
the For equation problems, no solution found. |
IllConditioned | -4 | Ill-conditioning prevents further optimization. |
NoDescentDirectionFound | -8 | The search direction is too small. No further progress can be
made. ( |
This table describes the exit flags for the quadprog solver.
Exit Flag for quadprog | Numeric Equivalent | Meaning |
|---|---|---|
LocalMinimumFound | 4 | Local minimum found; minimum is not unique. |
FunctionChangeBelowTolerance | 3 | Change in the objective function value is smaller than the
specified tolerance |
StepSizeBelowTolerance |
| Step size smaller than
|
OptimalSolution | 1 | The solver converged to a solution
|
SolverLimitExceeded | 0 | The number of iterations exceeds
|
NoFeasiblePointFound | -2 | The problem is infeasible. Or, for the
|
IllConditioned | -4 | Ill-conditioning prevents further optimization. |
Nonconvex |
| Nonconvex problem detected.
( |
NoDescentDirectionFound | -8 | Unable to compute a step direction.
( |
This table describes the exit flags for the coneprog solver.
Exit Flag for coneprog | Numeric Equivalent | Meaning |
|---|---|---|
OptimalSolution | 1 | The solver converged to a solution
|
SolverLimitExceeded | 0 | The number of iterations exceeds
|
NoFeasiblePointFound | -2 | The problem is infeasible. |
Unbounded | -3 | The problem is unbounded. |
DirectionTooSmall |
| The search direction became too small. No further progress could be made. |
Unstable | -10 | The problem is numerically unstable. |
This table describes the exit flags for the lsqcurvefit or
lsqnonlin solver.
Exit Flag for lsqnonlin | Numeric Equivalent | Meaning |
|---|---|---|
SearchDirectionTooSmall | 4 | Magnitude of search direction was smaller than
|
FunctionChangeBelowTolerance | 3 | Change in the residual was less than
|
StepSizeBelowTolerance |
| Step size smaller than
|
OptimalSolution | 1 | The solver converged to a solution
|
SolverLimitExceeded | 0 | Number of iterations exceeded
|
OutputFcnStop | -1 | Stopped by an output function or plot function. |
NoFeasiblePointFound | -2 | For optimization problems, problem is infeasible: the bounds
For equation problems, no solution found. |
This table describes the exit flags for the fminunc solver.
Exit Flag for fminunc | Numeric Equivalent | Meaning |
|---|---|---|
NoDecreaseAlongSearchDirection | 5 | Predicted decrease in the objective function is less than the
|
FunctionChangeBelowTolerance | 3 | Change in the objective function value is less than the
|
StepSizeBelowTolerance |
| Change in |
OptimalSolution | 1 | Magnitude of gradient is smaller than the
|
SolverLimitExceeded | 0 | Number of iterations exceeds
|
OutputFcnStop | -1 | Stopped by an output function or plot function. |
Unbounded | -3 | Objective function at current iteration is below
|
This table describes the exit flags for the fmincon solver.
Exit Flag for fmincon | Numeric Equivalent | Meaning |
|---|---|---|
NoDecreaseAlongSearchDirection | 5 | Magnitude of directional derivative in search direction is less
than 2* |
SearchDirectionTooSmall | 4 | Magnitude of the search direction is less than
2* |
FunctionChangeBelowTolerance | 3 | Change in the objective function value is less than
|
StepSizeBelowTolerance |
| Change in |
OptimalSolution | 1 | First-order optimality measure is less than
|
SolverLimitExceeded | 0 | Number of iterations exceeds
|
OutputFcnStop | -1 | Stopped by an output function or plot function. |
NoFeasiblePointFound | -2 | No feasible point found. |
Unbounded | -3 | Objective function at current iteration is below
|
This table describes the exit flags for the fsolve solver.
Exit Flag for fsolve | Numeric Equivalent | Meaning |
|---|---|---|
SearchDirectionTooSmall | 4 | Magnitude of the search direction is less than
|
FunctionChangeBelowTolerance | 3 | Change in the objective function value is less than
|
StepSizeBelowTolerance |
| Change in |
OptimalSolution | 1 | First-order optimality measure is less than
|
SolverLimitExceeded | 0 | Number of iterations exceeds
|
OutputFcnStop | -1 | Stopped by an output function or plot function. |
NoFeasiblePointFound | -2 | Converged to a point that is not a root. |
TrustRegionRadiusTooSmall | -3 | Equation not solved. Trust region radius became too small
( |
This table describes the exit flags for the fzero solver.
Exit Flag for fzero | Numeric Equivalent | Meaning |
|---|---|---|
OptimalSolution | 1 | Equation solved. |
OutputFcnStop | -1 | Stopped by an output function or plot function. |
FoundNaNInfOrComplex | -4 |
|
SingularPoint | -5 | Might have converged to a singular point. |
CannotDetectSignChange | -6 | Did not find two points with opposite signs of function value. |
This table describes the exit flags for the patternsearch
solver.
Exit Flag for patternsearch | Numeric Equivalent | Meaning |
|---|---|---|
SearchDirectionTooSmall | 4 | The magnitude of the step is smaller than machine precision,
and the constraint violation is less than
|
FunctionChangeBelowTolerance | 3 | The change in |
StepSizeBelowTolerance |
| Change in |
SolverConvergedSuccessfully | 1 | Without nonlinear constraints
— The magnitude of the mesh size is less than the specified
tolerance, and the constraint violation is less than
|
With nonlinear constraints
— The magnitude of the complementarity
measure (defined after this table) is less than
| ||
SolverLimitExceeded | 0 | The maximum number of function evaluations or iterations is reached. |
OutputFcnStop | -1 | Stopped by an output function or plot function. |
NoFeasiblePointFound | -2 | No feasible point found. |
In the nonlinear constraint solver, the complementarity measure is the norm of the vector whose elements are ciλi, where ci is the nonlinear inequality constraint violation, and λi is the corresponding Lagrange multiplier.
This table describes the exit flags for the ga solver.
Exit Flag for ga | Numeric Equivalent | Meaning |
|---|---|---|
MinimumFitnessLimitReached | 5 | Minimum fitness limit |
SearchDirectionTooSmall | 4 | The magnitude of the step is smaller than machine precision,
and the constraint violation is less than
|
FunctionChangeBelowTolerance | 3 | Value of the fitness function did not change in
|
SolverConvergedSuccessfully | 1 | Without nonlinear constraints
— Average cumulative change in value of the fitness function
over |
With nonlinear constraints
— Magnitude of the complementarity measure (see Complementarity Measure (Global Optimization Toolbox)) is
less than | ||
SolverLimitExceeded | 0 | Maximum number of generations |
OutputFcnStop | -1 | Stopped by an output function or plot function. |
NoFeasiblePointFound | -2 | No feasible point found. |
StallTimeLimitExceeded | -4 | Stall time limit |
TimeLimitExceeded | -5 | Time limit |
This table describes the exit flags for the particleswarm
solver.
Exit Flag for particleswarm | Numeric Equivalent | Meaning |
|---|---|---|
SolverConvergedSuccessfully | 1 | Relative change in the objective value over the last
|
SolverLimitExceeded | 0 | Number of iterations exceeded
|
OutputFcnStop | -1 | Iterations stopped by output function or plot function. |
NoFeasiblePointFound | -2 | Bounds are inconsistent: for some |
Unbounded | -3 | Best objective function value is below
|
StallTimeLimitExceeded | -4 | Best objective function value did not change within
|
TimeLimitExceeded | -5 | Run time exceeded |
This table describes the exit flags for the simulannealbnd
solver.
Exit Flag for simulannealbnd | Numeric Equivalent | Meaning |
|---|---|---|
ObjectiveValueBelowLimit | 5 | Objective function value is less than
|
SolverConvergedSuccessfully | 1 | Average change in the value of the objective function over
|
SolverLimitExceeded | 0 | Maximum number of generations |
OutputFcnStop | -1 | Optimization terminated by an output function or plot function. |
NoFeasiblePointFound | -2 | No feasible point found. |
TimeLimitExceeded | -5 | Time limit exceeded. |
This table describes the exit flags for the surrogateopt
solver.
Exit Flag for surrogateopt | Numeric Equivalent | Meaning |
|---|---|---|
BoundsEqual | 10 | Problem has a unique feasible solution due to one of the following:
|
FeasiblePointFound | 3 | Feasible point found. Solver stopped because too few new feasible points were found to continue. |
ObjectiveLimitAttained | 1 | The objective function value is less than
|
SolverLimitExceeded | 0 | The number of function evaluations exceeds
|
OutputFcnStop | -1 | The optimization is terminated by an output function or plot function. |
NoFeasiblePointFound | -2 | No feasible point is found due to one of the following:
|
This table describes the exit flags for the MultiStart and
GlobalSearch solvers.
Exit Flag for MultiStart or
GlobalSearch | Numeric Equivalent | Meaning |
|---|---|---|
LocalMinimumFoundSomeConverged | 2 | At least one local minimum found. Some runs of the local solver converged. |
LocalMinimumFoundAllConverged | 1 | At least one local minimum found. All runs of the local solver converged. |
SolverLimitExceeded | 0 | No local minimum found. Local solver called at least once and at least one local solver call ran out of iterations. |
OutputFcnStop | –1 | Stopped by an output function or plot function. |
NoFeasibleLocalMinimumFound | –2 | No feasible local minimum found. |
TimeLimitExceeded | –5 | MaxTime limit exceeded. |
NoSolutionFound | –8 | No solution found. All runs had local solver exit flag –2 or smaller, not all equal –2. |
FailureInSuppliedFcn | –10 | Encountered failures in the objective or nonlinear constraint functions. |
This table describes the exit flags for the paretosearch
solver.
Exit Flag for paretosearch | Numeric Equivalent | Meaning |
|---|---|---|
SolverConvergedSuccessfully | 1 | One of the following conditions is met:
|
SolverLimitExceeded | 0 | Number of iterations exceeds
options.MaxIterations, or the number of function
evaluations exceeds
options.MaxFunctionEvaluations. |
OutputFcnStop | –1 | Stopped by an output function or plot function. |
NoFeasiblePointFound | –2 | Solver cannot find a point satisfying all the constraints. |
TimeLimitExceeded | –5 | Optimization time exceeds options.MaxTime. |
This table describes the exit flags for the gamultiobj
solver.
Exit Flag for paretosearch | Numeric Equivalent | Meaning |
|---|---|---|
SolverConvergedSuccessfully | 1 | Geometric average of the relative change in value of the spread over
options.MaxStallGenerations generations is less
than options.FunctionTolerance, and the final spread
is less than the mean spread over the past
options.MaxStallGenerations generations. |
SolverLimitExceeded | 0 | Number of generations exceeds
options.MaxGenerations. |
OutputFcnStop | –1 | Stopped by an output function or plot function. |
NoFeasiblePointFound | –2 | Solver cannot find a point satisfying all the constraints. |
TimeLimitExceeded | –5 | Optimization time exceeds options.MaxTime. |
Information about the optimization process, returned as a structure. The output
structure contains the fields in the relevant underlying solver output field, depending
on which solver solve called:
'ga'output(Global Optimization Toolbox)'gamultiobj'output(Global Optimization Toolbox)'paretosearch'output(Global Optimization Toolbox)'particleswarm'output(Global Optimization Toolbox)'patternsearch'output(Global Optimization Toolbox)'simulannealbnd'output(Global Optimization Toolbox)'surrogateopt'output(Global Optimization Toolbox)
'MultiStart'and'GlobalSearch'return the output structure from the local solver. In addition, the output structure contains the following fields:globalSolver— Either'MultiStart'or'GlobalSearch'.objectiveDerivative— Takes the values described at the end of this section.constraintDerivative— Takes the values described at the end of this section, or"auto"whenprobhas no nonlinear constraint.solver— The local solver, such as'fmincon'.local— Structure containing extra information about the optimization.sol— Local solutions, returned as a vector ofOptimizationValuesobjects.x0— Initial points for the local solver, returned as a cell array.exitflag— Exit flags of local solutions, returned as an integer vector.output— Structure array, with one row for each local solution. Each row is the local output structure corresponding to one local solution.
solve includes the additional field Solver in
the output structure to identify the solver used, such as
'intlinprog'.
When Solver is a nonlinear Optimization Toolbox™ solver, solve includes one or two extra fields
describing the derivative estimation type. The objectivederivative
and, if appropriate, constraintderivative fields can take the
following values:
"reverse-AD"for reverse automatic differentiation"forward-AD"for forward automatic differentiation"finite-differences"for finite difference estimation"closed-form"for linear or quadratic functions
For details, see Automatic Differentiation Background.
Lagrange multipliers at the solution, returned as a structure.
Note
solve does not return lambda for
equation-solving problems.
For the intlinprog and fminunc solvers,
lambda is empty, []. For the other solvers,
lambda has these fields:
Variables– Contains fields for each problem variable. Each problem variable name is a structure with two fields:Lower– Lagrange multipliers associated with the variableLowerBoundproperty, returned as an array of the same size as the variable. Nonzero entries mean that the solution is at the lower bound. These multipliers are in the structurelambda.Variables..variablename.LowerUpper– Lagrange multipliers associated with the variableUpperBoundproperty, returned as an array of the same size as the variable. Nonzero entries mean that the solution is at the upper bound. These multipliers are in the structurelambda.Variables..variablename.Upper
Constraints– Contains a field for each problem constraint. Each problem constraint is in a structure whose name is the constraint name, and whose value is a numeric array of the same size as the constraint. Nonzero entries mean that the constraint is active at the solution. These multipliers are in the structurelambda.Constraints..constraintnameNote
Elements of a constraint array all have the same comparison (
<=,==, or>=) and are all of the same type (linear, quadratic, or nonlinear).
Algorithms
Internally, the solve function
solves optimization problems by calling a solver. For the default solver for the problem and
supported solvers for the problem, see the solvers
function. You can override the default by using the 'solver' name-value pair argument when calling
solve.
Before solve can call a
solver, the problems must be converted to solver form, either by solve or
some other associated functions or objects. This conversion entails, for example, linear
constraints having a matrix representation rather than an optimization variable
expression.
The first step in the algorithm occurs as you place
optimization expressions into the problem. An OptimizationProblem object has an internal list of the variables used in its
expressions. Each variable has a linear index in the expression, and a size. Therefore, the
problem variables have an implied matrix form. The prob2struct
function performs the conversion from problem form to solver form. For an example, see Convert Problem to Structure.
For nonlinear optimization problems, solve uses automatic
differentiation to compute the gradients of the objective function and
nonlinear constraint functions. These derivatives apply when the objective and constraint
functions are composed of Supported Operations for Optimization Variables and Expressions. When automatic
differentiation does not apply, solvers estimate derivatives using finite differences. For
details of automatic differentiation, see Automatic Differentiation Background. You can control how
solve uses automatic differentiation with the ObjectiveDerivative name-value argument.
For the algorithm that
intlinprog uses to solve MILP problems, see Legacy intlinprog Algorithm. For
the algorithms that linprog uses to solve linear programming problems,
see Linear Programming Algorithms.
For the algorithms that quadprog uses to solve quadratic programming
problems, see Quadratic Programming Algorithms. For linear or nonlinear least-squares solver
algorithms, see Least-Squares (Model Fitting) Algorithms. For nonlinear solver algorithms, see Unconstrained Nonlinear Optimization Algorithms and
Constrained Nonlinear Optimization Algorithms.
For Global Optimization Toolbox solver algorithms, see Global Optimization Toolbox documentation.
For nonlinear equation solving, solve internally represents each
equation as the difference between the left and right sides. Then solve
attempts to minimize the sum of squares of the equation components. For the algorithms for
solving nonlinear systems of equations, see Equation Solving Algorithms. When
the problem also has bounds, solve calls lsqnonlin
to minimize the sum of squares of equation components. See Least-Squares (Model Fitting) Algorithms.
Note
If your objective function is a sum of squares, and you want solve
to recognize it as such, write it as either norm(expr)^2 or
sum(expr.^2), and not as expr'*expr or any
other form. The internal parser recognizes a sum of squares only when represented as a
square of a norm or an explicit sums of squares. For details, see Write Objective Function for Problem-Based Least Squares. For an example, see
Nonnegative Linear Least Squares, Problem-Based.
Automatic differentiation (AD) applies to the solve and
prob2struct
functions under the following conditions:
The objective and constraint functions are supported, as described in Supported Operations for Optimization Variables and Expressions. They do not require use of the
fcn2optimexprfunction.The solver called by
solveisfmincon,fminunc,fsolve, orlsqnonlin.For optimization problems, the
'ObjectiveDerivative'and'ConstraintDerivative'name-value pair arguments forsolveorprob2structare set to'auto'(default),'auto-forward', or'auto-reverse'.For equation problems, the
'EquationDerivative'option is set to'auto'(default),'auto-forward', or'auto-reverse'.
| When AD Applies | All Constraint Functions Supported | One or More Constraints Not Supported |
|---|---|---|
| Objective Function Supported | AD used for objective and constraints | AD used for objective only |
| Objective Function Not Supported | AD used for constraints only | AD not used |
Note
For linear or quadratic objective or constraint functions, applicable solvers always use explicit function gradients. These gradients are not produced using AD. See Closed Form.
When these conditions are not satisfied, solve estimates gradients by
finite differences, and prob2struct does not create gradients in its
generated function files.
Solvers choose the following type of AD by default:
For a general nonlinear objective function,
fmincondefaults to reverse AD for the objective function.fmincondefaults to reverse AD for the nonlinear constraint function when the number of nonlinear constraints is less than the number of variables. Otherwise,fmincondefaults to forward AD for the nonlinear constraint function.For a general nonlinear objective function,
fminuncdefaults to reverse AD.For a least-squares objective function,
fminconandfminuncdefault to forward AD for the objective function. For the definition of a problem-based least-squares objective function, see Write Objective Function for Problem-Based Least Squares.lsqnonlindefaults to forward AD when the number of elements in the objective vector is greater than or equal to the number of variables. Otherwise,lsqnonlindefaults to reverse AD.fsolvedefaults to forward AD when the number of equations is greater than or equal to the number of variables. Otherwise,fsolvedefaults to reverse AD.
Note
To use automatic derivatives in a problem converted by prob2struct, pass options specifying these derivatives.
options = optimoptions('fmincon','SpecifyObjectiveGradient',true,... 'SpecifyConstraintGradient',true); problem.options = options;
Currently, AD works only for first derivatives; it does not apply to second or higher
derivatives. So, for example, if you want to use an analytic Hessian to speed your
optimization, you cannot use solve directly, and must instead use the
approach described in Supply Derivatives in Problem-Based Workflow.
Extended Capabilities
solve estimates derivatives in parallel for nonlinear solvers
when the UseParallel option for the solver is
true. For example,
options = optimoptions('fminunc','UseParallel',true); [sol,fval] = solve(prob,x0,'Options',options)
solve does not use parallel derivative estimation when all
objective and nonlinear constraint functions consist only of supported operations,
as described in Supported Operations for Optimization Variables and Expressions. In this case,
solve uses automatic differentiation for calculating
derivatives. See Automatic Differentiation.
You can override automatic differentiation and use finite difference estimates in
parallel by setting the 'ObjectiveDerivative' and 'ConstraintDerivative' arguments to
'finite-differences'.
When you specify a Global Optimization Toolbox solver that support parallel computation (ga (Global Optimization Toolbox), particleswarm (Global Optimization Toolbox), patternsearch (Global Optimization Toolbox), and surrogateopt (Global Optimization Toolbox)), solve compute in parallel when
the UseParallel option for the solver is true.
For example,
options = optimoptions("patternsearch","UseParallel",true); [sol,fval] = solve(prob,x0,"Options",options,"Solver","patternsearch")
Version History
Introduced in R2017bTo choose options or the underlying solver for solve, use
name-value pairs. For example,
sol = solve(prob,'options',opts,'solver','quadprog');
The previous syntaxes were not as flexible, standard, or extensible as name-value pairs.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Sélectionner un site web
Choisissez un site web pour accéder au contenu traduit dans votre langue (lorsqu'il est disponible) et voir les événements et les offres locales. D’après votre position, nous vous recommandons de sélectionner la région suivante : .
Vous pouvez également sélectionner un site web dans la liste suivante :
Comment optimiser les performances du site
Pour optimiser les performances du site, sélectionnez la région Chine (en chinois ou en anglais). Les sites de MathWorks pour les autres pays ne sont pas optimisés pour les visites provenant de votre région.
Amériques
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)