Optimiser la fonction à l'aide de particleswarm, basé sur les problèmes
Cet exemple montre comment minimiser une fonction en utilisant un essaim particulaire dans l'approche basée sur les problèmes lorsque l'objectif est un fichier de fonction, éventuellement de contenu inconnu (une fonction « boîte noire »). La fonction de minimisation, dejong5fcn(x), est incluse lorsque vous exécutez cet exemple.
dejong5fcn
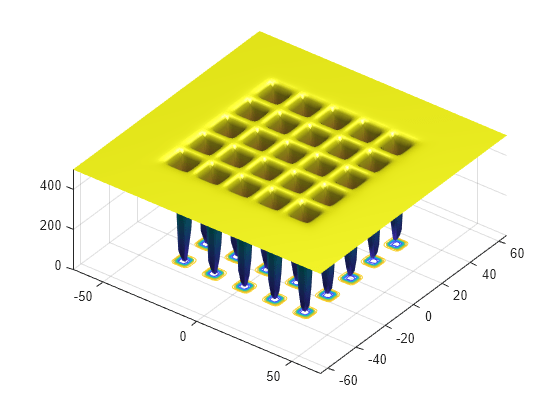
Créez une variable d’optimisation 2D x. La fonction dejong5fcn s'attend à ce que la variable soit un vecteur de ligne, spécifiez donc x comme un vecteur de ligne à 2 éléments.
x = optimvar("x",1,2);Pour utiliser dejong5fcn comme fonction objectif, convertissez la fonction en expression d'optimisation à l'aide de fcn2optimexpr.
fun = fcn2optimexpr(@dejong5fcn,x);
Créez un problème d’optimisation avec la fonction objectif fun.
prob = optimproblem("Objective",fun);Définissez des limites variables de –50 à 50 dans tous les composants. Lorsque vous spécifiez des limites scalaires, le logiciel étend les limites à toutes les variables.
x.LowerBound = -50; x.UpperBound = 50;
Résolvez le problème en spécifiant le solveur particleswarm.
rng default % For reproducibility [sol,fval] = solve(prob,"Solver","particleswarm")
Solving problem using particleswarm. Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
sol = struct with fields:
x: [-31.9751 -31.9719]
fval = 0.9980
Voir aussi
particleswarm | fcn2optimexpr | solve