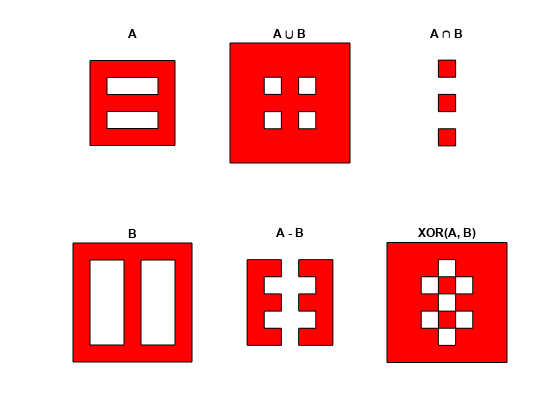
polybool
Set operations on polygonal regions
The polybool function is not recommended. Use a shape object and
the intersect,
union,
subtract, or
xor
function, instead. For more information, see Version History.
Description
[
performs the polygon set operation identified by x,y] =
polybool(flag,x1,y1,x2,y2)flag. The
result is output using the same format as the input. Geographic data that
encompasses a pole cannot be used directly. Use flatearthpoly to convert polygons that contain a pole to Cartesian
coordinates.
Most Mapping Toolbox™ functions adhere to the convention that individual contours with
clockwise-ordered vertices are external contours and individual contours with
counterclockwise-ordered vertices are internal contours. Although the
polybool function ignores vertex order, follow this
convention when creating contours to ensure consistency with other functions.
Examples
Input Arguments
Output Arguments
Tips
Numerical problems can occur when the polygons have a large offset from the origin. To avoid this issue, translate the coordinates to a location closer to the origin before performing the operation. Then, undo the translation after completing the operation. For example:
[x,y] = polybool(flag,x1-xt,y1-yt,x2-xt,y2-yt);x = x+xt;y = y+yt;