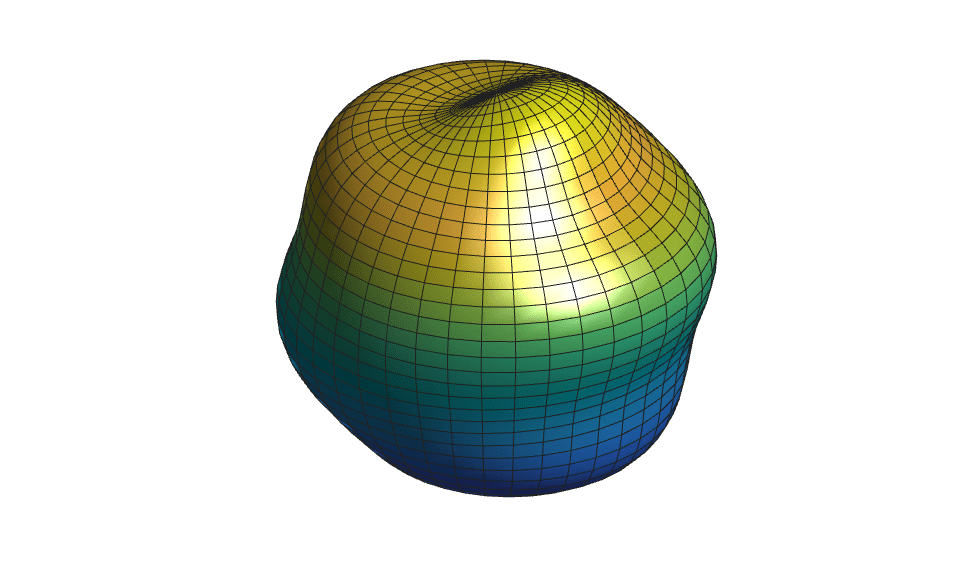
Animating a Surface
This example shows how to animate a surface. Specifically, this example animates a spherical harmonic. Spherical harmonics are spherical versions of Fourier series and can be used to model the free oscillations of the Earth.
Define the Spherical Grid
Define a set of points on a spherical grid to calculate the harmonic.
theta = 0:pi/40:pi; phi = 0:pi/20:2*pi; [phi,theta] = meshgrid(phi,theta);
Calculate the Spherical Harmonic
Calculate the spherical harmonic with a degree of six, an order of one, and an amplitude of 0.5 on the surface of a sphere with a radius equal to five. Then, convert the values to Cartesian coordinates.
degree = 6; order = 1; amplitude = 0.5; radius = 5; Ymn = legendre(degree,cos(theta(:,1))); Ymn = Ymn(order+1,:)'; yy = Ymn; for kk = 2: size(theta,1) yy = [yy Ymn]; end yy = yy.*cos(order*phi); order = max(max(abs(yy))); rho = radius + amplitude*yy/order; r = rho.*sin(theta); x = r.*cos(phi); y = r.*sin(phi); z = rho.*cos(theta);
Plot the Spherical Harmonic on the Surface of a Sphere
Using the surf function, plot the spherical harmonic on the surface of the sphere.
figure s = surf(x,y,z); light lighting gouraud axis equal off view(40,30) camzoom(1.5)
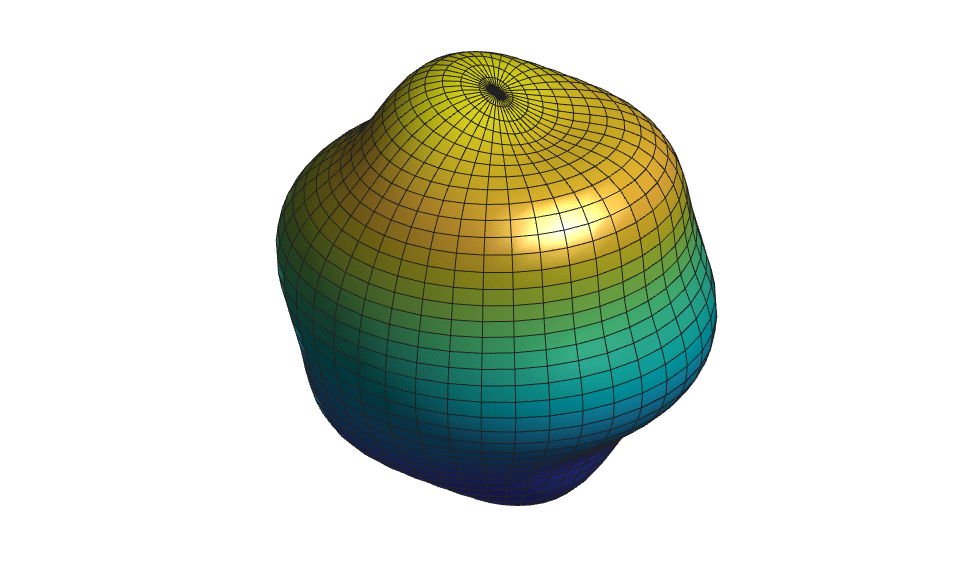
Animate the Surface
To animate the surface, use a for loop to change the data in your plot. To replace the surface data, set the XData, YData, and ZData properties of the surface to new values. To control the speed of the animation, use pause after updating the surface data.
scale = [linspace(0,1,20) linspace(1,-1,40)]; for ii = 1:length(scale) rho = radius + scale(ii)*amplitude*yy/order; r = rho.*sin(theta); x = r.*cos(phi); y = r.*sin(phi); z = rho.*cos(theta); s.XData = x; s.YData = y; s.ZData = z; pause(0.05) end